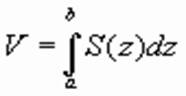Как Архимед находил объём шара

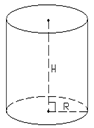
Рассмотрим прямоугольник размером 2R х 4R, круг, касающийся его длинных сторон в их серединах A и B, и треугольник, вписанный в него (рис. 1). При вращении вокруг оси АВ эти фигуры образуют цилиндр, шар и конус. Пересечём их плоскостью, проходящей параллельно основаниям цилиндра на расстоянии х от А. Обозначим площади сечений — будем называть их соответственными — через Sц, Sш и Sк. Тогда

x • Sц = 2R • (Sш + Sк). (*)

Действительно Sц = 4 R²; Sш = СЕ², где СЕ² = ЕО² - ОС² = R²-(х – R)² = 2Rх - х²; Sк = СD² = х², и равенство (*) проверяется прямой подстановкой. Если бы в его левой части вместо х стоял постоянный множитель, т. е. зависимость между тремя сечениями оставалась одной и той же для любой плоскости, то такое же равенство было бы верно и для объёмов Vц,Vш и Vк. Архимед нашёл чрезвычайно остроумный путь— объединил равенства (*) при разных х в одно соотношение для объёмов. Он посмотрел на уравнение (*) как на “правило рычага”: х и 2R он принял за плечи, а плоскости сечений — за массы. Его идею иллюстрирует рис. 2. На одно плечо рычажных весов, как на ось, надет цилиндр так, что точка А совпадает с точкой опоры; на другое плечо на расстоянии 2R от точки опоры подвешены конус и шар. Соответственные сечения цилиндра, конуса и шара уравновешивают друг друга, а значит, и весы в целом находятся в равновесии. Равновесие не нарушится, если сосредоточить всю массу цилиндра в его центре, расположенном на расстоянии R от опоры. Записываем правило рычага для всей системы, учитывая, что массы пропорциональны объёмам:

RVц = 2R(Vш+Vк).

Следовательно,

Vш =Vц/2 – Vк,

откуда легко вывести известную формулу объёма шара: Vш=4/3 R² (ВЫПИСАТЬ)

Архимед нашёл и другой способ вычисления объёма шара — по существу, очень близкий к интегрированию.

1) Объем шара равен объему пирамиды, основание которой имеет ту же площадь, что и поверхность шара, а высота есть радиус шара: Vш=4/3 R²

2) Площадь сферы (или поверхность шара) равна учетверенной площади большого круга: Sсферы=4 R²

А теперь составим уравнение сферы с центром А (a; b; c) и радиусом R в декартовой прямоугольной системе координат Oxyz.

Пусть M(x; y; z) – любая точка этой сферы. Тогда MA=R или MA²=R². Учитывая, что MA²=(x-a)²+(y-b⁾²+(z-c)², получаем искомое уравнение сферы

(x-a)² + (y-b)² + (z-c)² = R².

Тор – фигура вращения.

Тор образуется при вращении окружности вокруг не пересекающей её прямой, лежащей в плоскости окружности.

Если “заполнить” тор, то получится тело вращения, называемое полноторием.

1) Объем, ограниченный тором, равен произведению длины окружности на площадь поперечного сечения: V=2 R · r?=2 ²Rr²;

2) Площадь поверхности равна удвоенному произведению длины окружности на длину поперечного сечения: Sповерх=4 ²Rr

Интегральное исчисление, созданное Ньютоном и Лейбницем, превратило вычисление объемов в стандартную операцию. Она записывается следующей формулой:

где V – объем тела, расположенного между плоскостями z=a и z=b, а S(z) – площадь его сечения плоскостью, проходящей через точку z оси Oz перпендикулярно этой оси.

ПРОСМОТРЕТЬ ПРЕЗЕНТАЦИЮ

3. ВЫПОЛНИТЬ Д/З: Составить таблицу – справочник
                                           (нужна для практической работы)

Геометрическое тело  (рис)	Название	Формулы
	Цилиндр	S бок=2 π RH S полн= S бок+2 S осн= =2 π RH + 2 π R ^2 =2 π R (R + H) V= π R^2H

                               

Свойства объёмов