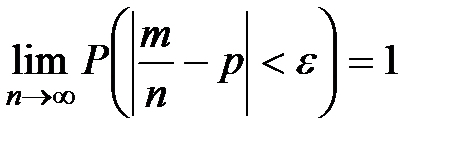Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дискретно распределённая случайная величина.
Закон распределения полностью характеризует случайные величины, но часто он неизвестен и приходится ограничиваться меньшими сведениями. Иногда выгоднее пользоваться числами, которые описывают случайные величины суммарно, такие числа наз. числовыми характеристиками случайных величин. Функцией распределения случайных величин называется функция F(x) действительной переменной х, определяющая вероятность того, что случайная величина Х примет в результате реализации эксперимента значение, меньшее, чем заданное х. Функция распределения F(x) случайной величины Х имеет следующие свойства: 1. Все значения функции распределения F(x) принадлежат отрезку [0, 1], т.е. 0≤ F(x) ≥1. 2. Функция распределения F(x) является неубывающей, т.е. если З. Функция F(x) в точке
4. Если все возможные значения случайной величины Х принадлежат интервалу (а, b), то для ее функции распределения F(x) F(x) = о при х≤ а, F(x) = 1 при х≥b.
Непрерывно распределённая случайная величина. Непрерыв. СВ-СВ которая может принимать все значения из некоторого конечного или бесконечного промежутков. Математическим ожиданием непрерывной случайной величины
Дисперсией непрерывной случайной величины
Среднее квадратичное отклонение непрерывной случайной величины
22. Плотность распределения непрерывной случайной величины -это (диферил. ф-цыя распределения) f(x), p(x) – наз первую производную от интервальной функции распределения. Свойства плотность распределения: 1. f(x)≥0, т.к. F(X)- возрастает 2. Р(а<x<в)= 3. Биномиальный закон распределения СВ. Биномиальное распределение -вероятностный закон последовательности независимых испытаний Бернулли. Математическое ожидание числа появления события А в п-независимых испытаниях равно произведению числа испытаний на вероятность появления соб.А в каждом из них М(х)=nq; Дисперсия числа появления соб.А в п-независимых испытаниях равна произведению числа испытаний на вероятность появления и непоявления соб.А D(х)=npq; Среднее квадратическое отклонение G=
ПР Найти М(х) и D(х) число бракованных изделий в партии из 1000 изделии. Если каждое изделие может оказаться бракованным с вероятностью 0,005 n=1000 p=0,005 g=0,995 М(х)=1000*0,005=5 D(х)=1000*0,005*0,995=4,975 Распределение Пуассона СВ. Если вероятность р события в каждом испытании при неограниченном увеличении числа испытаний n, изменяется т.о., что np= то вероятность того, что некоторое событие появится m раз в n испытаниях стремится к величине Рn(m) Закон распределения Пуассона: М(х)= D(х)= Έ= 26.Нормальный закон распределение СВ (распределение Гаусса). Случайная величина Х распределена по нормальному закону, если плотность распределения имеет вид: Р(х)= а=М(х)
Вер.попад.норм.распре-ной случ.вели-ны в интервал (α;β) вычисляется по формуле: P(α<x<β)=Ф( Для ее вычисления используются специальные таблицы или методы приближенного вычисления. 27. Геометрическое распределение случайной величины Неравенство Чебышева. Оценим вероятность отклонения СВ от ее мат ожидания по абсолютному значению, т.е. P{|X-M(X)|≥
Закон больших величин. Если 1) При достаточно большом числе п СВ имеющих 2) ограниченные дисперсии почти достоверно, что отклонение среднеарифметической СВ от среднеарифметического их мат ожидания будет сколь угодно мало по абсолютной величине. Без доказательства (на основании неравенства Чебышева). На практике СВ Хi имеет одно и тоже мат ожидание, равное а, тогда последнее неравенство можно представить в виде: Теорема Бернулли.
Если в каждой из п независимых испытаниях вероятность р появления события А постоянно, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности р по абсолютной величине будет сколь угодно малым, если число п достаточно велико:
|
||||||
|
Последнее изменение этой страницы: 2022-01-22; просмотров: 35; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.214.32 (0.01 с.) |
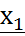 <
<  , то F(
, то F(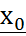 непрерывна слева, Т.е.
непрерывна слева, Т.е.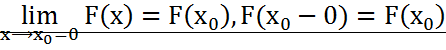

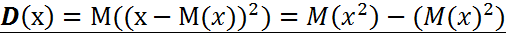
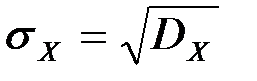
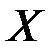 называется значение интеграла:
называется значение интеграла:
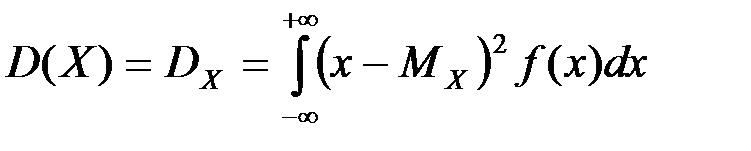 .
.

 .
.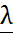 ,
, 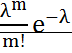 , т.е.
, т.е.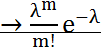 при n
при n 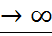 .
.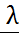
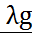
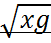
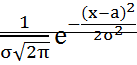 .
.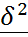 =Д(х)
=Д(х)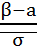 ) – Ф(
) – Ф(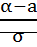 ). Функция Лапласа не выражается через элементарные функции
). Функция Лапласа не выражается через элементарные функции 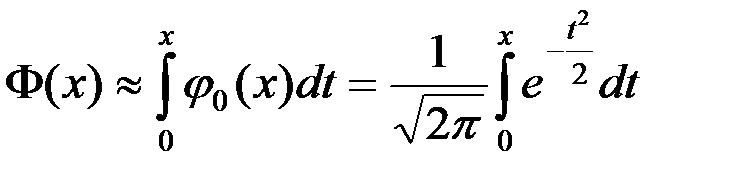 .
.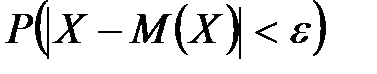 . Впервые это неравенство было доказано Чебышевым. Вероятность того, что отклонение СВ Х от ее мат ожидания меньше положительного числа ε не меньше, чем
. Впервые это неравенство было доказано Чебышевым. Вероятность того, что отклонение СВ Х от ее мат ожидания меньше положительного числа ε не меньше, чем 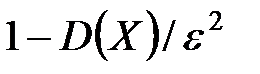 .
.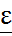 }≤
}≤ 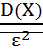 .
.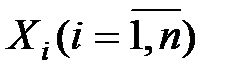 попарно независимы СВ, причем их дисперсия равномерно ограничены
попарно независимы СВ, причем их дисперсия равномерно ограничены 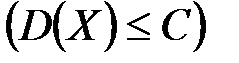 , где C=const, то как бы ни было мало положительное число ε вероятность неравенства
, где C=const, то как бы ни было мало положительное число ε вероятность неравенства 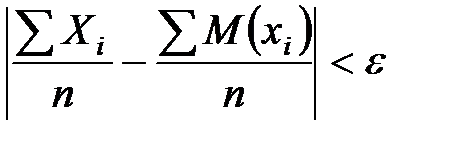 будет сколь угодно близка к единице, если число СВ достаточно велико:
будет сколь угодно близка к единице, если число СВ достаточно велико: 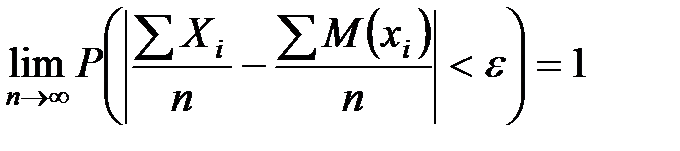 . Т.О. это означает:
. Т.О. это означает: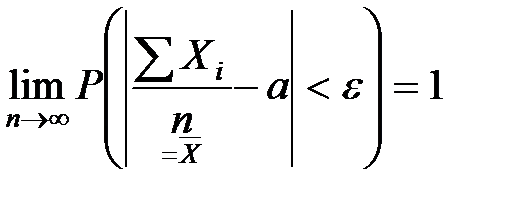 .
.