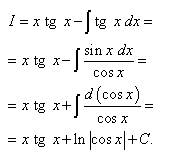Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применяем интегрирование по частям вместе ⇐ ПредыдущаяСтр 6 из 6
Пример 1. Найти неопределённый интеграл методом интегрирования по частям:
Решение. В подынтегральном выражении - логарифм, который, как мы уже знаем, разумно обозначить через u. Полагаем, что Тогда Находим (как уже говорилось в пояснении к теоретической справке, сразу же получаем в первом слагаемом (без интеграла) логарифмическую функцию, а во втором слагаемом (под знаком интеграла) - функцию, не содержащую логарифма):
И снова логарифм... Пример 2. Найти неопределённый интеграл:
Решение. Пусть Логарифм присутствует в квадрате. Это значит, что его нужно дифференцировать как сложную функцию. Находим, Применяя формулу интегрирования по частям, получаем:
Второй интеграл вновь находим по частям и получаем уже упомянутое преимущество (в первом слагаемом (без интеграла) логарифмическую функцию, а во втором слагаемом (под знаком интеграла) - функцию, не содержащую логарифма).
Находим изначальный интеграл:
Пример 3. Найти неопределённый интеграл методом интегрирования по частям:
Решение. Арктангенс, как и логарифм, лучше обозначить через u. Итак, пусть Тогда Применяя формулу интегрирования по частям, получаем:
Второй интеграл находим методом замены переменной.
Возвращаясь к переменной x, получаем
Находим изначальный интеграл:
Пример 4. Найти неопределённый интеграл методом интегрирования по частям:
находим
Пример 5. Найти неопределённый интеграл методом интегрирования по частям:
Решение. Пусть Используя формулу интегрирования по частям (1), находим:
Пример 6. Найти неопределённый интеграл методом интегрирования по частям:
Решение. Синус, как и экспоненту, удобно обозначить через dv. Пусть Тогда По формуле интегрирования по частям находим:
Пример 7. Найти неопределённый интеграл методом интегрирования по частям:
Решение. Косинус, как и синус и экспоненту, удобно обозначить через dv. Итак, Тогда По формуле интегрирования по частям находим:
Ко второму слагаемому вновь применяем интегрирование по частям. Обозначаем Тогда Интегрируя далее, находим:
Пример 8. Найти неопределённый интеграл методом интегрирования по частям:
Решение. Логарифм удобно обозначить через u. Итак, Тогда По формуле интегрирования по частям находим:
Пример 9. Найти неопределённый интеграл методом интегрирования по частям:
Решение. Обозначаем Тогда По формуле интегрирования по частям находим:
Ко второму слагаемому также применяем интегрирование по частям. Обозначаем Тогда Далее интегрируем:
Теперь из полученного уравнения выразим требуемый интеграл
и окончательно находим:
Пример 10. Найти неопределённый интеграл методом интегрирования по частям:
Решение. Как и во всех подобных случаях, косинус удобно обозначить через dv. Обозначаем Тогда По формуле интегрирования по частям получаем:
Ко второму слагаемому также применяем интегрирование по частям. Обозначаем Тогда Применив эти обозначения, интегрируем упомянутое слагаемое:
Теперь находим требуемый интеграл:
Среди интегралов, которые можно решить методом интегрирования по частям, есть и такие, которые не входят ни в одну из трёх упомянутых в теоретической части групп, относительно которых из практики известно, что лучше обозначать через u, а что через dv. Поэтому в этих случаях нужно пользоваться соображением удобства, также приведённым в параграфе "Суть метода интегрирования по частям": за u следует брать такую часть подынтегральной функции, которая при дифференцировании сильно не усложняется, а за dv - такую часть подынтегрального выражения, которая легко интегрируется. Последний пример этого урока - решение именно такого интеграла. Пример 11. Найти неопределённый интеграл методом интегрирования по частям:
Решение. Примем как руководство к действию общее соображение относительно обозначений. Обозначаем Тогда По формуле интегрирования по частям получаем:
|
|||||
|
Последнее изменение этой страницы: 2022-01-22; просмотров: 48; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.146.87 (0.021 с.) |
 .
. .
. .
.
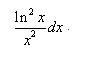 .
.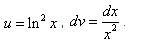 .
. .
.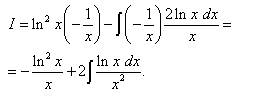
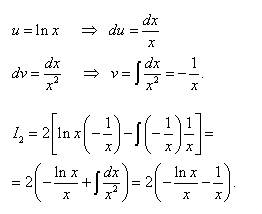
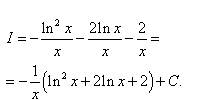
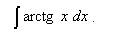 .
.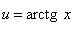 ,
, 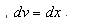 .
.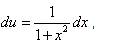 ,
, 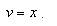 .
.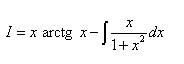
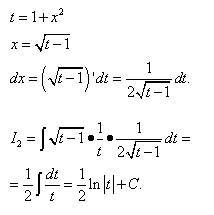
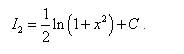 .
.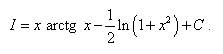 .
.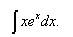
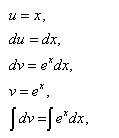
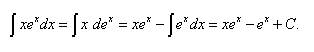
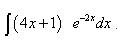 .
. . Тогда
. Тогда  .
.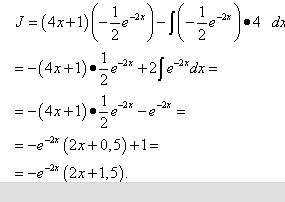
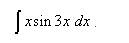 .
.
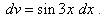 .
. .
.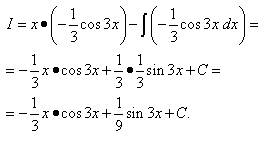
 .
. ,
, 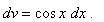 .
.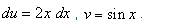 .
.
 .
.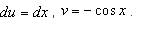 .
.
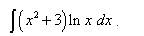 .
. .
.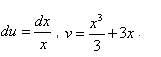 ,.
,.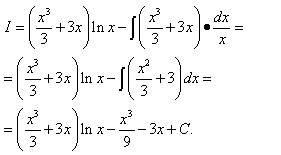
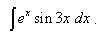 .
.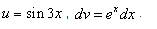 .
.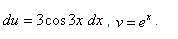 .
.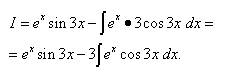
 .
.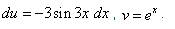 .
.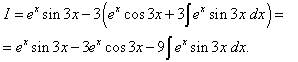
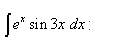 :
: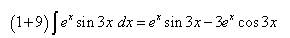
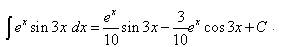 .
.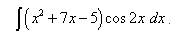 .
.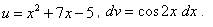 .
. .
.
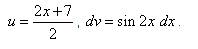 .
.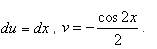 .
.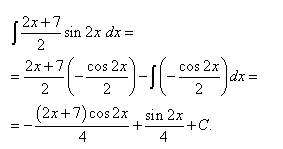
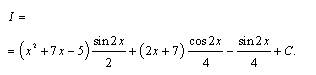
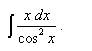 .
.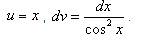 .
.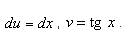 .
.