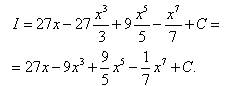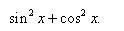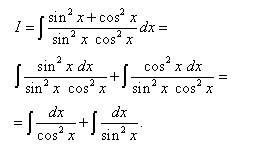Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Находим неопределённые интегралы вместе
Пример 1. Найти неопределённый интеграл
Решение. Видим в знаменателе подынтегрального выражения многочлен, в котором икс в квадрате. Это почти верный признак того, что можно применить табличный интеграл 21 (с арктангенсом в результате). Выносим из знаменателя множитель-двойку (есть такое свойство интеграла - постоянный множитель можно выносить за знак интеграла, выше оно было упомянуто как теорема 3). Результат всего этого:
Теперь в знаменателе сумма квадратов, а это значит, что можем применить упомянутый табличный интеграл. Окончательно получаем ответ:
Пример 2. Найти неопределённый интеграл
Решение. Вновь применяем теорему 3 - свойство интеграла, на основании которого постоянный множитель можно выносить за знак интеграла:
Применяем формулу 7 из таблицы интегралов (переменная в степени) к подынтегральной функции:
Сокращаем получившиеся дроби и перед нами конечный ответ:
Пример 3. Найти неопределённый интеграл
Решение. Применяя сначала теорему 4, а затем теорему 3 о свойствах, найдём данный интеграл как сумму трёх интегралов:
Все три полученные интеграла – табличные. Используем формулу (7) из таблицы интегралов при n = 1/2, n = 2 и n = 1/5, и тогда
где
объединяет все три произвольные постоянные, которые были введены при нахождении трёх интегралов. Поэтому в аналогичных ситуациях следует вводить только одну произвольную постоянную (константу) интегрирования. Пример 4. Найти неопределённый интеграл
Решение. Когда в знаменателе подынтегральной дроби - одночлен, можем почленно разделить числитель на знаменатель. Исходный интеграл превратился в сумму двух интегралов:
Чтобы применить табличный интеграл, преобразуем корни в степени и вот уже окончательный ответ:
Найти неопределённый интеграл самостоятельно, а затем посмотреть решение Пример 5. Найти неопределённый интеграл
Решение. Видим, что выражение подынтегральной функции содержит постоянный множитель 7, так как это выражение можно разделить на 7. Поэтому применяем правило, которое мы в теоретической части разобрали: выражение первообразной помножается на число, обратное постоянному множителю. Таким образом, выражение первообразной нужно помножить на 1/7. В свою очередь первообразная косинуса - это синус. Получаем:
Пример 6. Найти неопределённый интеграл
Решение. Видим, что выражение подынтегральной функции содержит постоянный множитель 2, так как это выражение можно разделить на 2. Поэтому применяем правило, которое мы в теоретической части разобрали: выражение первообразной домножается на число, обратное постоянному множителю. Таким образом, выражение первообразной нужно домножить на 1/2. В свою очередь первообразная синуса - это минус косинус. Получаем:
Пример 7. Найти неопределённый интеграл
Решение. Если мы преобразуем подынтегральную функцию, возведя двучлен в квадрат и разделив почленно числитель на знаменатель, то исходный интеграл станет суммой трёх интегралов:
(мы применили обе нужные нам на этом уроке теоремы о свойствах интеграла). Все полученные интегралы – табличные. Используем формулу (7) из таблицы интегралов при n = 2/3, n = 7/6, n = 5/3 и за последним знаком равенства - окончательное решение.
Пример 8. Найти неопределённый интеграл
Решение. В подынтегральном выражении нужно умножить многочлен на одночлен, тогда получим сумму двух интегралов:
Применяем табличный интеграл, интегрируя степенные функции, и окончательный ответ:
Пример 9. Найти неопределённый интеграл
Решение. В подынтегральном выражении - многочлен в степени. Возведём его в степень и получим сумму интегралов, в которой постоянные множители вынесены за знаки интеграла:
Интегрируем каждое слагаемое и перед нами - окончательный ответ:
Пример 10. Найти неопределённый интеграл
Решение. Представим числитель подынтегральной функции, равный 1, в виде
Тогда
Оба интеграла – табличные. Используя формулы (17) и (18) из таблицы интегралов, получим
|
|||||
|
Последнее изменение этой страницы: 2022-01-22; просмотров: 43; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.109.211 (0.008 с.) |
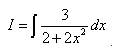 .
.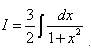
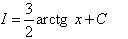 .
. .
.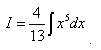 .
.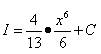 .
.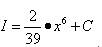 .
.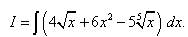

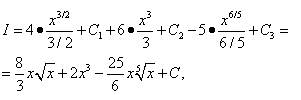
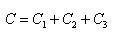
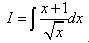 .
.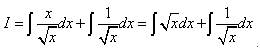 .
.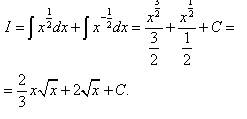
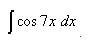
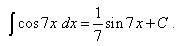

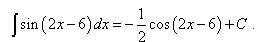

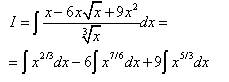

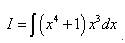 .
.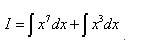 .
. .
.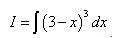 .
.