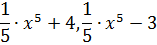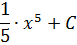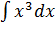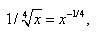Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Первообразная функция и неопределённый интегралСтр 1 из 6Следующая ⇒
Геометрический смысл неопределённого интеграла Пусть требуется найти кривую y=F(x) и мы уже знаем, что тангенс угла наклона касательной в каждой её точке есть заданная функция f(x) абсциссы этой точки. Согласно геометрическому смыслу производной, тангенс угла наклона касательной в данной точке кривой y=F(x) равен значению производной F'(x). Значит, нужно найти такую функцию F(x), для которой F'(x)=f(x). Требуемая в задаче функция F(x) является первообразной от f(x). Условию задачи удовлетворяет не одна кривая, а семейство кривых. y=F(x) - одна из таких кривых, а всякая другая кривая может быть получена из неё параллельным переносом вдоль оси Oy. Назовём график первообразной функции от f(x) интегральной кривой. Если F'(x)=f(x), то график функции y=F(x) есть интегральная кривая. Факт 3. Неопределённый интеграл геометрически представлен семеством всех интегральных кривых, как на рисунке ниже. Удалённость каждой кривой от начала координат определяется произвольной постоянной (константой) интегрирования C.
Свойства неопределённого интеграла Факт 4. Теорема 1. Производная неопределённого интеграла равна подынтегральной функции, а его дифференциал – подынтегральному выражению. Факт 5. Теорема 2. Неопределённый интеграл от дифференциала функции f (x) равен функции f (x) с точностью до постоянного слагаемого, т.е.
Теоремы 1 и 2 показывают, что дифференцирование и интегрирование являются взаимно-обратными операциями. Факт 6. Теорема 3. Постоянный множитель в подынтегральном выражении можно выносить за знак неопределённого интеграла, т.е.
Факт 7. Теорема 4. Неопределённый интеграл алгебраической суммы конечного числа функций равен алгебраической сумме неопределённых интегралов этих функций, т.е.
Таблица основных неопределённых интегралов Факт 8. Пользусь таблицей неопределённых интегралов, свойствами неопределённого интеграла и методами интегрирования, можно отыскать неопределённый интеграл любой функции. Из определения неопределённого интеграла вытекают следующие формулы, которые в дальнейшем будем называть табличными интегралами: (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) (24) (25) Метод замены переменной обычно применяется, когда подынтегральное выражение представляет собой независимую переменную, умноженную на многочлен от этой переменной, или на тригонометрическую функцию от этой переменной или на степенную функцию (в том числе корень) от этой переменной.
Пример 1. Найти неопределённый интеграл методом замены переменной:
Решение. Производим замену x − 1 = t; тогда x = t + 1. Отсюда dx = dt. По формуле (1)
Возвращаясь к переменной x, окончательно получаем
Пример 2. Найти неопределённый интеграл методом замены переменной:
Решение. Положим
Возвращаясь к переменной x, окончательно получаем
Если трудно уследить, куда в процессе решения примера 2 делись Пример 3. Найти неопределённый интеграл методом замены переменной:
Решение. Положим Тогда Заменяем переменную и получаем:
где степени при t складываются. Продолжаем преобразования и получаем:
Приводим дроби к общему знаменателю и возвращаемся к переменной x. Решаем и получаем ответ:
Применить замену переменной самостоятельно, а затем посмотреть решение Пример 4. Найти неопределённый интеграл методом замены переменной:
Решение. Сделаем подстановку Заменяем переменную и получаем:
Пример 5. Найти неопределённый интеграл методом замены переменной:
Решение. Полагаем Заменяем переменную и получаем:
Пример 6. Найти неопределённый интеграл методом замены переменной:
Решение. Полагаем Заменяем переменную и получаем:
Пример 7. Найти неопределённый интеграл методом замены переменной:
Решение. Положим
Тогда Заменяем переменную и получаем:
Возвращаясь к переменной х, получаем ответ:
Пример 8. Найти неопределённый интеграл методом замены переменной:
Решение. Положим Заменяем переменную и получаем:
Подставляя вместо t его выражение через x получаем ответ:
Пример 9. Найти неопределённый интеграл методом замены переменной:
Решение. Положим Заменяем переменную и получаем:
Решение с переменной t получено с использованием формулы 21 из таблицы интегралов. Подставляя вместо t его выражение через x получаем ответ:
Первообразная функция и неопределённый интеграл Факт 1. Интегрирование - действие, обратное дифференцированию, а именно, восстановление функции по известной производной этой функции. Восстановленная таким образом функция F (x) называется первообразной для функции f (x). Определение 1. Функция F (x) называется первообразной для функции f (x) на некотором промежутке X, если для всех значений x из этого промежутка выполняется равенство F '(x)= f (x), то есть данная функция f (x) является производной от первообразной функции F (x).. Например, функция F (x) = sin x является первообразной для функции f (x) = cos x на всей числовой прямой, так как при любом значении икса (sin x)' = (cos x). Определение 2. Неопределённым интегралом функции f (x) называется совокупность всех её первообразных. При этом употребляется запись ∫ f (x) dx, где знак ∫ называется знаком интеграла, функция f (x) – подынтегральной функцией, а f (x) dx – подынтегральным выражением. Таким образом, если F (x) – какая-нибудь первообразная для f (x), то ∫ f (x) dx = F (x) + C, (1) где C - произвольная постоянная (константа). В части задач на нахождение неопределённого интеграла даны такие подынтегральные функции, которые без особых услилий могут быть проинтегрированы непосредственно, то есть по таблице неопределённых интегралов. В задачах посложнее подынтегральную функцию нужно предварительно преобразовать так, чтобы можно было использовать табличные интегралы. Факт 2. Восстанавливая функцию как первообразную, мы должны учитывать произвольную постоянную (константу) C, а чтобы не писать список первообразной с различными константами от 1 до бесконечности, нужно записывать множество первообразных с произвольной константой C, например, так: 5 x ³+С. Итак, произвольная постоянная (константа) входит в выражение первообразной, поскольку первообразная может быть функцией, например, 5 x ³+4 или 5 x ³+3 и при дифференцировании 4 или 3, или любая другая константа обращаются в нуль. Поставим задачу интегрирования: для данной функции f ( x ) найти такую функцию F ( x ), производная которой равна f ( x ). Пример 1. Найти множество первообразных функции
Решение. Для данной функции первообразной является функция
так как
Функция F (x) называется первообразной для функции f (x), если производная F (x) равна f (x), или, что одно и то же, дифференциал F (x) равен f (x) dx, т.е.
или
Следовательно, функция
и вообще
где С – произвольная постоянная. В этом можно убедиться дифференцированием. Таким образом, если для функции существует одна первообразная, то для неё существует бесконечное множество первообразных, отличающихся на постоянное слагаемое. Все первообразные для функции записываются в приведённом выше виде. Это вытекает из следующей теоремы. Теорема (формальное изложение факта 2). Если F (x) – первообразная для функции f (x) на некотором промежутке Х, то любая другая первообразная для f (x) на том же промежутке может быть представлена в виде F (x) + C, где С – произвольная постоянная.
В следующем примере уже обращаемся к таблице интегралов, которая будет дана в ниже, после свойств неопределённого интеграла. Делаем это до ознакомления со всей таблицей, чтобы была понятна суть вышеизложенного. А после таблицы и свойств будем пользоваться ими при интегрировании во всей полноте. Пример 2. Найти множества первообразных функций: 1) 2) 3) Решение. Находим множества первообразных функций, из которых "сделаны" данные функции. При упоминании формул из таблицы интегралов пока просто примите, что там есть такие формулы, а полностью саму таблицу неопределённых интегралов мы изучим чуть дальше. 1) Применяя формулу (7) из таблицы интегралов при n = 3, получим
2) Используя формулу (10) из таблицы интегралов при n = 1/3, имеем
3) Так как
то по формуле (7) при n = -1/4 найдём
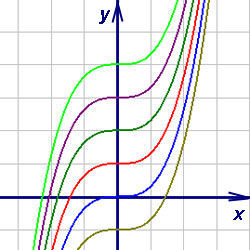
Под знаком интеграла пишут не саму функцию f, а её произведение на дифференциал dx. Это делается прежде всего для того, чтобы указать, по какой переменной ищется первообразная. Например,
здесь в обоих случаях подынтегральная функция равна, но её неопределённые интегралы в рассмотренных случаях оказываются различными. В первом случае эта функция рассматривается как функция от переменной x, а во втором - как функция от z. Процесс нахождения неопределённого интеграла функции называется интегрированием этой функции.
|
|||||||
|
Последнее изменение этой страницы: 2022-01-22; просмотров: 49; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.204.8 (0.069 с.) |
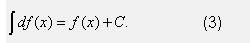
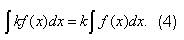
 (5)
(5)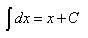
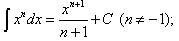
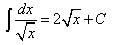
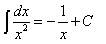
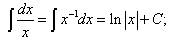
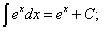
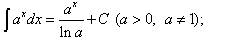
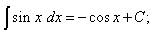

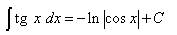
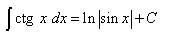

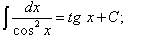
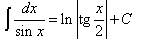
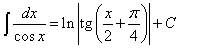

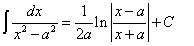
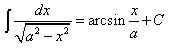

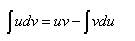



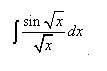 .
.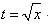 . Отсюда
. Отсюда 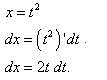 .
. 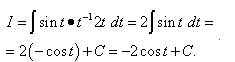 .
.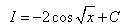
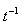 и
и 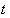 , это признак того, что нужно повторить действия со степенями из элементарной (школьной) математики.
, это признак того, что нужно повторить действия со степенями из элементарной (школьной) математики.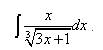 .
.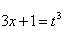 , откуда
, откуда 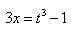 и
и  .
.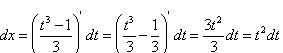 , в свою очередь
, в свою очередь  .
.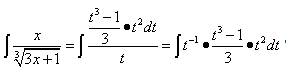 ,
,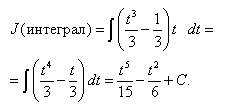
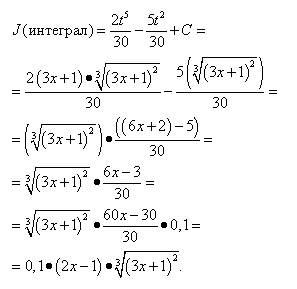
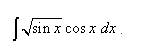
 , тогда
, тогда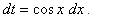 .
.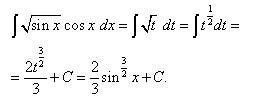
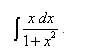 .
.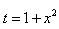 , тогда
, тогда 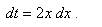 .
.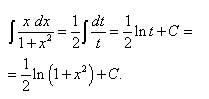
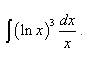 .
.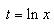 , тогда
, тогда 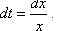 .
.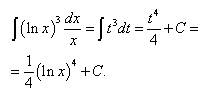
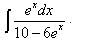 .
.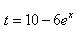 , откуда
, откуда 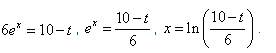 .
.
 .
. .
.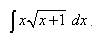 .
.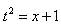 , откуда
, откуда  .
.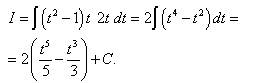
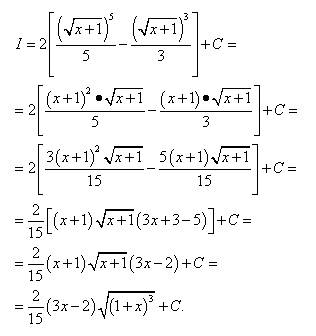
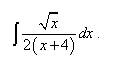 .
.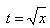 , тогда
, тогда 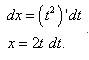 .
.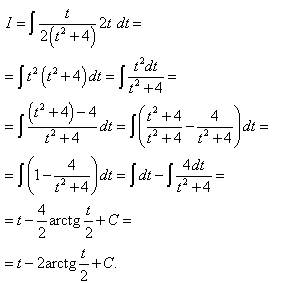
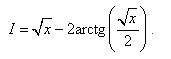

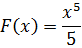
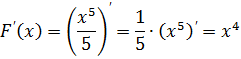
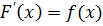
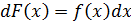 (2)
(2)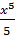 - первообразная для функции
- первообразная для функции  . Однако она не является единственной первообразной для
. Однако она не является единственной первообразной для