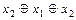Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Полнота и базис в булевой алгебре.
Система F:={ Функция
Определим предварительно 5 классов булевых функций (классов Поста). 1. Классом 2. Классом 3. Классом L линейных булевых функций L:={ где Коэффициенты
Проверка линейности сводится к нахождению коэффициентов
Пример 1. Проверим, является ли линейной функция Имеем Линейность булевой функции определить и другим способом – с помощью полинома Жегалкина 1–й степени от n переменных:
Полином Жегалкина называется нелинейным (линейным), если он содержит (не содержит) произведения переменных, т.е. линейность булевой функции равносильна линейности соответствующего полинома Жегалкина. Для получения полинома Жегалкина булевой функции используются аксиомы булевой алгебры и вспомогательные равенства: x Ú y = x Å y Å xy, x (y Å z)= xy Å xz, Пример 2. Определить, будет ли линейной функция: f (x, y, z)= Имеем Полученный полином Жегалкина является нелинейным, и, следовательно, функция f также нелинейна. 4. Классом S самодвойственных булевых функций S:={ 5. Классом M монотонных булевых функций
Пример 3. Определим, к каким классам Поста относится булева функция
1. f (0,0)=1, т.е. f (x, y)Ï 2. f (1,1)=0, т.е. f (x, y)Ï
4. f (0,0)> f (1,1), т.е. f (x, y)Ï M. 5. f (x, y)=1Å xy, т.е. f (x, y)Ï L.
Отметим, что каждый класс Поста замкнут относительно операций замены переменных и суперпозиций, т.е. с помощью этих операций из функций, принадлежащих данному классу, можно получить только функции из этого же класса. Для установления полноты системы S:={ Система F:={ В силу критерия полноты функция f (x, y) Система булевых функций F:={ Примеры всех 17 базисов в
Наиболее хорошо изученным является базис {&,Ú,Ø}.
Теорема 1.4.1. Каждый базис содержит не более четырех булевых функций. Для доказательства функциональной полноты предъявленной системы F:={ Теорема 1.4.2. Если все функции функционально полной системы å* представимы формулами над å, то å также функционально полна.
Пример 4. В алгебре Жегалкина (
Чтобы выяснить функциональную полноту системы å={&,Å,1}, достаточно показать, что через операции å можно выразить операции булевого базиса å*={&,Ú,Ø}: 1) 2) Построенные таблицы истинности (табл. 1.4.1 и 1.4.2) подтверждают справедливость формул 1) и 2).
Таблица 1.4.1
| ||||||||
 x x
| x | 1 | x Å1 | ||||||
| 0 | 1 | 1 | 1 | ||||||
| 1 | 0 | 1 | 0 | ||||||
|
Таблица 1.4.2 | |||||
| x 1 | x 2 | x 1Ú x 2 | x 1× x 2 | x 1× x 2Å x 1 | x 1× x 2Å x 1Å x 2 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 | 1 |
Вопросы для самопроверки и упражнения.
1. Функциональной полнотой обладают “усеченные” наборы булевых операций {&,Ú,Ø}: а) {&,Ø}; б){Ú,Ø}.
Для подтверждения их функциональной полноты достаточно выразить базис {&,Ú,Ø} через функции {&,Ø}, {ÚØ}. Проверить справедливость относительно “недостающих” операций:

 а)
а) 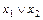 =
= 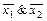 ; б)
; б)  &
&  =
= 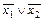 .
.
2. Показать (используя результаты упражнения 1):
1) базис {&,Ø} представим через базис Шеффера {|}:
а) 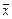 = x | x, б)
= x | x, б)  &
&  =(
=( |
|  ) | (
) | ( |
|  ).
).
2) базис {Ú,Ø} представим через базис Пирса {¯}:
а) 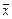 = x ¯ x, б)
= x ¯ x, б) 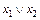 =(
=( ¯
¯  )¯ (
)¯ ( ¯
¯  ).
).
3. Показать, что ниже перечисленные функционально полные системы являются базисами:



 1. {®,~}, 2. {®,○}, 3. {®,®}, 4. {®,Å}, 5. {®,Ø}, 6. {®,Ø}, 7. {®,1}, 8. {~,&,○}, 9. {~,Ú,○}, 10. {Å,&,~}, 11. {Å,Ú,~}, 12. {Å,Ú,1}.
1. {®,~}, 2. {®,○}, 3. {®,®}, 4. {®,Å}, 5. {®,Ø}, 6. {®,Ø}, 7. {®,1}, 8. {~,&,○}, 9. {~,Ú,○}, 10. {Å,&,~}, 11. {Å,Ú,~}, 12. {Å,Ú,1}.
1.5. Эквивалентные преобразования.
1. Правило подстановки формулы F вместо переменной x.
2. Правило замены подформул. Если какая–либо формула F, описывающая функцию f, содержит 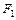 в качестве подформулы, то замена
в качестве подформулы, то замена 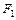 на эквивалентную
на эквивалентную 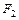 (
(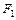 =
= 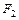 ) не изменит функции f; полученная при такой замене новая формула F ¢ эквивалентна исходной F.
) не изменит функции f; полученная при такой замене новая формула F ¢ эквивалентна исходной F.
Эквивалентные преобразования – преобразования, использующие эквивалентные соотношения и правило замены.
Основные эквивалентные соотношения (законы) в булевой алгебре:
1. Ассоциативность:
а)  ×(
×( ×
×  )
)  (
( ×
×  )×
)× 

 ×
×  ×
×  ;
;
б) 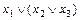

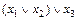

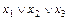 .
.
2. Коммутативность:
а)  ×
× 

 ×
×  ; б)
; б) 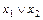

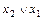 .
.
3. Дистрибутивность:
а)  ×(
×(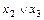 )
) 
 ×
× 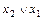 ×
×  ; б)
; б)  Ú(
Ú( ×
×  )=(
)=(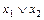 )×(
)×(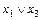 ).
).
4. Идемпотентность: а) x × x  x; б) x Ú x
x; б) x Ú x  x.
x.
5. Закон двойного отрицания: 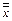
 x.
x.
6. Свойства констант 0 и 1:
а) x ×1  x; б) x Ú 1
x; б) x Ú 1 
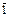 ; в)
; в) 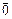
 1;
1;
г) x ×0  0; д) x Ú 0
0; д) x Ú 0 
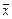 ; е)
; е) 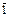
 0.
0.
7. Законы де Моргана:

 а)
а) 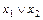

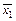 ×
× 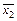 ; б)
; б)  ×
× 

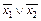 .
.
8. Закон противоречия: x × 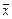
 0.
0.
9. Закон исключенного третьего: 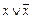
 1.
1.
Другие соотношения, часто применяемые в преобразованиях булевых формул, выводимы с помощью основных законов. Рассмотрим некоторые задачи эквивалентных преобразований в булевой алгебре и способы их решения.
1. Упрощение формул. Для упрощения формул используются следующие эквивалентные соотношения, выводимые из основных с помощью эквивалентных преобразований:
а) x Ú x × y  x, б) x ×(x Ú y)
x, б) x ×(x Ú y)  x – поглощение; (10)
x – поглощение; (10)
x × y Ú x × 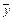
 x – склеивание; (11)
x – склеивание; (11)
x ×z Ú y × 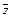 Ú x × y
Ú x × y  x ×z Ú y ×
x ×z Ú y × 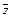 – обобщенное склеивание; (12)
– обобщенное склеивание; (12)
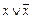 × y
× y  x Ú y. (13)
x Ú y. (13)
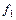 ,...,
,..., 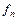 } называется полной в
} называется полной в 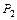 , если любая функция f Î
, если любая функция f Î 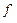 (
( ) называется суперпозицией функций
) называется суперпозицией функций 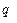 (
(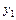 ,...,
,..., 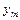 ) и
) и 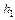 (
(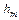 (
(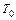 булевых функций
булевых функций 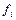 (
(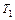 булевых функций
булевых функций 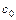 Å
Å 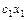 Å
Å 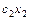 Å...Å
Å...Å 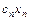 }
}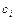 Î{0,1}, i =
Î{0,1}, i = 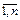 .
.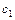 ,..,
,.., 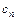 линейной функции
линейной функции 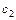 = 0 Å (0 Ú 1) = 1. Таким образом,
= 0 Å (0 Ú 1) = 1. Таким образом, 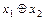 . Сопоставляя таблицы истинности формул
. Сопоставляя таблицы истинности формул 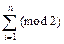
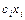 Å
Å 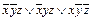 .
.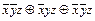
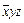 )Ú
)Ú 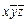 =
= 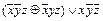 =
= 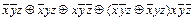 =
= 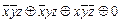 =
= 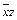 (
(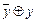 )
) 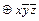 =
= 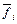 (
(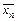 )}.
)}.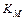 :={
:={ 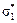 ,...,
,..., 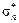 )³(
)³(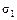 ,...,
,..., 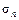 )Û(
)Û(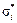 ³
³ 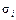 , i =
, i =  3. f (1,0)¹ f (0,1), т.е. f (x, y)Ï S.
3. f (1,0)¹ f (0,1), т.е. f (x, y)Ï S.
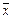 =
= 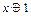 ,
,