
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные схемы логически правильных рассуждений.Стр 1 из 6Следующая ⇒
Оглавление Предисловие 4
1. Логика высказываний 5 1.1. Основные понятия 5 1.2. Основные схемы логически правильных рассуждений 8 1.3. Алгебра логики 11 1.4. Булева алгебра 14 1.5. Эквивалентные преобразования 18 1.6. Булева алгебра и теория множеств 27 2. Логика предикатов 35 2.1. Основные понятия 35 2.2. Кванторы 37 2.3. Выполнимость и истинность 39 2.4. Эквивалентные соотношения 42 3. Вопросы коллоквиума “Введение в математическую логику” 47
Список литературы 49
Предисловие
Настоящее методическое пособие призвано восполнить имеющийся пробел в учебной литературе по курсу “Дискретная математика”, в частности – практикум в решении задач по математической логике. Рассматриваются традиционные разделы: логика высказываний и логика предикатов. Используются теоретические сведения справочного характера, содержащие компактное изложение известных результатов, достаточные для демонстрации имеющихся методов решения рассматриваемых задач. Анализ разнообразной по уровню изложения современной учебной литературы по математической логике позволил указать наиболее удачные первоисточники как в подборе задач, так и демонстрации методов их решения. Материал практикума предоставляет возможность студентам самостоятельно освоить основные положения курса “Дискретная математика” (Ч. II. Введение в математическую логику), приобрести и закрепить практические навыки решения задач.
Пособие включает задачи для практических занятий, расчетно-графических работ и самостоятельного изучения элементов математической логики. Практикум строится как решебник, в котором подробный разбор многочисленных примеров преследует главную цель – достичь усвоения базовых понятий языка математической логики; последний рассматривается при этом как средство формулировки этих понятий (а не как набор формул и методов в решении задач).
1. ЛОГИКА ВЫСКАЗЫВАНИЙ. [1] Основные понятия. Современная математическая логика включает два основных раздела: логику высказываний и охватывающую ее логику предикатов, для построения которых существуют два подхода (языка), образующих два варианта формальной логики: алгебру логики и логические исчисления. Между основными понятиями этих языков формальной логики имеет место взаимно однозначное соответствие (изоморфизм). Высказывание – повествовательное предложение (суждение), о котором имеет смысл говорить, что оно истинно или ложно. Высказывание называется простым (элементарным), если оно рассматривается как некое неделимое целое. Сложным (составным) называется высказывание, составленное из простых с помощью логических связок. Основные логические связки (операции) логики высказываний определяются таблицами истинности. Пусть P, Q Î{ и,л }, где P, Q – простые высказывания, принимающие одно из двух значений: и – “истина”, л – “ложь”.
Таблица 1.1.1 | |||||
| P | Ø P | |||||
| и | л | |||||
| л | и | |||||
Ø P (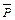 ) – отрицание (инверсия) высказывания P.
) – отрицание (инверсия) высказывания P.
|
Таблица 1.1.2 | ||||||
| P | Q | P & Q | P Ú Q | P ® Q | P ~ Q | P Å Q |
| л | л | л | л | и | и | л |
| л | и | л | и | и | л | и |
| и | л | л | и | л | л | и |
| и | и | и | и | и | и | л |
| 1 | 2 | 3 | 4 | 5 | ||
1) P & Q (P Ù Q, P × Q) – конъюнкция (операция “и”, логическое произведение) высказываний P, Q;
2) P Ú Q – дизъюнкция (операция “или”, логическое сложение) высказываний P, Q;
3) P ® Q (P É Q) – импликация (логическое следование) высказываний P, Q (читается: “если P, то Q ”);
|
|
4) P ~ Q (P º Q, P «Q) – эквивалентность (эквиваленция, равнозначность) высказываний P, Q (читается: “ P, если и только, если Q ”);
5) P Å Q (P ∆ Q) – неравнозначность (сложение по mod 2) высказываний P, Q (читается: “либо P, либо Q ”; “или P, или Q ”).
Выражение, составленное из обозначений высказываний, логических связок (и, возможно, скобок), назовем логической формулой, если оно удовлетворяет следующим условиям:
– переменная, обозначающая высказывание, – элементарная (атомарная) формула;
– если P и Q – формулы, то (P & Q), (P Ú Q), (Ø P), (P ® Q), (P ~ Q), (P Å Q) – формулы;
– других формул нет.
Пример 1. Записать логическими формулами следующие сложные высказывания:
1. “Если допоздна работаешь с компьютером и при этом пьешь много кофе, то утром просыпаешься в дурном расположении духа или с головной болью”.
2. “Если социологические исследования показывают, что потребитель отдает предпочтение удобству и многообразию выбора, то фирме следует сделать упор на усовершенствование товара или увеличение многообразия новых форм”.
Сравнить логические формулы и сделать выводы.
1. Первое составное высказывание состоит из следующих простых:
X – “Допоздна работаешь с компьютером”.
Y – “Пьешь много кофе”.
Z – “Утром встаешь в дурном расположении духа”.
U – “Утром встаешь с головной болью”.
Тогда логическая формула первого составного высказывания:
(X & Y)®(Z Ú U)
2. Второе составное высказывание состоит из следующих простых:
X – “Социологические исследования показывают, что потребитель отдает предпочтение удобству”.
Y – “Социологические исследования показывают, что потребитель отдает предпочтение многообразию выбора”.
Z – “Фирме следует сделать упор на усовершенствование товара”.
U – “Фирме следует сделать упор на увеличение многообразия новых форм”.
Логическая формула второго составного высказывания:
(X & Y)®(Z Ú U).
Как видим, оба составных высказывания описываются одной и той же формулой, хотя имеют различное содержание.
Пример 2. Записать формулами логики высказываний два способа доказательства равенства множеств, вытекающих из определений 1 и 2 равенства множеств X, Y.
Определение 1. “ X = Y, если из того, что a Î X, следует a Î Y, и из того, что a Ï X, следует, что a Ï Y ”.
Определение 2. “ X = Y, если из того, что a Î X, следует a Î Y, и из того, что a Î Y, следует, что a Î X ”.
Обозначим простые высказывания:
A:=“ a Î X ”;
B:=“ a Î Y ”;
C:=“ X = Y ”.
Тогда процедура доказательства X = Y:
а) для определения 1: ((A ® B)&(Ø A ®Ø B))®C;
б) для определения 2: ((A ® B)&(B ® A))®C;
Вопросы для самопроверки и упражнения.
1. Исходя из определения логической формулы, определить, являются ли формулами следующие выражения:
а) (((A Ú B)®Ø C) ~ D)&((A Å C)®Ø D).
б) ((A ÅØ B)® C) ~ (D &® B).
2. Записать логической формулой следующий текст:
“Если компьютер при запуске не выдает ошибку при проверке оперативной памяти, то она исправна. Если при запуске он выдает ошибку при проверке оперативной памяти и память установлена правильно, то либо оперативная память дефектна, либо дефектна материнская плата. Тогда если эта оперативная память установлена в другой (контрольный) компьютер и он при запуске не выдает ошибку при проверке оперативной памяти, то оперативная память исправна”.
|
|
3. Записать логической формулой следующую пословицу:
“Не ел – не мог, поел – без ног”.
4. Составить таблицы Кэли для основных логических связок – бинарных логических операций.
Вопросы для самопроверки и упражнения.
1. К каким схемам рассуждений относятся следующие рассуждения:
а) “Если рабочий отсутствовал на работе, он не выполнил задания. Он отсутствовал на работе. Следовательно, он не выполнил задания.”
б) “Идет дождь или снег. Идет дождь. Следовательно, не идет снег.”
Являются ли данные рассуждения логически правильными?
2. Записать логической формулой следующие умозаключения и уточнить их справедливость:
а) “Если капиталовложения останутся постоянными, то возрастут правительственные расходы или возникнет безработица. Если правительственные расходы не возрастут, то налоги будут снижены. Если налоги будут снижены и капиталовложения останутся постоянными, то безработица не возрастет. Следовательно, правительственные расходы возрастут.”
б) “Если Джонс не встречал этой ночью Смита, то либо Смит был убийцей, либо Джонс лжет. Если Смит не был убийцей, то Джонс не встречал Смита этой ночью, и убийство имело место после полуночи. Если убийство имело место после полуночи, то либо Смит был убийцей, либо Джонс лжет. Следовательно, Смит был убийцей.”
Алгебра логики.
Алгебра логики изучает строение сложных логических высказываний (логических формул) и способы установления их истинности с помощью алгебраических методов.
Каждая формула алгебры логики задает логическую функцию – функцию от логических переменных.
Алгебра логики – алгебра, образованная множеством B ={0,1} вместе со всеми возможными операциями на нем.
Функцией алгебры логики (или логической функцией) f ( ,...,
,...,  ) называется n–арная логическая операция на B, т.е. f:
) называется n–арная логическая операция на B, т.е. f: 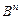 ® B. Множество всех логических функций (логических операций) обозначается
® B. Множество всех логических функций (логических операций) обозначается 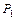 , |
, | 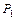 |=
|= 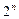 , множество всех логических операций n переменных –
, множество всех логических операций n переменных – 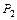 (n), |
(n), | 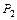 (n)|=
(n)|= 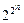 .
.
Любую логическую функцию f ( ,...,
,...,  ) можно задать таблицей истинности.
) можно задать таблицей истинности.
Особую роль в алгебре логики играют логические функции одной и двух переменных – унарные и бинарные логические операции.
Множество всех логических функций одной переменной P 2 (1) – унарных логических операций – представлено в таблице 1.3.1 своими
|
|
таблицами истинности, | 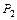 (n)|=4:
(n)|=4:
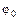 и
и 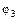 – константы 0 и 1 соответственно.
– константы 0 и 1 соответственно.
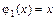 ,
, 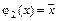 .
.
Таблица 1.3.1

|
Таблица 1.3.2 | |||||||
| № | x 1 | 0 | 0 | 1 | 1 | Обозначения функции | Названия функции |
| x 2 | 0 | 1 | 0 | 1 | |||
| 0 | 0 | 0 | 0 | 0 | j0(x 1, x 2)=const 0 | Константа 0 | |
| 1 | 0 | 0 | 0 | 1 | j1(x 1, x 2)= x 1& x 2, x 1Ù x 2 | Конъюнкция, функция “и” | |
  2 2
| 0 | 0 | 1 | 0 | j2(x 1, x 2)= x 1® x 2, x 1® x 2 | Запрет x 2, левая коимпликация | |
| 3 | 0 | 0 | 1 | 1 | j3(x 1, x 2)= x 1 | Повтор x 1 | |
  4 4
| 0 | 1 | 0 | 0 | j4(x 1, x 2)= x 1 x 2, x 1 x 2 | Запрет x 1, правая коимпликация | |
| 5 | 0 | 1 | 0 | 1 | j5(x 1, x 2)= x 2 | Повтор x 2 | |
| 6 | 0 | 1 | 1 | 0 | j6(x 1, x 2)= x 1Å x 2, x 1∆ x 2 | Сумма по mod 2, неравнозначность | |
| 7 | 0 | 1 | 1 | 1 | j7(x 1, x 2)= x 1Ú x 2 | Дизъюнкция | |
| 8 | 1 | 0 | 0 | 0 | j8(x 1, x 2)= x 1○ x 2, x 1¯ x 2 | Функция Вебба, стрелка Пирса | |
| 9 | 1 | 0 | 0 | 1 | j9(x 1, x 2)= x 1~ x 2, x 1Û x 2 | Эквивалентность, равнозначность | |
 10 10
| 1 | 0 | 1 | 0 | j10(x 1, x 2)= x 2, Ø x 2 | Отрицание x 2 | |
| 11 | 1 | 0 | 1 | 1 | j11(x 1, x 2)= x 1 x 2, x 1Ì x 2 | Обратная (правая) импликация | |
 12 12
| 1 | 1 | 0 | 0 | j12(x 1, x 2)= x 1, Ø x 1 | Отрицание x 1 | |
| 13 | 1 | 1 | 0 | 1 | j13(x 1, x 2)= x 1® x 2, x 1É x 2 | Прямая (левая) импликация | |
| 14 | 1 | 1 | 1 | 0 | j14(x 1, x 2)= x 1| x 2, x 1/ x 2 | Функция (штрих) Шеффера | |
| 15 | 1 | 1 | 1 | 1 | j15(x 1, x 2)=const 1 | Константа 1 | |
Логические функции трех и более переменных обычно задаются также формулами, состоящими из символов, переменных и знаков унарных и бинарных операций.
Формулы 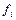 (
( ,...,
,...,  ) и
) и 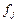 (
( ,...,
,...,  ) называются эквивалентными (равнозначными), если совпадают их таблицы истинности, т.е.
) называются эквивалентными (равнозначными), если совпадают их таблицы истинности, т.е. 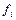 (
( ,...,
,...,  ) =
) = 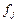 (
( ,...,
,...,  ).
).
Стандартный метод установления эквивалентности двух формул:
1) для каждой формулы составляется таблица истинности;
2) полученные таблицы сравнивают по каждому набору значений переменных;
3) формулы эквивалентны (=), если на сравниваемых наборах значения функции совпадают.
Пример 1. Логическая функция трех переменных задана формулой в префиксной форме:
f ( ,
,  ,
,  ) =
) = 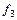 (
(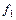 (
( ,
,  ),
), 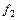 (
( ,
, 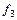 (
( ,
,  )))
)))
Представить f в инфиксной форме, если 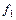 ,
, 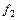 ,
, 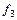 – бинарные операции:
– бинарные операции: 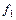 – &,
– &, 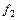 – Å,
– Å, 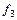 – Ú.
– Ú.
Инфиксная форма заданной логической функции:
f ( ,
,  ,
,  )=(
)=( &
&  )Ú (
)Ú ( Å(
Å(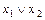 )))
)))
Пример 2. Доказать эквивалентность формулы:
 ¯
¯ 

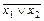

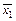 &
& 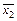
Для доказательства эквивалентности составим таблицу истинности для указанной формулы.
|
Таблица 1.3.3 | |||||||
  x 1 x 1
| x 2 | x 1 |x 2* | x 1& x 2 | x 1& x 2* | x 1 | x 2 | x 1Ú x 2* |
| 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
Формулы  |
|  ,
, 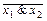 и
и 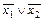 принимают одинаковые значения на одних и тех же наборах значений переменных, следовательно, они представляют одну и ту же функцию:
принимают одинаковые значения на одних и тех же наборах значений переменных, следовательно, они представляют одну и ту же функцию:  |
| 

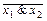

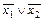 .
.
Пример 3. Проверить истинность правил 1 и 2 схем логически правильных рассуждений (см. 1, 2) построением таблиц истинности.
Правила 1 (Modus Ponens) и 2 (Modus Tollens) представляются логическими формулами:
1. ((A ® B)& A)® B; 2. ((A ® B)&Ø B)®Ø A.
Построенные таблицы истинности этих правил подтверждают их тождественную истинность.
|
Таблица 1.3.4 | |||||||
| A | B | (A ® B)& A | Правило 1: ((A ® B)& A)® B | Ø A | Ø B | (A ® B)&Ø B | Правило 2: ((A ® B)&Ø B)®Ø A |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 |
Вопросы для самопроверки и упражнения.
|
|
1. Представить префиксные формулы логических функций трех переменных f ( ,
,  ,
,  ) в инфиксной форме, если
) в инфиксной форме, если 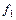 – Ú,
– Ú, 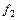 – &,
– &, 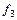 – Å,
– Å, 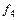 – Ø, и построить соответствующие таблицы истинности:
– Ø, и построить соответствующие таблицы истинности:
1) 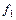 (
( ,
, 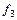 (
( ,
, 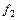 (
(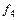 (
( ),
),  )));
)));
2) 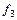 (
(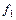 (
( ,
,  ),
), 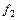 (
( ,
, 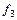 (
( ,
, 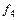 (
( ))));
))));
3) 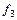 (
(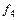 (
( ),
), 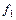 (
( ,
, 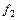 (
( ,
, 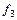 (
( ,
, 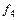 (
( ))))).
))))).
2. Вычислить значения функций f ( ,
,  ,
,  ) на наборах:
) на наборах:
а) (0,1,0); б) (1,1,0);
1) ( ~
~  )®((
)®(( &
&  )Ú
)Ú  );
);
2) ((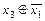 )&
)&  )®(
)®(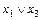 );
);
3) (( ®
®  )&
)&  )~((
)~((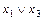 )
) 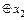 ).
).
3. Доказать справедливость следующих соотношений:
а) x Ú (y Ú z)  (x Ú y) Ú z; г) x ×(y Ú z)
(x Ú y) Ú z; г) x ×(y Ú z)  x × y Ú x × z;
x × y Ú x × z;
б) x ×(y × z)  (x × y)× z; д) x Ú (y × z)
(x × y)× z; д) x Ú (y × z)  (x Ú y)×(x Ú z).
(x Ú y)×(x Ú z).
в) x ×(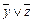 )Ú y × z
)Ú y × z  x Ú y × z;
x Ú y × z;
4. Построением таблиц истинности подтвердить справедливость правил 4–8, 10–11 (см §1.2) логически правильных рассуждений.
Булева алгебра.
Алгебра < 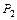 ;å={&,Ú,Ø}>, где
;å={&,Ú,Ø}>, где 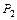 – множество всех логических функций, называется булевой алгеброй. Операции и формулы булевой алгебры называют булевыми.
– множество всех логических функций, называется булевой алгеброй. Операции и формулы булевой алгебры называют булевыми.
Сигнатура å={&,Ú,Ø} функционально полна, т.е. позволяет выразить любые другие логические функции с помощью булевых функций &,Ú,Ø.
Таблица 1.4.1
 x
x
|
Таблица 1.4.2 | |||||
| x 1 | x 2 | x 1Ú x 2 | x 1× x 2 | x 1× x 2Å x 1 | x 1× x 2Å x 1Å x 2 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 | 1 |
Вопросы для самопроверки и упражнения.
1. Функциональной полнотой обладают “усеченные” наборы булевых операций {&,Ú,Ø}: а) {&,Ø}; б){Ú,Ø}.
Для подтверждения их функциональной полноты достаточно выразить базис {&,Ú,Ø} через функции {&,Ø}, {ÚØ}. Проверить справедливость относительно “недостающих” операций:

 а)
а) 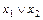 =
= 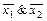 ; б)
; б)  &
&  =
= 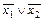 .
.
2. Показать (используя результаты упражнения 1):
1) базис {&,Ø} представим через базис Шеффера {|}:
а) 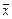 = x | x, б)
= x | x, б)  &
&  =(
=( |
|  ) | (
) | ( |
|  ).
).
2) базис {Ú,Ø} представим через базис Пирса {¯}:
а) 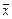 = x ¯ x, б)
= x ¯ x, б) 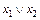 =(
=( ¯
¯  )¯ (
)¯ ( ¯
¯  ).
).
3. Показать, что ниже перечисленные функционально полные системы являются базисами:



 1. {®,~}, 2. {®,○}, 3. {®,®}, 4. {®,Å}, 5. {®,Ø}, 6. {®,Ø}, 7. {®,1}, 8. {~,&,○}, 9. {~,Ú,○}, 10. {Å,&,~}, 11. {Å,Ú,~}, 12. {Å,Ú,1}.
1. {®,~}, 2. {®,○}, 3. {®,®}, 4. {®,Å}, 5. {®,Ø}, 6. {®,Ø}, 7. {®,1}, 8. {~,&,○}, 9. {~,Ú,○}, 10. {Å,&,~}, 11. {Å,Ú,~}, 12. {Å,Ú,1}.
1.5. Эквивалентные преобразования.
1. Правило подстановки формулы F вместо переменной x.
2. Правило замены подформул. Если какая–либо формула F, описывающая функцию f, содержит 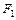 в качестве подформулы, то замена
в качестве подформулы, то замена 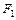 на эквивалентную
на эквивалентную 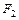 (
(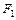 =
= 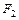 ) не изменит функции f; полученная при такой замене новая формула F ¢ эквивалентна исходной F.
) не изменит функции f; полученная при такой замене новая формула F ¢ эквивалентна исходной F.
Эквивалентные преобразования – преобразования, использующие эквивалентные соотношения и правило замены.
Основные эквивалентные соотношения (законы) в булевой алгебре:
1. Ассоциативность:
а)  ×(
×( ×
×  )
)  (
( ×
×  )×
)× 

 ×
×  ×
×  ;
;
б) 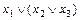

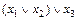

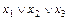 .
.
2. Коммутативность:
а)  ×
× 

 ×
×  ; б)
; б) 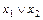

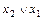 .
.
3. Дистрибутивность:
а)  ×(
×(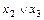 )
) 
 ×
× 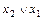 ×
×  ; б)
; б)  Ú(
Ú( ×
×  )=(
)=(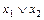 )×(
)×(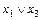 ).
).
4. Идемпотентность: а) x × x  x; б) x Ú x
x; б) x Ú x  x.
x.
5. Закон двойного отрицания: 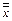
 x.
x.
6. Свойства констант 0 и 1:
а) x ×1  x; б) x Ú 1
x; б) x Ú 1 
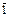 ; в)
; в) 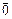
 1;
1;
г) x ×0  0; д) x Ú 0
0; д) x Ú 0 
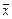 ; е)
; е) 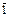
 0.
0.
7. Законы де Моргана:

 а)
а) 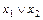

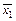 ×
× 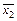 ; б)
; б)  ×
× 

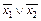 .
.
8. Закон противоречия: x × 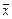
 0.
0.
9. Закон исключенного третьего: 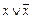
 1.
1.
Другие соотношения, часто применяемые в преобразованиях булевых формул, выводимы с помощью основных законов. Рассмотрим некоторые задачи эквивалентных преобразований в булевой алгебре и способы их решения.
1. Упрощение формул. Для упрощения формул используются следующие эквивалентные соотношения, выводимые из основных с помощью эквивалентных преобразований:
а) x Ú x × y  x, б) x ×(x Ú y)
x, б) x ×(x Ú y)  x – поглощение; (10)
x – поглощение; (10)
x × y Ú x × 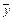
 x – склеивание; (11)
x – склеивание; (11)
x ×z Ú y × 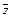 Ú x × y
Ú x × y  x ×z Ú y ×
x ×z Ú y × 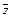 – обобщенное склеивание; (12)
– обобщенное склеивание; (12)
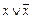 × y
× y  x Ú y. (13)
x Ú y. (13)
Булевой функции к СДНФ.
1. В таблице выбрать все конституенты единицы, т.е. те наборы 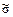 =<
=< 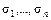 > значений переменных
> значений переменных  ,...,
,...,  , на которых
, на которых 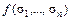 =1.
=1.
2. Каждому набору 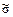 поставить в соответствие элементарную конъюнкцию
поставить в соответствие элементарную конъюнкцию 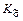 =
= 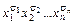 .
.
3. Все полученные элементарные конъюнкции логически сложить, т.е. искомая СДНФ для заданной функции будет:
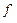 (
( ,...,
,...,  )СДНФ=
)СДНФ= 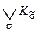
С использованием принципа двойственности для булевых алгебр определяется конъюнктивная нормальная форма (КНФ) и совершенная конъюнктивная нормальная форма (СКНФ).
Булевой функции к СКНФ.
1. В таблице выбрать все конституенты нуля, т.е. те наборы 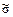 =<
=< 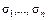 > значений переменных
> значений переменных  ,...,
,...,  , на которых
, на которых 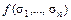 =0.
=0.
2. Каждому набору 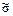 поставить в соответствие элементарную дизъюнкцию
поставить в соответствие элементарную дизъюнкцию 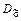 =
= 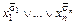 .
.
3. Все полученные элементарные дизъюнкции логически умножить, т.е. искомая СКНФ для заданной функции будет:
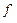 (
( ,...,
,...,  )СКНФ=
)СКНФ= 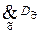 .
.
Пример 1. Построить СДНФ и СКНФ булевой функции, заданной таблицей 1.5.1.
Таблица 1.5.1



