
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
З робочої навчальної програми з предметуСтр 1 из 9Следующая ⇒
ВИТЯГ З робочої навчальної програми з предмету Математика
П/п |
Назва розділів, тем, програми Зміст заняття |
Всього годин |
З них в годинах |
Форма контролю | |||||
| лекції | семінари | Практ. занят. | ||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||||
| ІІ СЕМЕСТР | ||||||||||
| 4. Рівняння, нерівності, системи | 18 | 18 | ||||||||
| 1 | Основні види рівнянь з однією змінною. Загальні методи їх розв’язання: розкладання на множники, заміна невідомої. | 2 | 2 | Бесіда, розв’язання рівнянь. | ||||||
| 2 | Загальні методи розв’язання рівнянь: розкладання на множники, заміна невідомої, функціональні методи. Самостійна робота №1. | 2 | 2 | Бесіда, усне опитування, розв’язання рівнянь. | ||||||
| 3 | Розв’язування задач, які зводяться до рівнянь. | 2 | 2 | Розв’язування задач. | ||||||
| 4 | Розв’язування рівнянь та задач. Самостійна робота №2. | 2 | 2 | Тести, розв’язання рівнянь, задач. | ||||||
| 5 | Нерівності з однією змінною, їх види, методи розв’язання. | 2 | 2 | Бесіда, розв’язання нерівностей. | ||||||
| 6 | Нерівності з однією змінною, їх види, методи розв’язання. Самостійна робота №3 | 2 | 2 | Розв’язання нерівностей. | ||||||
| 7 | Системи нелінійних рівнянь, їх види, методи їх розв’язання. | 2 | 2 | Бесіда, розв’язання систем рівнянь. | ||||||
| 8 | Розв’язування систем нелінійних рівнянь | 2 | 2 | Розв’язування систем нелінійних рівнянь | ||||||
| 9 | Розв’язування рівнянь, нерівностей та систем нелінійних рівнянь Перевірочна робота. Залік з теми. | 2 | 2 | Тестовий контроль, перевірочна робота | ||||||
Тема: ОСНОВНІ ВИДИ РІВНЯНЬ З ОДНІЄЮ ЗМІННОЮ. ЗАГАЛЬНІ МЕТОДИ ЇХ РОЗВ’ЯЗУВАННЯ: РОЗКЛАДАННЯ НА МНОЖНИКИ, ЗАМІНА НЕВІДОМОЇ, ФУНКЦІОНАЛЬНИЙ МЕТОД.
Означення рівняння. Корені рівняння. Поняття рівносильності. Властивості рівняння:
Рівність із змінною, відносно якої треба встановити, для яких її значень (можливо таких значень і не існує) рівність перетворюється у правильну числову називається рівнянням.
Наприклад: 5х - х=28, 2(х+3)=5х -7, х2 - 4=0.
Якщо в рівності одна змінна, то це рівняння з однією змінною.
Коренем (розв’язком) рівняння з однією змінною називається значення змінної, при якому рівняння перетворюється у правильну числову рівність, або при якому змінна задовольняє рівняння.
|
|
Розв’язати рівняння – означає знайти всі його корені (розв’язки) або довести, що рівняння коренів немає.
Якщо рівняння має один корінь, наприклад х=5, то відповідь записують у формі: х = 5 або 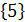 .
.
Якщо рівняння має декілька (скінченне число) коренів, то відповідь зручно записувати у вигляді перерахунку коренів, даючи кожному значенню х свій номер. Наприклад, х1 = - 2 і х2 = 2 або 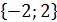 . Корені бажано розташовувати в порядку зростання.
. Корені бажано розташовувати в порядку зростання.
Якщо рівняння зовсім немає коренів, то відповідь записується словами: коренів немає або 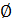 .
.
Два рівняння з однією змінною називаються рівносильними, якщо корені першого рівняння є коренями другого і, навпаки корені другого рівняння є коренями першого.
Властивості рівняння:
1) якщо до обох частин рівняння додати одне й теж саме число чи вираз зі змінною, що не втрачає смислу ні за яких значень змінної, то дістанемо рівняння, рівносильне даному;
звідси випливає, що можна переносити будь-який член рівняння з однієї його частини в іншу, змінюючи попередньо знак цього члена на протилежний;
2) якщо обидві частини рівняння помножити або розділити на одне й теж саме число, що не дорівнює нулю, чи вираз зі змінною, який не перетворюється на нуль ні за яких значень змінної і не втрачає смислу на множині допустимих значень змінної для даного рівняння, то дістанемо рівняння, рівносильне даному.
Лінійні рівняння
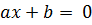
Якщо а 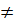 0, то х=
0, то х= 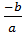 - єдиний корінь;
- єдиний корінь;
Якщо а=0,b=0, то коренем рівняння буде будь-яке дійсне число;
Якщо а=0, 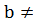 0, то рівняння не має коренів.
0, то рівняння не має коренів.
Квадратні рівняння
2.1. Повне квадратне рівняння:
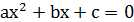 ;
;
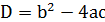 ;
;
якщо 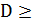 0, то два дійсні корені
0, то два дійсні корені 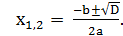
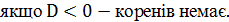
2.2. Неповне зведене квадратне рівняння:
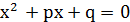
За теоремою Вієта:
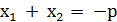 ;
;
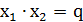 .
.
2.3. Неповне квадратне рівняння:
· 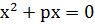 ;
;
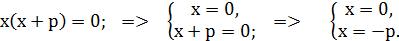
· 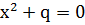 ;
;
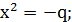
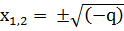 ;
; 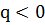 .
.
Просте степеневе рівняння
Просте степеневе рівняння 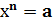 при різних n і а (n- натуральне число):
при різних n і а (n- натуральне число):
1) при будь-якому додатному а рівняння 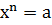 має:
має:
а) при будь-якому непарному n (n=2k-1, kєN) тільки один дійсний корінь х= 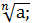
б) при будь-якому парному n (n=2k, kєN) тільки два дійсних корені х=  х=-
х=- 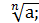
2) при а= 0 рівняння 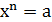 має тільки один корінь х=0;
має тільки один корінь х=0;
|
|
3) при будь-якому від’ємному а рівняння 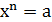 має:
має:
а) при будь-якому непарному n (n=2k-1, kєN) тільки один дійсний корінь х= 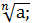
б) при будь-якому парному n (n=2k, kєN) не має дійсних коренів.
Показникове рівняння.
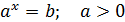
Методи розв’язування простих показникових рівнянь.
1. Порівняння основ: 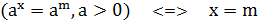 ; Якщо основи рівні, то і показники рівні.
; Якщо основи рівні, то і показники рівні.
2.Порівняння показників:(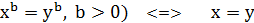 ; Якщо показники рівні, то і основи рівні.
; Якщо показники рівні, то і основи рівні.
3.За означенням степенів: 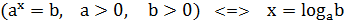 .
.
Логорифмічне рівняння:
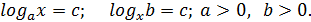
Якщо 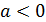 , рівняння не має розв’язку.
, рівняння не має розв’язку.
Методи розв’язання простих логарифмічних рівнянь.
1) За означенням: 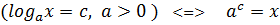 ;
;
2) За порівнянням:  .
.
Тригонометричні рівняння:
v  ;
; 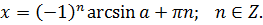
Окремі випадки:
ü 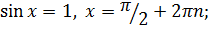
ü 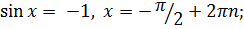
ü 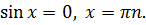
v 

Окремі випадки:
ü 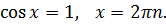
ü 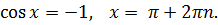
ü 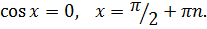
v 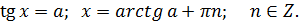
v 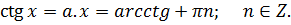
САМОСТІЙНА РОБОТА №1
Варіант -1
Розв’язати рівняння
6б 1. х2 – 2х- 8=0;
2. х3 +16х=0;
9б 3. 33х−9∙32х−3х+9=0;
4. 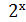 =2+х;
=2+х;
10-11б
5. х3+3х2 +5х+3=0.
6.6sin2 x − 3sin x cos x − 5cos2 x = 2.
Варіант-2
Розв’язати рівняння
6б 1. х2 – 6х + 8=0;
2. х4 - 16х2 =0;
9б 3. 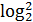 x+
x+ 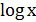 -2=0;
-2=0;
4. 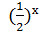 =3 - х;
=3 - х;
10-11б
5. х3+3х2 +5х+3=0.
6. 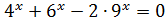
Тема. РОЗВ’ЯЗУВАННЯ ЗАДАЧ, ЯКІ ЗВОДЯТЬСЯ ДО РІВНЯНЬ
Основні види нерівностей
Нерівності з однією змінною поділяються на: алгебраїчні та трансцендетні.
Алгебраїчні - це нерівності утворені з чисел і змінних за допомогою дій додавання, віднімання, множення, ділення, піднесення до цілого додатного степеня і добування арифметичного кореня.
Алгебраїчні поділяють на раціональні (лінійні – 4х+8 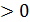 , квадратні – 2х2 +3х - 6
, квадратні – 2х2 +3х - 6 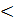 0, біквадратні) та ірраціональні (
0, біквадратні) та ірраціональні (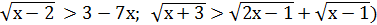 . Раціональні можуть бути як цілими (2х2 +3х - 6
. Раціональні можуть бути як цілими (2х2 +3х - 6 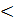 0) так і дробовими (
0) так і дробовими (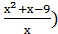
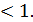
Всі неалгебраїчні нерівності називаютьсятрансцендентними. До них відносяться: показникові, логарифмічні, тригонометричні. Тому основними (стандартними) видами нерівностей є:
Ø Лінійні ах+b 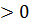 ,
,
Ø Квадратні ax 2 + bx + c 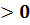 ,
,
Ø Степеневі 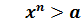 ,
,
Ø Показникові 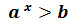 ,
,
Ø Логарифмічні 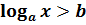 ,
,
Ø тригонометричні sinx 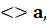 cosx
cosx 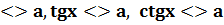
Лінійні нерівності
Лінійною нерівністю з однією змінною називається нерівність виду
ax + b 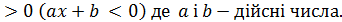
Якщо a 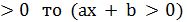
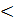 =
= 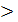 (x
(x 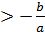 )
) 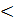 =
= 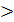 х
х 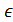 (
(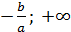 ).
).
Якщо a 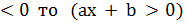
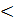 =
= 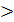 (x
(x 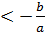 ).
). 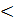 =
= 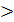 х
х 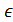 (
(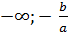 ).
).
Приклад 2. Розв’язати нерівність 2х+3 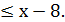
Розв’язування. 2х+3 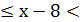 =
= 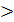 2х- х
2х- х 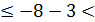 =
= 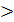 х
х 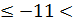 =
= 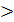
х є (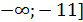 .
.
Відповідь: х є (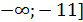 .
.
Приклад 3. Розв’язати нерівність 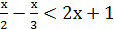
Розв’язування. 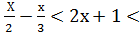 =
= 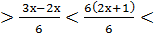 =
= 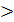
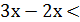 12х+6
12х+6 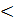 =
= 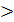 х-12х
х-12х 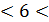 =
= 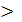 -11х
-11х 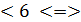 х
х 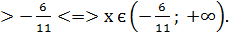
Відповідь: 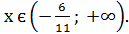
Квадратні нерівності
Нерівності виду ах2+bx+с 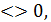 де a, b,с – числа, а
де a, b,с – числа, а 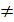 0, х - змінна,
0, х - змінна, 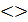 - один із знаків нерівності, називають квадратними.
- один із знаків нерівності, називають квадратними.
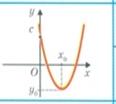
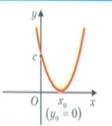
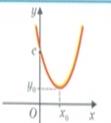
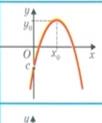
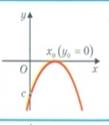
Наприклад 7х2+3х-11 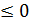 , х2 - 8
, х2 - 8 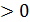 -квадратні нерівності. Розв’язування квадратних нерівностей зводять до відшукання проміжків, на яких відповідна квадратична функція у= ах2+bx+с набуває додатних, від’ємних, невід’ємних, значень. Графіком квадратичної функції є парабола, вітки якої направлені: вгору, якщо а
-квадратні нерівності. Розв’язування квадратних нерівностей зводять до відшукання проміжків, на яких відповідна квадратична функція у= ах2+bx+с набуває додатних, від’ємних, невід’ємних, значень. Графіком квадратичної функції є парабола, вітки якої направлені: вгору, якщо а 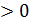 і вниз, якщо а
і вниз, якщо а 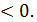 Знайдемо нулі функції ах2+bx+с=0 та проміжки на яких функція. набуває додатних, від’ємних, невід’ємних, недодатних значень
Знайдемо нулі функції ах2+bx+с=0 та проміжки на яких функція. набуває додатних, від’ємних, невід’ємних, недодатних значень
| ах2+bx+с=0 | |||
|
а | 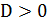
| D=0 | D 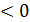
|
| 
| 
| |
а 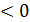
|
| 
| 
|
Показникові нерівності
Нерівність, яка містить змінну величину в показнику степеня, називають показниковою.
Наприклад, 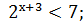
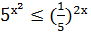 тощо. Розв’язування показникових нерівностей ґрунтується на властивостях показникової функції:
тощо. Розв’язування показникових нерівностей ґрунтується на властивостях показникової функції:
Ø функція у= 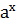 зростає, якщо а
зростає, якщо а 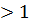 ,
,
Ø функція у= 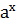 спадає, якщо
спадає, якщо 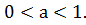
Ø функція у= 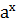 набуває лише додатних значень.
набуває лише додатних значень.
|
|
Тобто, якщо а 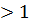 , то
, то 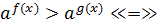 f (x)
f (x) 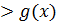
якщо 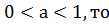
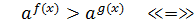 f (x)
f (x) 
Логарифмічні нерівності
Нерівність, яка містить змінну величину під знаком логарифма або в його основі, називають логарифмічною. Наприклад, 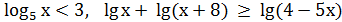 тощо. Розв’язування логарифмічних нерівностей ґрунтується на властивості монотонності логарифмічної функції: функція у=
тощо. Розв’язування логарифмічних нерівностей ґрунтується на властивості монотонності логарифмічної функції: функція у= 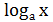 монотонно зростає, якщо а
монотонно зростає, якщо а 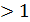 , і монотонно спадає, якщо
, і монотонно спадає, якщо 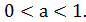 При цьому слід ураховувати, що підлогарифмічний вираз може набувати лише додатних значень. Тобто
При цьому слід ураховувати, що підлогарифмічний вираз може набувати лише додатних значень. Тобто 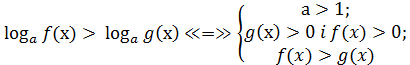 =
= 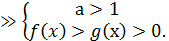
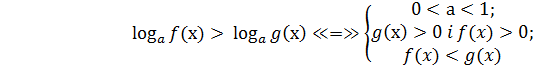 =
= 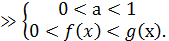
Тригонометричні нерівності
Нерівності, які містить змінну величину під знаком тригонометричної функції, називають тригонометричними. Наприклад, cos x 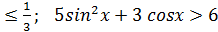 тощо. Розв’язування тригонометричних нерівностей зводять до розв’язування найпростіших тригонометричних нерівностей. Найпростіші тригонометричні нерівності – це нерівності виду sinx
тощо. Розв’язування тригонометричних нерівностей зводять до розв’язування найпростіших тригонометричних нерівностей. Найпростіші тригонометричні нерівності – це нерівності виду sinx 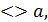 cosx
cosx 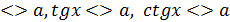 . Розв’язуватинайпростіші тригонометричні нерівності можна графічно або за допомогою одиничного кола.
. Розв’язуватинайпростіші тригонометричні нерівності можна графічно або за допомогою одиничного кола.
За означенням, синусом кута 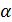 є ордината точки
є ордината точки 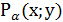 одиничного кола, а косинусом - абсциса точки
одиничного кола, а косинусом - абсциса точки 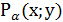 одиничного кола. Цей факт використовується при розв’язуванні тригонометричних нерівностей виду sinx
одиничного кола. Цей факт використовується при розв’язуванні тригонометричних нерівностей виду sinx 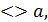 cosx
cosx 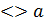 за допомогою одиничного кола.
за допомогою одиничного кола.
Розв’язування нерівностей з однією змінною передбачає два кроки:
Ø перетворення нерівностей до стандартної (до одного з основних видів нерівностей з однією змінною);
Ø розв’язування стандартної нерівності.
Перетворення нерівності до стандартної (до одного з основних видів нерівностей з однією змінною) здійснюються за відомими формулами, які завжди можна відновити в пам’яті при допомозі довідників або ж просто їх пам’ятати.
Нерівності з модулем.
Модуль дійсного числа (позначається 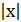 )дорівнює самому числу х, якщо х додатнє, дорівнює (-х), якщо х від’ємне, і модуль нуля дорівнює нулю.
)дорівнює самому числу х, якщо х додатнє, дорівнює (-х), якщо х від’ємне, і модуль нуля дорівнює нулю.
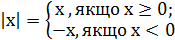
При розв’язуванні нерівностей, які містять змінну під знаком модуля, використовують наступні рівносильні перетворення:
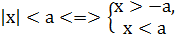
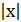
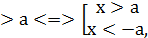
Приклад 4. Розв’язати нерівність 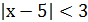
Розв’язування. 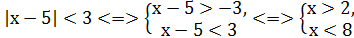
Відповідь: х є (2;8)
Приклад 5. Розв’язати нерівність 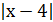
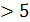
Розв’язування 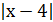
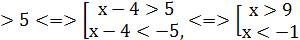
Відповідь: х є (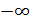 ; -1)
; -1) 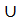 (9; +
(9; + 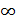 ).
).
Розв’язуючи нерівність виду 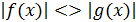 , застосовують піднесення обох частин нерівності до квадрата.
, застосовують піднесення обох частин нерівності до квадрата.
Приклад 6. Розв’язати нерівність 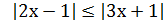 ,
,
Розв’язування. При піднесенні до квадрата обох частин нерівності одержимо:
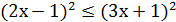 ; 4х2 - 4х +1
; 4х2 - 4х +1 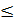 9х2 +6х+1; 5х2 +10х
9х2 +6х+1; 5х2 +10х 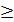 0; х(х+2)
0; х(х+2) 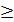 0.
0.
х 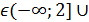 [0;
[0; 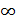 ).
).
Відповідь: 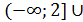 [0;
[0; 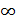 ).
).
Перетворення нерівності до одного з основних видів нерівностей з однією змінною є головним кроком при розв’язуванні нерівностей. Повністю алгоритмізувати процес перетворення неможливо, але дуже важливо запам’ятати прийоми, які найбільше використовуються та загальні для всіх типів нерівностей.
|
|
3) Розкладання на множники.
Якщо дану нерівність при допомозі перетворень можна звести до виду
f(x)∙g(x)<>0. То дана нерівність буде рівносильна сукупності двох більш простих систем нерівностей 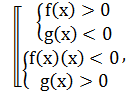 в області визначення нерівності f(x)∙g(x) <>0 або використати метод інтервалів.
в області визначення нерівності f(x)∙g(x) <>0 або використати метод інтервалів.
Приклад 7. Розв’язати нерівність 6 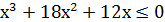 .
.
Розв’язування: 6 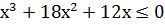 . Винесемо за дужки спільний множник 6х. 6
. Винесемо за дужки спільний множник 6х. 6 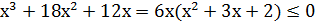 . Знайдемо корені:
. Знайдемо корені:
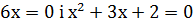 .Звідси маємо х= 0, х = -1, х = -2.Нанесемо на числову пряму отримані числа. Провівши «криву знаків» визначимо знак f(x) в кожному з інтервалів (рис.1). Множина, що дає розв’язки початкової нерівності заштрихована на рис.1.
.Звідси маємо х= 0, х = -1, х = -2.Нанесемо на числову пряму отримані числа. Провівши «криву знаків» визначимо знак f(x) в кожному з інтервалів (рис.1). Множина, що дає розв’язки початкової нерівності заштрихована на рис.1.
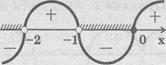
Рис.1
САМОСТІЙНА РОБОТА № 3
В-1
Розв’язати нерівність:
6б. 1.3(х - 2) 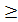 4х – 9; 4х – 9;
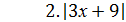 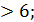 9б. 3.(6 - х)(х+3)(х- 4
9б. 3.(6 - х)(х+3)(х- 4 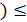 0; 0;
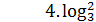 x – x – 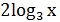 - 3 - 3 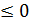 ;
10б. 5 ;
10б. 5 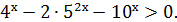
| В-2
Розв’язати нерівність:
6б. 1. 2(х + 3) 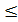 4х +10;
2. 4х +10;
2. 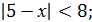 9б. 3. (4-х)(х+2)(х-3)
9б. 3. (4-х)(х+2)(х-3) 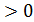 4.
4. 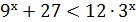 ;
10б. 5. ;
10б. 5. 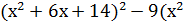 +6х+15)+9 +6х+15)+9 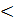 0 0
|
Тема. ОСНОВНІ ВИДИ СИСТЕМ НЕЛІНІЙНИХ РІВНЯНЬ ТА МЕТОДИ ЇХ РОЗВ’ЯЗУВАННЯ.
Кілька рівнянь з двома (або більше) змінними утворюють систему рівнянь, якщо ставиться задача знайти множину спільних розв’язків цих рівнянь. Систему двох рівнянь з двома змінними позначають фігурними дужками і, зазвичай, записують у вигляді
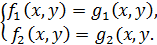 Наприклад
Наприклад 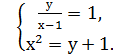
Розв’язати систему рівнянь – значить знайти всі її розв’язки або довести, що розв’язків немає. Система називається сумісною, якщо вона має хоча б один розв’язок, і несумісною,якщо вона не має жодного розв’язку.
Система рівнянь називається визначеною, якщо вона має скінченне число розв’язків, і невизначеною, якщо вона має нескінченну множину розв’язків.
Дві системи називаються рівносильними, якщо вони мають одну і ту саму множину розв’язків (тобто кожний розв’язок першої системи на цій множині є розв’язком другої, і навпаки кожний розв’язок другої системи є розв’язком першої).
Областю допустимих значень (ОДЗ) системи називають спільну область визначення всіх функцій, що входять до запису цієї системи.
Усі рівносильні перетворення систем виконуються на ОДЗ початкової системи.
Найпростіші властивості рівносильних систем:
1. Якщо змінити порядок запису рівнянь заданої системи, одержимо систему, рівносильну заданій.
2. Якщо одне з рівнянь системи замінити на рівносильне йому рівняння, то одержимо систему, рівносильну заданій.
3. Якщо в системі рівнянь з одного рівняння виразити одну змінну через інші й одержаний вираз підставити замість цієї змінної в усі інші рівняння системи, то одержимо систему, рівносильну заданій (на її ОДЗ).
4. Якщо будь-яке рівняння системи замінити сумою цього рівняння, помноженого на число 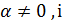 якогось іншого рівняння системи помноженого на число
якогось іншого рівняння системи помноженого на число 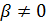 (а усі рівняння залишити без зміни), то одержимо систему, рівносильну заданій.
(а усі рівняння залишити без зміни), то одержимо систему, рівносильну заданій.
|
|
Системи- наслідки. Якщо кожний розв’язок першої системи рівнянь є розв’язком другої, то другу систему називають наслідком першої. При використанні систем-наслідків можлива поява сторонніх коренів, тому перевірка підстановкою розв’язку в початкову систему є складовою розв’язування системи.
Приклад 1. Розв’яжіть систему 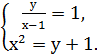
Розв’язування. Із першого рівняння системи у = х-1.Підставимо в друге рівняння системи й одержимо 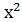 = х. Звідси маємо
= х. Звідси маємо 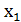 = 0,
= 0, 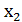 =1. Тоді
=1. Тоді 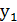 = -1,
= -1, 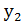 = 0.
= 0.
Перевірка. Пара чисел (0;-1) задовольняє обидва рівняння системи і є її розв’язком. Пара чисел (1;0) не задовольняє перше рівняння системи і не є розв’язком системи.
Відповідь: (0;-1).
Основні методи розв'язування систем рівнянь:
1) Метод підстановки. Спочатку за допомогою якого-небудь рівняння системи виражають одну змінну через іншу. Отриманий вираз підставляють в інше рівняння системи, в результаті чого приходять до рівняння з одною змінною, потім розв’язують це рівняння і знаходять відповідне значення іншої змінної.
Приклад 2. Розв’яжіть систему 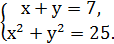
Розв’язування. Із першого рівняння системи у виразимо через х, тобто
у = 7- х. Підставивши в друге рівняння системи замість у вираз (7- х), дістаємо
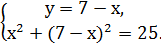
З другого рівняння системи знаходимо х.
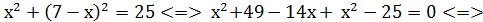
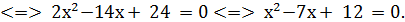 Звідси маємо
Звідси маємо 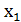 = 3,
= 3, 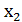 =4. Тоді
=4. Тоді 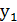 = 4,
= 4, 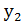 = 3.
= 3.
Таким чином маємо (3;4); (4;3)
Відповідь: (3;4); (4;3).
2) Метод алгебраїчного додавання. При розв’язуванні системи цим методом переходять від даної системи до рівносильної їй системи, в якій одне з рівнянь містить лише одну змінну. При цьому звичайно множать одне або обидва рівняння на числові множники таким чином, щоб коефіцієнти при х або у були однаковими, але з протилежними знаками.
Приклад 3. Розв’яжіть систему 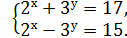
Розв’язування. Розв’яжемо систему рівнянь способом додавання. До першого рівняння додамо друге і отримаємо:

Знаходимо х з першого рівняння. 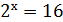
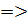 х=4. Підставивши х=4 в друге рівняння отримаємо
х=4. Підставивши х=4 в друге рівняння отримаємо 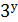 =1. Звідси у=0. Отже х = 4, у = 0
=1. Звідси у=0. Отже х = 4, у = 0
Відповідь: (4;0).
Графічний метод.
Щоб розв’язати систему рівнянь із двома змінними графічним способом, потрібно побудувати графіки рівнянь системи в одній системі координат і знайти координати спільних точок цих графіків: ці координати і є розв’язками системи. Але спочатку виконаємо рівносильні перетворення заданої системи так, щоб було зручно будувати графіки всіх рівнянь, що входять до системи. Потім будуємо відповідні графіки і знаходимо координати точок перетину відповідних кривих: ці координати і є розв’язками системи
Приклад 5. Розв’яжіть систему
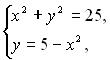
Розв’язування. Обидва рівняння якої є рівняннями другого степеня. Графіком рівняння 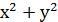 =25 є коло, а графіком рівняння у = 5 -
=25 є коло, а графіком рівняння у = 5 - 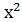 – парабола (рис.1) Ці графіки мають три спільні точки: (0;5), (-3;-4), (3;-4).
– парабола (рис.1) Ці графіки мають три спільні точки: (0;5), (-3;-4), (3;-4).
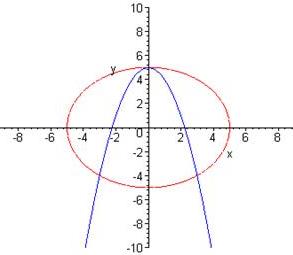
Рис.1
Легко перевірити, що координати кожної з цих точок є розв’язком як першого, так і другого рівнянь системи. Тобто, система має 3 розв’язки.
Відповідь: (0;5), (-3;-4), (3;-4).
Але цей спосіб не є основним способом розв’язування системи рівнянь, тому що він не завжди дає точні результати.
Види систем рівнянь
Симетричною системою рівнянь називається система, всі рівняння якої симетричні.
Вираз f (x,y) називається симетричним, якщо при заміні х на у, у на х він не змінюється.
Приклади симетричних виразів:
f(x,y) = х + у; f(x,y) = 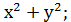 f(x,y) =
f(x,y) = 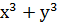
f(x,y) = 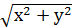 + ху; f(x,y) =
+ ху; f(x,y) = 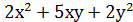 .
.
Вирази (x+y) і xy називаються основними симетричнимимногочленами з двома змінними. Усі симетричні вирази з двома змінними виражаються через основні симетричні многочлени, наприклад:
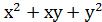 =
= 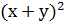 - ху;
- ху; 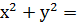
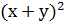 - 2ху;
- 2ху;
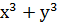 = (х+у)(
= (х+у)(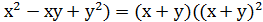 - 3ху) =
- 3ху) = 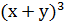 - 3(х + у)ху.
- 3(х + у)ху.
Симетричною системою рівнянь називається система, усі рівняння якої симетричні. Розв’язати симетричну систему можна, наприклад, за допомогою заміни змінних, де новими змінними є основні основні симетричні многочлени.
Приклад 6. Розв’яжіть систему 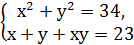
Оскільки 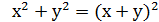 - 2ху, то, поклавши х+у=
- 2ху, то, поклавши х+у= 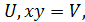 приходимо до такої ситеми:
приходимо до такої ситеми: 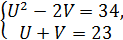 Із цієї системи знаходимо
Із цієї системи знаходимо 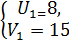 ;
; 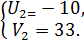 Звідси має сукупність
Звідси має сукупність 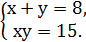 ;
; 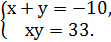
Перша система сукупності має розв’язки (3;5), (5;3); друга система розв’язків не має.
Відповідь:(3;5), (5;3).
Система двох рівнянь з двома змінними називається однорідною, якщо ліві частини її рівнянь, що містять змінні, є однорідними многочленами степеня п від двох змінних. Таким чином, однорідна система з двома змінними має вигляд
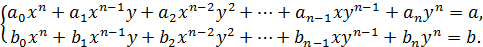
Приклад 7. Розв’яжіть систему 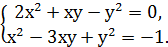
Розв’язування. Ліві частини обох рівнянь системи – однорідні многочлени другого степеня від змінних х і у. Якщо в першому рівнянні покласти=0, то дістанемо 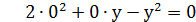
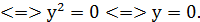
Однак пара (0;0), що є розв’язком першого рівняння системи, не задовольняє другому рівнянню, тому що 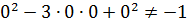 (це не приведе до втрати коренів). Поділивши обидві частини першого рівняння на
(це не приведе до втрати коренів). Поділивши обидві частини першого рівняння на 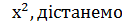
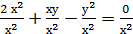
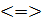 2+
2+ 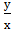 -
- 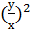 =0
=0 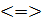
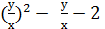 =0. Зробивши заміну
=0. Зробивши заміну 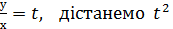 – t - 2= 0
– t - 2= 0 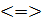
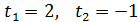 . Тоді
. Тоді 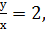 у=2х (х
у=2х (х 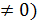 або
або 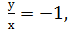 у=-х (х
у=-х (х 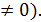
Таким чином, початкова система рівносильна сукупності двох систем рівнянь:
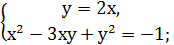
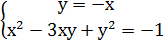
Перша з цих систем має два розв’язки: 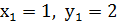 ;
; 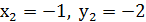
Друга система несумісна. Звідси (1;2), (-1;-2) – розв’язок початкової системи.
Відповідь: (1;2), (-1;-2).
ЗАПИТАННЯ І ЗАВДАННЯ ДЛЯ ПОВТОРЕННЯ.
1.Що таке система двох рівнянь з двома змінними?
2.Що називається розв’язком системи двох рівнянь з двома змінними?
3. Що означає розв’язати систему двох рівнянь з двома змінними?
4. Які дві системи рівнянь називаються рівносильними?
5. Назвати основні способи розв’язування систем рівнянь з двома змінними.
В чому полягає кожний із способів?
ВПРАВИ.
Розв’язати систему рівнянь:
Середній рівень
1) 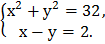 2)
2) 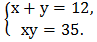 3)
3) 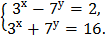 4)
4) 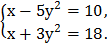
Достатній рівень
5) 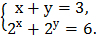 6)
6) 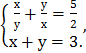 . 7)
. 7) 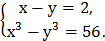 8)
8) 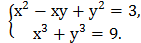
Високий рівень
9) 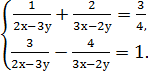 10)
10) 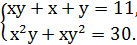 11)
11) 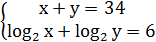
Перевірочна робота
ВАРІАНТ 1
Початковий і середній рівні.
1. Укажіть пару рівносильних рівнянь:
А)2х - 6=4 і х - 2=4; Б) 3х - 6=0 і 2х=4;
В) х2 - 9=0 і х+3=0; Г) х2 - 3х – 4=0 і х+1=0.
2. Яке рівняння не має коренів?
А) 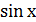 = 2; Б)
= 2; Б) 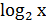 = 1; В) х3 = 2; Г)
= 1; В) х3 = 2; Г) 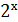 = 1.
= 1.
3. Укажіть систему, яка відповідає умові задачі: «Число х на 3 менше від числа у, а їхній добуток дорівнює 88. Чому дорівнюють ці числа?».
А) 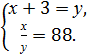 Б)
Б) 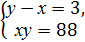 В)
В) 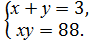 Г)
Г) 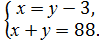
4..Знайдіть множину розв’язків нерівності 3(х - 2) 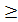 4х – 9.
4х – 9.
5. Розв’яжіть рівняння х4 - 8х = 0.
6. Розв’яжіть нерівність | x −1| 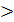 2.
2.
Достатній рівень
7. Розв’яжіть рівняння 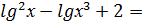 0.
0.
8. Розв’яжіть систему рівнянь 
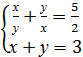
9. Двоє робітників виготовили за перший день 100 деталей. За другий день перший робітник виготовив деталей на 20 % більше, ніж за перший день, а другий робітник - на 10 % більше, ніж за перший день. Усього за другий день вони виготовили 116 деталей. Скільки деталей виготовив за перший день перший робітник?
Високий рівень
У завданні 10 необхідно надати докладні пояснення.
10. Розв’яжіть рівняння 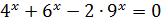
ВАРІАНТ 2
Початковий і середній рівні.
1. Яке рівняння рівносильне рівнянню sin x =2?



