
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Возвращение к исходному интегралу ⇐ ПредыдущаяСтр 4 из 4
Формула интегрирования по частям применима и для нахождения интегралов вида Пример 9. Найти I = D Положим Следовательно, I = Для вычисления интеграла Таким образом, I= Так как в правой части стоит искомый интеграл, то, перенося его в левую часть, получим:
Отсюда получаем окончательный результат:
Применим изложенный метод к вычислению еще двух, часто используемых в приложении, интегралов. Пример 10. Найти I = D Положим
Так как
(см. лекция 2, п.2б, пример 20). Подставив полученное выражение в равенство (*), будем иметь
Таким образом, Пример 11. Найти D Положим
или Отсюда получаем: Понятие о рекуррентных формулах Иногда интегрирование по частям позволяет получить соотношение между неопределенным интегралом, содержащим степень некоторой функции, и аналогичным интегралом, но с меньшим показателем степени той же функции. Подобные соотношения называются рекуррентными формулами. Выведем рекуррентную формулу для интеграла D При n =1 имеем табличный интеграл Пусть n > 1. Представив единицу в числителе как разность Во втором интеграле применим метод интегрирования по частям:
Тогда
Таким образом, интеграл
Проверим нашу готовность приступить к интегрированию основных классов элементарных функций, вычислив интеграл D
Вычислим также интеграл I= Далее полагаем u = eax , dv= cosbxdx, du= aeaxdx, v=
Получаем уравнение относительно неизвестного интеграла I. Решая его, находим
* Дифференциал функции сохраняет одно и то же выражение независимо от того, является ли ее аргумент u независимой переменной или функцией от независимой переменной. Это свойство называется инвариантностью, т.е. неизменностью формы дифференциала.
|
|||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 178; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.202.187 (0.008 с.) |
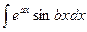 и
и 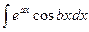 , где а и b – числа. При нахождении этих интегралов она применяется последовательно два раза, причем оба раза за u выбирается либо показательная функция, либо тригонометрическая. После двукратного интегрирования по частям получается линейное уравнение относительно искомого интеграла.
, где а и b – числа. При нахождении этих интегралов она применяется последовательно два раза, причем оба раза за u выбирается либо показательная функция, либо тригонометрическая. После двукратного интегрирования по частям получается линейное уравнение относительно искомого интеграла. .
.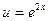 ,
, 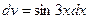 . Тогда
. Тогда 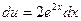 ,
, 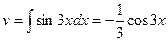 .
. .
.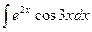 снова применим интегрирование по частям. Положим
снова применим интегрирование по частям. Положим 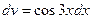 . Тогда
. Тогда 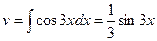 .
.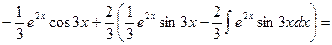
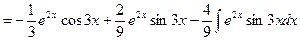 .
. .
.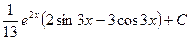 . Ñ
. Ñ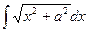 .
. ,
, 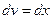 . Тогда
. Тогда 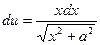 ,
, 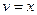 . Следовательно,
. Следовательно,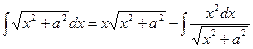
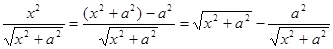 , то
, то
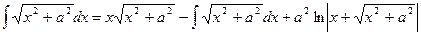 .
.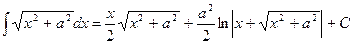 . Ñ
. Ñ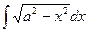 , (а >0)
, (а >0)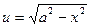 ,
,  ,
, 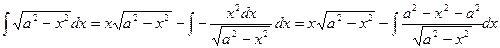 ,
,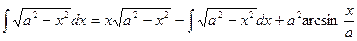 .
.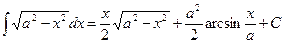 . Ñ
. Ñ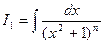 , где n – целое положительное число.
, где n – целое положительное число. .
. , получим
, получим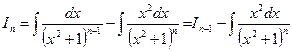 .
.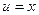 ,
, 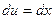 ,
, 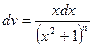 ,
, 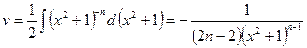 .
.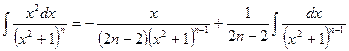 . Следовательно,
. Следовательно,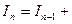
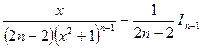 , откуда
, откуда 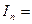
 .
.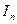 выражен через
выражен через 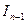 :
: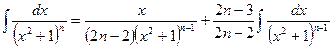 (n >1). Ñ
(n >1). Ñ , последовательно применяя методы непосредственного интегрирования, подведения функции под знак дифференциала и интегрирование по частям.
, последовательно применяя методы непосредственного интегрирования, подведения функции под знак дифференциала и интегрирование по частям.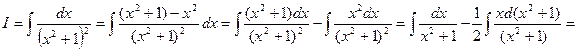
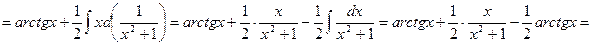
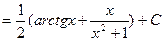 . Ñ
. Ñ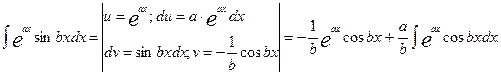
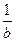 sinbx. Следовательно
sinbx. Следовательно 
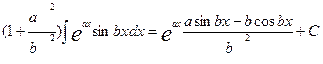 или
или 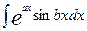 =
=  .
.


