
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Неопределенный интеграл и его свойстваСтр 1 из 4Следующая ⇒
Неопределенный интеграл и его свойства 1. Понятие первообразной функции и неопределенного интеграла Одной из основных задач дифференциального исчисления является отыскание производной заданной функции. Разнообразные вопросы математического анализа и его многочисленные приложения в геометрии, механике, физике и технике приводят к обратной задаче: по данной функции f(x) найти такую функцию F(x), производная которой была бы равна функции f(x), т.е. F'(x) = f(x). Восстановление функции по известной производной этой функции – одна из основных задач интегрального исчисления. Определение 1. Дифференцируемая функция F(x), определенная на некотором промежутке X, называется первообразной (для, от) функции f(x), определенной на том же промежутке, если во всех точках этого промежутка выполняется равенство
или, что то же самое,
Пример 1. Функция F(x) = х 3 является первообразной функции f(x) = 3 х 2 на всей числовой оси, так как при любом x (х 3)' = 3 х 2 .Нетрудно заметить, что первообразная х 3 не является единственной для функции 3 х 2. В самом деле, в качестве первообразной можно было бы взять и функции х 3 + 8, х 3 – 4 и, вообще, х 3+С, где С – произвольная постоянная, потому, что (х 3 +С)' = 3 х 2. Покажем, что множество функций F(x) + С, где F(x) - некоторая первообразная для функции f(x), а С – произвольная постоянная, исчерпывает все первообразные для этой функции. Лемма. Функция, производная которой на некотором промежутке X равна нулю, постоянна на этом промежутке. Доказательство: Пусть во всех точках промежутка X производная функции f(x) равна нулю, т.е f '(x) = 0. Для любых двух точек х 1, х 2 Î X по теореме Лагранжа получаем:
Так как f ' (x) = 0, то f(x2) = f(x1). Это и означает, что значения функции во всех точках промежутка одинаковы, т.е. f(x) = С, где С – некоторое число. Теорема. Если F1(x) и F2(x) - две первообразные для f(x) в некотором промежутке, то разность между ними в этом промежутке равна постоянному числу. Доказательство: Пусть, например, указанный промежуток – интервал ]а;b[. Из определения первообразной имеем: F1'(x) = f(x) и F2'(x) = f(x) для любого х Î ]а;b[. Пусть a (х) = F2(x) - F1(x). Тогда для любого х из ]а;b[ a'(х) = F2'(x) - F1'(x) = f (x) – f (x) = 0. Следовательно, согласно лемме, a (х)
Подчеркнем важный факт: если производная для функции одна, т.е. операция дифференцирования однозначна, то нахождение первообразной для функции возможно лишь с точностью до некоторого постоянного слагаемого. Определение 2. Совокупность всех первообразных для функций f(x), определенных на некотором промежутке X, называется неопределенным интегралом от функции f(x) на этом промежутке и обозначается символом Таким образом, по определению,
если F'(x) = f(x). Значит, чтобы найти неопределенный интеграл от заданной функции, нужно найти какую-нибудь одну ее первообразную и прибавить к ней произвольную постоянную С. Наличие этой постоянной делает задачу нахождения функции по ее производной не вполне определенной. Отсюда происходит само название “неопределенный интеграл”. Определение 3. Нахождение первообразной для данной функции f(x) называется интегрированием функции f(x). Определение 4. Функция f(x) называется подынтегральной функцией, f(x) dх – подынтегральным выражением, х - переменной интегрирования, символ ∫ - знаком неопределенного интеграла, С – постоянной интегрирования. Пример 2. Найти D Так как x 3 =
Слово “интеграл” происходит от латинского “integer”, что означает “восстановленный”. Интегрируя какую-нибудь функцию, в примере 2 функцию x3, мы как бы восстанавливаем функцию
 Тогда геометрически неопределенный интеграл Тогда геометрически неопределенный интеграл
представляет собой семейство интегральных кривых, каждая из которых получается из любой другой кривой параллельным переносом вдоль оси Оу. Отметим без доказательства, что если функция f(x) непрерывна на некотором промежутке X, то на этом промежутке существует первообразная функции f(x), а следовательно, и неопределенный интеграл
Таблица основных интегралов Интегрирование есть действие, обратное дифференцированию. Поэтому, для того чтобы проверить, правильно ли найден данный интеграл, достаточно продифференцировать найденную первообразную. Если при этом получим подынтегральную функцию, то интеграл найден верно. Из определения интеграла следует, что всякая формула для производной конкретной функции, т.е. формула вида (1) может быть записана в виде интегральной формулы (3). Формулы интегрирования получаются обращением соответствующих формул дифференцирования. Используя это соображение и таблицу производных, составим следующую таблицу неопределенных интегралов. 1. В частности, при a = 0 имеем 2. 3. В частности, 3а. 4. 5. 6. 7. 8. 9.
Заметим, что формулы 2,6,7,8 справедливы лишь для тех значений х, при которых не происходит обращения в нуль знаменателя. Для вывода этих формул, как уже отмечалось, используется свойство в) неопределенного интеграла, а именно, дифференцирование правой части равенства. Производная правой части равенства дает подынтегральную функцию, а дифференциал -подынтегральное выражение. Справедливость всех представленных интегралов легко проверить, если продифференцировать их правые части.
Проверим, например, формулу 2. Чтобы найти В промежутке В промежутке
Итак, оба промежутка непрерывности подынтегральной функции объединяются записью
Приведенные интегралы 1-9 принято называть табличными.
Лекция 2. Основные методы интегрирования Пример 3.
Пример 4.
Пример 5.
= = В некоторых случаях нахождение интегралов упрощается применением искусственных приемов. Пример 6. Найти D Умножив подынтегральное выражение на
= Пример 7.
Пример 8.
Пример 11.
Приведем далее примеры вычисления интегралов, которые нам понадобятся в теории интегрирования рациональных дробей. Пример 12. Найти I= D Представим подынтегральную функцию в виде:
Следовательно, I= = Таким образом, Пример 12а. Найти I= D Так как следовательно I = Пример 13. Найти D Для того, чтобы свести этот интеграл к табличному, разделим числитель и знаменатель подынтегрального выражения на
Мы подвели постоянный множитель Вычислим также интеграл, который имеет важное значение при интегрировании иррациональных функций. Пример 14. Найти I= D Имеем Итак, Представленные примеры иллюстрируют важность умения приводить данное дифференциальное выражение В этих примерах были проведены преобразования дифференциала, такие как
часто используемые при нахождении интегралов. В таблице основных интегралов предполагалось, что x есть независимая переменная. Однако, эта таблица, как следует из изложенного выше, полностью сохраняет свое значение, если под x понимать любую непрерывно дифференцируемую функцию от независимой переменной. Обобщим ряд формул таблицы основных интегралов. 3а. 4. 5. 6. 7. 8. 9.
Операция подведения функции Пример 15. Найти I= D Произведем замену переменной по формуле Заменив u его выражением I= Выполненное преобразование эквивалентно подведению под знак дифференциала функции Пример 16. Найти D Положим
Пример 17. Найти D Пусть
В заключение отметим, что разные способы интегрирования одной и той же функции иногда приводят к функциям, различным по своему виду. Это кажущееся противоречие можно устранить, если показать, что разность между полученными функциями есть постоянная величина (см. теорему, доказанную на лекции 1). Примеры: а)
Результаты отличаются на постоянную величину, и, значит, оба ответа верны. б) I=
Легко убедиться, что любые из ответов отличаются друг от друга только на постоянную величину. б) Метод подстановки (метод введения новой переменной) Пусть интеграл
Формула (3) называется формулой замены переменной в неопределенном интеграле. Как правильно выбрать подстановку? Это достигается практикой в интегрировании. Но можно установить ряд общих правил и некоторых приемов для частных случаев интегрирования. Правило интегрирования способом подстановки состоит в следующем. 1. Определяют, к какому табличному интегралу приводится данный интеграл (предварительно преобразовав подынтегральное выражение, если нужно). 2. Определяют, какую часть подынтегральной функции заменить новой переменной, и записывают эту замену.
3. Находят дифференциалы обеих частей записи и выражают дифференциал старой переменной (или выражение, содержащее этот дифференциал) через дифференциал новой переменной. 4. Производят замену под интегралом. 5. Находят полученный интеграл. 6. Производят обратную замену, т.е. переходят к старой переменной.
Проиллюстрируем правило примерами. Пример 18. Найти D Положим
= Пример 19. Найти D Вычислим интеграл
Этот интеграл найдем подведением
Пример 20. Найти D Применим подстановку Эйлера:
Таким образом, имеем Студенты прозвали этот интеграл «длинным логарифмом». Иногда вместо подстановки Пример 21. Найти D Полагая t= ex , получаем
Пример 22. Найти D Воспользуемся подстановкой Следовательно, В ряде случаев нахождение интеграла основывается на использовании методов непосредственного интегрирования и подведения функций под знак дифференциала одновременно (см. пример 12). Проиллюстрируем этот комбинированный подход к вычислению интеграла, играющего важную роль при интегрировании тригонометрических функций. Пример 23. Найти D Имеем = Итак, Другой подход к вычислению этого интеграла:
Пример 24. Найти Заметим, что удачный выбор подстановки обычно представляет трудности. Для их преодоления необходимо овладеть техникой дифференцирования и хорошо знать табличные интегралы. Лекция 3. Неопределенный интеграл и его свойства 1. Понятие первообразной функции и неопределенного интеграла Одной из основных задач дифференциального исчисления является отыскание производной заданной функции. Разнообразные вопросы математического анализа и его многочисленные приложения в геометрии, механике, физике и технике приводят к обратной задаче: по данной функции f(x) найти такую функцию F(x), производная которой была бы равна функции f(x), т.е. F'(x) = f(x). Восстановление функции по известной производной этой функции – одна из основных задач интегрального исчисления. Определение 1. Дифференцируемая функция F(x), определенная на некотором промежутке X, называется первообразной (для, от) функции f(x), определенной на том же промежутке, если во всех точках этого промежутка выполняется равенство
или, что то же самое,
Пример 1. Функция F(x) = х 3 является первообразной функции f(x) = 3 х 2 на всей числовой оси, так как при любом x (х 3)' = 3 х 2 .Нетрудно заметить, что первообразная х 3 не является единственной для функции 3 х 2. В самом деле, в качестве первообразной можно было бы взять и функции х 3 + 8, х 3 – 4 и, вообще, х 3+С, где С – произвольная постоянная, потому, что (х 3 +С)' = 3 х 2.
Покажем, что множество функций F(x) + С, где F(x) - некоторая первообразная для функции f(x), а С – произвольная постоянная, исчерпывает все первообразные для этой функции. Лемма. Функция, производная которой на некотором промежутке X равна нулю, постоянна на этом промежутке. Доказательство: Пусть во всех точках промежутка X производная функции f(x) равна нулю, т.е f '(x) = 0. Для любых двух точек х 1, х 2 Î X по теореме Лагранжа получаем:
Так как f ' (x) = 0, то f(x2) = f(x1). Это и означает, что значения функции во всех точках промежутка одинаковы, т.е. f(x) = С, где С – некоторое число. Теорема. Если F1(x) и F2(x) - две первообразные для f(x) в некотором промежутке, то разность между ними в этом промежутке равна постоянному числу. Доказательство: Пусть, например, указанный промежуток – интервал ]а;b[. Из определения первообразной имеем: F1'(x) = f(x) и F2'(x) = f(x) для любого х Î ]а;b[. Пусть a (х) = F2(x) - F1(x). Тогда для любого х из ]а;b[ a'(х) = F2'(x) - F1'(x) = f (x) – f (x) = 0. Следовательно, согласно лемме, a (х) Подчеркнем важный факт: если производная для функции одна, т.е. операция дифференцирования однозначна, то нахождение первообразной для функции возможно лишь с точностью до некоторого постоянного слагаемого. Определение 2. Совокупность всех первообразных для функций f(x), определенных на некотором промежутке X, называется неопределенным интегралом от функции f(x) на этом промежутке и обозначается символом Таким образом, по определению,
если F'(x) = f(x). Значит, чтобы найти неопределенный интеграл от заданной функции, нужно найти какую-нибудь одну ее первообразную и прибавить к ней произвольную постоянную С. Наличие этой постоянной делает задачу нахождения функции по ее производной не вполне определенной. Отсюда происходит само название “неопределенный интеграл”. Определение 3. Нахождение первообразной для данной функции f(x) называется интегрированием функции f(x). Определение 4. Функция f(x) называется подынтегральной функцией, f(x) dх – подынтегральным выражением, х - переменной интегрирования, символ ∫ - знаком неопределенного интеграла, С – постоянной интегрирования. Пример 2. Найти D Так как x 3 =
Слово “интеграл” происходит от латинского “integer”, что означает “восстановленный”. Интегрируя какую-нибудь функцию, в примере 2 функцию x3, мы как бы восстанавливаем функцию
 Тогда геометрически неопределенный интеграл Тогда геометрически неопределенный интеграл
представляет собой семейство интегральных кривых, каждая из которых получается из любой другой кривой параллельным переносом вдоль оси Оу. Отметим без доказательства, что если функция f(x) непрерывна на некотором промежутке X, то на этом промежутке существует первообразная функции f(x), а следовательно, и неопределенный интеграл
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 73; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.161.116 (0.131 с.) |
 ,
,
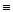 С.
С.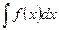 (читается: "интеграл от эф от икс де икс").
(читается: "интеграл от эф от икс де икс").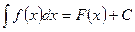 ,
,
 .
. , то функция F(x) =
, то функция F(x) =  является одной из первообразных для функции f(x) = x 3. Поэтому
является одной из первообразных для функции f(x) = x 3. Поэтому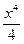 , производная которой равна x3.
, производная которой равна x3.  Определение 5. y
Определение 5. y
 Назовем график какой-либо первообразной у = F(x)
Назовем график какой-либо первообразной у = F(x) 
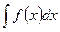 (теорема Коши).
(теорема Коши). dх =
dх = 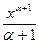 + С (a ¹-1)
+ С (a ¹-1) = x + С
= x + С = ln| х | + С
= ln| х | + С =
=  + С, а >0, а ¹1
+ С, а >0, а ¹1 = е х + С
= е х + С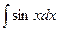 = -
= - 
 =
= 

 =
= 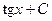
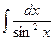 =
= 
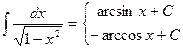

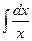 , заметим, что функция
, заметим, что функция  непрерывна в промежутках
непрерывна в промежутках  и
и  , причем в каждом из них она имеет первообразную.
, причем в каждом из них она имеет первообразную. этой первообразной, очевидно, является функция lnx, т.к.
этой первообразной, очевидно, является функция lnx, т.к. 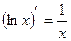 , т.е
, т.е  при
при 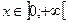 .
. первообразной по отношению к
первообразной по отношению к 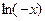 , т.е.
, т.е. при
при  . Действительно,
. Действительно,  .
.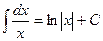 .
.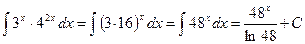 .
.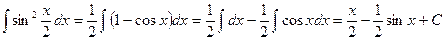 .
.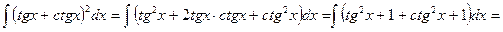
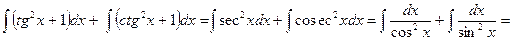
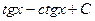 .
.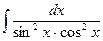 .
.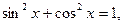 находим
находим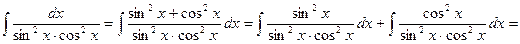
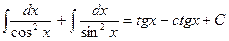 . Ñ
. Ñ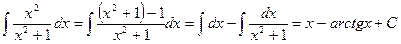 .
.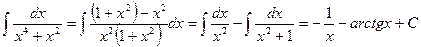 .
.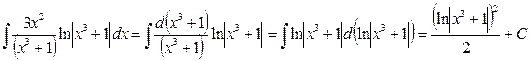 .
.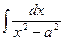 (a¹0).
(a¹0).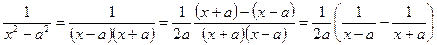 .
.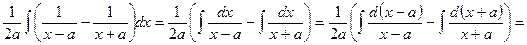
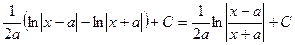 .
.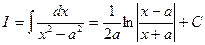 . Ñ
. Ñ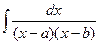 ,
, 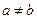 .
.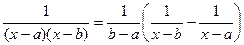 ,
,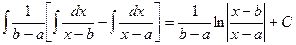 . Ñ
. Ñ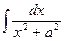 (a¹0).
(a¹0).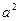 :
: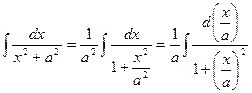 .
.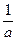 под знак дифференциала. Рассматривая
под знак дифференциала. Рассматривая 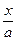 как новую переменную, получим:
как новую переменную, получим: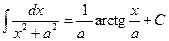 . Ñ
. Ñ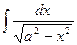 (½ х ½< а, а ¹0).
(½ х ½< а, а ¹0).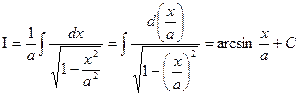 .
.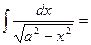
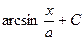 (½ х ½< а, а ¹0). Ñ
(½ х ½< а, а ¹0). Ñ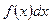 к виду
к виду 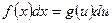 , где
, где 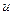 есть некоторая функция от x и g – функция более простая для интегрирования, чем f.
есть некоторая функция от x и g – функция более простая для интегрирования, чем f.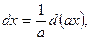
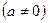
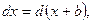 где b – постоянная величина
где b – постоянная величина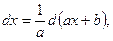
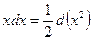 ,
,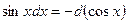 ,
,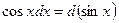 ,
,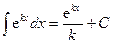 .
.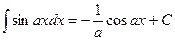 .
.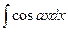 =
= 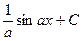 .
.
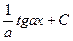 .
.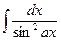 =
= 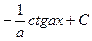 .
.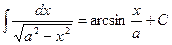 (½ х ½< а, а ¹0).
(½ х ½< а, а ¹0).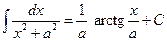 (а ¹0).
(а ¹0). под знак дифференциала эквивалентна замене переменной х на новую переменную
под знак дифференциала эквивалентна замене переменной х на новую переменную 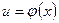 . Нижеследующие примеры иллюстрируют это положение.
. Нижеследующие примеры иллюстрируют это положение.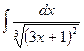 .
.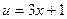 , тогда
, тогда 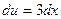 , т.е.
, т.е. 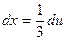 и I=
и I= 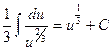 .
.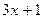 , окончательно получим
, окончательно получим 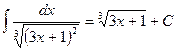 . Ñ
. Ñ .
.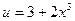 , тогда
, тогда 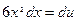 , откуда
, откуда 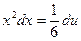 . Следовательно,
. Следовательно,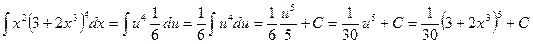 . Ñ
. Ñ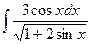 .
.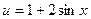 , тогда
, тогда 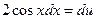 , или
, или 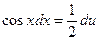 . Следовательно,
. Следовательно,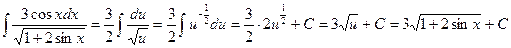 . Ñ
. Ñ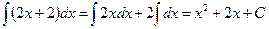 .
.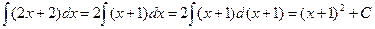 .
.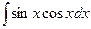 .
. .
.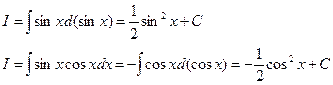
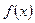 - непрерывна) не может быть непосредственно преобразован к виду табличного. Сделаем подстановку
- непрерывна) не может быть непосредственно преобразован к виду табличного. Сделаем подстановку 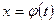 , где
, где 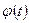 - функция, имеющая непрерывную производную. Тогда
- функция, имеющая непрерывную производную. Тогда 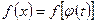 ,
, 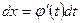 и
и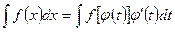 . (3)
. (3)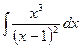 .
.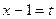 , тогда
, тогда 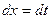 ,
, 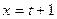 и
и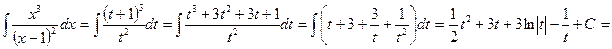
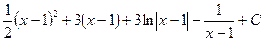 . Ñ
. Ñ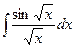 .
.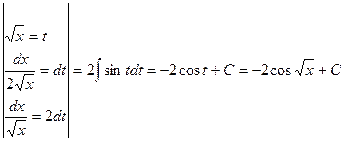 .
. 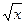 под знак дифференциала.
под знак дифференциала.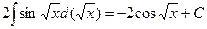 . Ñ
. Ñ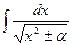 (
( ).
).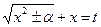 , где
, где 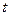 - новая переменная.
- новая переменная.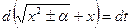 , т.е.
, т.е. 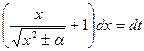 , или
, или 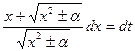 . Отсюда
. Отсюда 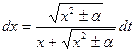 , т.е.
, т.е. 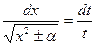 .
.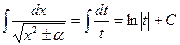 . Заменяя
. Заменяя 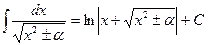 (
(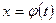 лучше выполнять замену переменной вида
лучше выполнять замену переменной вида 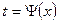 .
.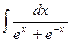 .
. ,
, 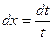 и
и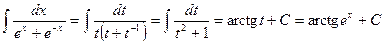 . Ñ
. Ñ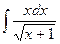 .
.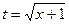 . Тогда
. Тогда 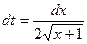 ,
, 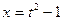 ,
, 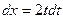 .
.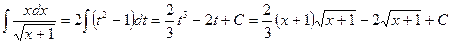 . Ñ
. Ñ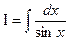 .
.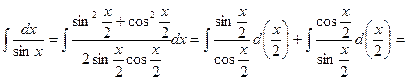
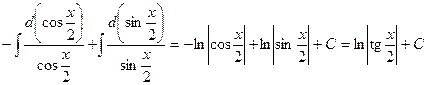 . Ñ
. Ñ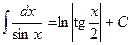 .
.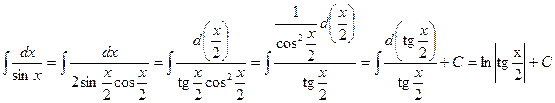 .
.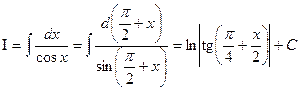 .
.


