
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принцип наименьшего действия в механике. Функция Лагранжа. Уравнение Лагранжа.
Принцип наименьшего действия Гамильтона, точнее принцип стационарности действия — способ получения уравнений движения физической системы при помощи поиска стационарного (часто — экстремального, обычно, в связи со сложившейся традицией определения знака действия, наименьшего) значения специального функционала — действия (т.е. при использовании этого принципа мы получим УРАВНЕНИЕ, при котором система движется так, чтобы минимизировать функционал – свое действие). Принцип наименьшего действия был сначала сформулирован Мопертюи в 1746 году и далее развивался (после 1748 года) математиками Эйлером, Лагранжем и Гамильтоном. Мопертюи пришёл к этому принципу из ощущения, что совершенство Вселенной требует определенной экономии в природе и противоречит любым бесполезным расходам энергии. Естественное движение должно быть таким, чтобы сделать некоторую величину минимальной. Нужно было только найти эту величину, что он и продолжал делать. Она являлась произведением продолжительности (время) движения в пределах системы на удвоенную величину, которую мы теперь называем кинетической энергией системы. Эйлер принимает принцип наименьшего количества действия, называя действие «усилием». Его выражение в статике соответствует тому, что мы теперь назвали бы потенциальной энергией. Согласно принципу наименьшего действия, каждая механическая система характеризуется определённой функцией Из курса вариационного исчисления известно, что это условие эквивалентно системе уравнений Эйлера-Лагранжа
Уравнения Эйлера — Лагранжа (в физике также уравнения Лагранжа — Эйлера или уравнения Лагранжа) являются основными формулами вариационного исчисления, c помощью которых ищутся стационарные точки (подозрительные на экстремум) и экстремумы функционалов. В частности, эти уравнения широко используются в задачах оптимизации, и, совместно с принципом стационарности действия, используются для вычисления траекторий в механике. В теоретической физике вообще это (классические) уравнения движения в контексте получения их из написанного явно выражения для действия (лагранжиана).
Использование уравнений Эйлера — Лагранжа для нахождения экстремума функционала в некотором смысле аналогично использованию теоремы дифференциального исчисления, утверждающей, что лишь в точке, где первая производная функции обращается в нуль, гладкая функция может иметь экстремум Рассмотрим замкнутую систему N материальных точек, взаимодействующих друг с другом, но ни с какими посторонними телами. Общий вид функции Лагранжа для такой системы следующий
ПОДРОБНЕЕ ПРО ДЕЙСТВИЕ: На примере физической системы с одной степенью свободы (например, материальная точка, движущаяся по прямой – т.е. траектория ее движения может быть описана уравнением с одной переменной), напомним, что действие — это функционал относительно (обобщенных) координат (в случае одной степени свободы - одной координаты q(t)), то есть выражается через q(t) так, что каждому мыслимому варианту функции q(t) сопоставляется некоторое число - действие (в этом смысле можно сказать, что действие как функционал есть правило, позволяющее для любой заданной функции вычислить вполне определенной число - также называемое действием). Действие имеет вид:
где
Действие можно вычислить для совершенно произвольной траектории q(t), какой бы «дикой» и «неестественной» она бы ни была. Однако в классической механике среди всего набора возможных траекторий существует одна-единственная, по которой тело действительно пойдёт. Принцип стационарности действия как раз и даёт ответ на вопрос, как действительно будет двигаться тело: между двумя заданными точками тело движется так, чтобы действие было стационарным. Это значит, что если задан лагранжиан системы, то мы с помощью вариационного исчисления можем установить, как именно будет двигаться тело, сначала получив уравнения движения — уравнения Эйлера — Лагранжа, а затем решив их. Это позволяет не только серьёзно обобщить формулировку механики, но и выбирать наиболее удобные координаты для каждой определенной задачи, не ограничиваясь декартовыми, что может быть очень полезно для получения наиболее простых и легко решаемых уравнений.
|
||||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 147; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.175.243 (0.007 с.) |
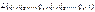 , называемая функцией Лагранжа, в краткой записи
, называемая функцией Лагранжа, в краткой записи 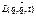 . Пусть в моменты времени t=t1, t=t2, система занимает определённые положения в пространстве, характеризуемые двумя наборами значений координат q(1) и q(2). Тогда между этими положениями система движется таким образом, чтобы интеграл
. Пусть в моменты времени t=t1, t=t2, система занимает определённые положения в пространстве, характеризуемые двумя наборами значений координат q(1) и q(2). Тогда между этими положениями система движется таким образом, чтобы интеграл 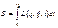 имел наименьшее возможное значение. Интеграл S называется действием. Необходимым условием минимальности S является обращение в нуль первой вариации
имел наименьшее возможное значение. Интеграл S называется действием. Необходимым условием минимальности S является обращение в нуль первой вариации 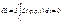
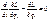 , i=1..n.
, i=1..n.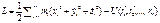 , где
, где 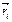 - радиус-вектор i-й точки. Функция
- радиус-вектор i-й точки. Функция 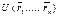 описывает взаимодействие между материальными точками и называется потенциальной энергией системы. Сумму называют кинетической энергией системы - энергией механической системы, зависящей от скоростей движения её точек. Формула кинетической энергии: mv^2 / 2, где m – масса тела, v – скорость движения тела.
описывает взаимодействие между материальными точками и называется потенциальной энергией системы. Сумму называют кинетической энергией системы - энергией механической системы, зависящей от скоростей движения её точек. Формула кинетической энергии: mv^2 / 2, где m – масса тела, v – скорость движения тела.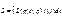
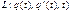 есть лагранжиан системы, зависящий от обобщённой координаты q, её первой производной по времени q’(t), а также, возможно, и явным образом от времени t. Если система имеет большее число степеней свободы n, то лагранжиан зависит от большего числа обобщённых координат
есть лагранжиан системы, зависящий от обобщённой координаты q, её первой производной по времени q’(t), а также, возможно, и явным образом от времени t. Если система имеет большее число степеней свободы n, то лагранжиан зависит от большего числа обобщённых координат 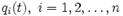 и их первых производных по времени. Таким образом, действие является скалярным функционалом, зависящим от траектории тела (по-русски: действие – это число, которое сопоставляется каждому значению функции q (t), задающей траекторию движения материальной точки).
и их первых производных по времени. Таким образом, действие является скалярным функционалом, зависящим от траектории тела (по-русски: действие – это число, которое сопоставляется каждому значению функции q (t), задающей траекторию движения материальной точки).


