
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача о распределении оборудования
Пусть V ={ J 1, J 2,…, J n } – множество работ, которые необходимо выполнить. Предположим, что для выполнения каждой работы требуется одинаковое время t и некоторые механизмы из множества механизмов М = { m 1, m 2, …, ms }. Никакие механизмы не могут быть использованы одновременно для выполнения двух и более работ. Требуется распределить механизмы так, чтобы выполнить все работы и чтобы затраченное на это время T было минимальным. Построим граф, соответствующий данной задаче, выбрав в качестве множества вершин V – множество работ. Если какие-то две работы требуют для их выполнения один и тот же механизм или механизмы, то соответствующие им вершины, соединим ребром, в противном случае – нет. Найдем какую-нибудь правильную раскраску полученного графа G. Тогда видно, что работы "раскрашенные в один и тот же цвет" могут выполняться одновременно. Значит минимальное время выполнения всех работ T = t χ (G). Аналогичным образом формулируется и интерпретируется задача о составлении расписания занятий (в школе, ВУЗе и т. д.). 2. Хроматическое число 2–дольного графа. Критерий 2-дольности
Доказательство. Необходимость. Пусть χ (G) = 2. Обозначим через V 1 все вершины графа G, раскрашенные в один цвет, а через V 2 – в другой. Поскольку между вершинами, имеющими одинаковый цвет, нет ребер, то граф G – 2-дольный с долями V 1 и V 2. Достаточность. Пусть G – 2-дольный граф. Окрасим вершины одной доли в один цвет, а другой доли – в другой цвет. Очевидно, полученная раскраска правильная и, значит, χ (G) = 2.
Доказательство. Необходимость. Пусть G – двудольный граф. Рассмотрим какой-нибудь цикл (если он существует, иначе доказывать нечего). Поскольку ребра соединяют только вершины из разных долей графа, то двигаясь по циклу мы будем поочередно переходить из одной доли в другую, пока, наконец, не вернемся в исходную вершину (и исходную долю). Поэтому цикл имеет четную длину. Достаточность. Пусть все циклы в графе G имеют четную длину. Без потери общности можно считать, что G – связный. И пусть J – некоторая вершина графа G. Обозначим, через V 1 – множество вершин графа G, расстояние от которых до вершины
соответствующими парами вершин. Обе они имеют четную длину (нечетную, если u, w Î V 2). Тогда, объединяя эти цепи и добавляя ребро { u, w }, получим цикл нечетной длины. Возможно, цепи S(u, J) и S(, J) имеют общие ребра (см. рис. 14.1). Тогда цикл получится, если удалить их из описанного объединения. Очевидно, длина его остается нечетной. Полученное противоречие завершает доказательство.
3. Некоторые оценки хроматического числа Уже отмечалось, что χ (К n) = n. Поэтому если граф G содержит полный подграф порядка r, то χ (G) ≥ r. В целом, чем меньше ребер в графе и чем меньше степени его вершин, тем меньше хроматическое число.
Доказательство. Индукция по числу вершин n графа G. База индукции: n = 2 – утверждение очевидно. Индукционный переход. Предположим, что существует правильная (r +1)– раскраска для всех графов порядка n, у которых степени вершин не превосходят r. Рассмотрим граф порядка n +1 с максимальной степенью вершин, равной r. Удалим произвольную вершину J. Для полученного графа порядка n существует согласно индукционному предположению правильная (r +1) – раскраска. Воспользуемся такой раскраской. Удаленная вершина J имеет не более r смежных, для окраски которых использовано не более r цветов. Окрасим вершину J в цвет, отличный от цвета смежных вершин (так как цветов больше, чем r, то такой цвет найдется). Получим правильную (r +1)–раскраску исходного графа.
Замечание. Оценка хроматического числа в теореме Брукса достижима (см. рис. 14.2) и, значит, не может быть в общем случае (без дополнительных предположений) улучшена. Однако, оценка весьма грубая. При выполнении условий теоремы хроматическое число может быть значительно меньше максимальной степени вершин. Например, звездный граф К 1, n , и с максимальной степенью вершин n имеет хроматическое число 2. Для колеса W 2 n по теореме Брукса χ (W 2 n ) ≤ 2 n. В действительности χ (W 2 n ) = 3.
4. Раскраски планарных графов
Доказательство. Индукция по числу вершин n. База индукции: n ≤ 7 – утверждение очевидно. Индукционный переход. Предположим, что правильная 6–раскраска существует для всякого планарного графа порядка n. Рассмотрим планарный граф порядка n +1. Согласно следствию 6 из формулы Эйлера в нем существует вершина v степени deg v ≤ 5. Удалим эту вершину. И воспользуемся 6–раскраской полученного графа, которая существует в силу индукционного предположения. Раскрасив удаленную вершину v в цвет, отличный от цветов смежных с ней вершин, получим правильную раскраску исходного графа. Замечание. С помощью более тщательных и тонких рассуждений можно доказать, что всякий планарный граф 5–раскрашиваемый. Кроме того, еще в прошлом веке была высказана гипотеза 4-х красок. Сравнительно недавно было получено положительное решение этой гипотезы с использованием ЭВМ. Пример полного графа К4, который является планарным, показывает, что эту величину (4 краски) в общем случае уменьшить нельзя. Однако, известно, что если в плоском графе нет циклов длины 3, то граф 3 – раскрашиваемый (теорема Греча), а если нет циклов нечетной длины, то достаточно 2-х красок (следует из критерия двудольности графа).
5. Реберная раскраска графа Помимо раскраски вершин рассматриваются также раскраски ребер графов. Граф G называется реберно k- раскрашиваемым, если его ребра можно раскрасить k красками так, что никакие смежные ребра не будут иметь один и тот же цвет. Наименьшее такое число k называется реберно-хроматическим числом графа G и обозначается χ e(G). Для реберно-хроматического числа справедлива
Паросочетания
1. Паросочетания Паросочетанием графа G называется любое множество попарно несмежных ребер. Паросочетание графа называется максимальным, если оно не содержится в паросочетании с большим числом ребер. Паросочетание называется наибольшим, если оно имеет наибольшее число ребер среди всех паросочетаний данного графа. Паросочетание называется совершенным, если оно покрывает все вершины графа, т. е. если каждая вершина графа G инцидентна некоторому ребру данного паросочетания. Например, для графа на рис. 15.1: · ·
· {e1, e5, e7}, {e2, e6, e9} – максимальные паросочетания, но не наибольшие; · {e1, e4, e6, e9} – наибольшее паросочетание, которое одновременно является совершенным. Совершенное паросочетание существует не для всякого графа. Чаще всего паросочетания рассматриваются в двудольных графах. В двудольном графе G с долями V 1 и V 2 совершенным паросочетанием V 1 на V 2 называется паросочетание, которое покрывает все вершины доли V 1.
К поиску соответствующих паросочетаний сводится решение некоторых классических задач.
Задача о свадьбах Пусть V = { J 1, J 2, …, J n} – множество юношей, каждый из которых знаком с некоторыми девушками из множества U = { u 1, u 2, …, um }. Требуется женить наибольшее число юношей так, чтобы каждый из них женился на знакомой ему девушке. Данная задача сводится к нахождению наибольшего паросочетания в двудольном графе G с долями V и U, в котором смежными являются вершины vi и uj, если соответствующие юноша и девушка знакомы, и не смежны – в противном случае. Возможность женить всех юношей означает существование в графе совершенного паросочетания V на U.
Задача о назначениях Имеется множество исполнителей V = { J 1, J 2, …, J n }, каждый из которых может выполнить некоторые из работ множества X = { x 1, x 2, …, xm }. Стоимость выполнения работы хi исполнителем J j равна pij. Необходимо распределить исполнителей по работам так, чтобы выполнить все работы с минимальными затратами. Ясно, что этой задаче так же отвечает соответствующий взвешенный двудольный граф. При этом возможность выполнить все работы означает существование совершенного паросочетания X на V. Для того, чтобы минимизировать затраты, необходимо искать совершенное паросочетание наименьшего веса. 2. Теорема Холла о свадьбах Пусть А – подмножество множества вершин V (G) графа G. Множество всех вершин графа G, каждая из которых смежна с некоторой вершиной из А, называется окружением множества А и обозначается NA.
Доказательство. Действительно, если для какого-то А Í V условие | NA | ≥ A не выполняется, т. е. (пользуясь терминологией задачи о свадьбах) какое-то множество юношей (предположим k человек) знакомы в совокупности меньше, чем с k девушками, то уже этих k юношей нельзя всех женить, тем более – всех юношей множества V. Таким образом необходимость данного условия очевидна.
Возможны два случая. а) Любые k юношей знакомы в совокупности не менее, чем с k +1 девушкой. Тогда, рассуждая по индукции по числу юношей (база индукции очевидно имеется) женим произвольного юношу на знакомой ему девушке. Для остальных юношей, количество знакомых девушек уменьшается не более, чем на 1. Значит, для любого числа k любые k юношей будут знакомы не менее, чем с k девушками. По индукционному предположению их можно женить.
б) Существует k юношей, у которых ровно k знакомых девушек (k < n = | A |). По предположению индукции их можно женить. Остается n-k юношей. Для них по- прежнему будет выполняться условие, что любые l из них знакомы не менее, чем с l девушками. Действительно, если бы это было не так, то соответствующие l юношей вместе с предыдущими k имели бы в совокупности не менее l + k знакомых девушек, что противоречит условию теоремы. Значит, и оставшихся n-k юношей можно женить по индукционному предположению.
Сети
1. Основные понятия Сетью (в самом общем смысле) называется всякий граф, в котором специально выделены некоторые вершины, называемые полюсами. Например, корневое дерево можно рассматривать как однополюсную сеть (полюс – корень). В данном параграфе под сетью мы будем понимать взвешенный ориентированный граф. Примерами таких сетей являются схемы улиц, нефте-, газо- и трубопроводов, линий электропередач (в качестве веса может выступать пропускная способность); схемы выполнения комплекса работ при подготовке какого-либо мероприятия, проекта, строительства дома, завода и т. д. (вес – время выполнения работ или их стоимость, в зависимости от решаемой задачи). Для сетей полустепень исхода deg + v вершины v определяется как сумма весов всех дуг, для которых v является началом, а полустепень захода всех дуг, для которых v является концом. deg - v – сумма весов Как и для обычных орграфов, для сетей справедлива
В сети вершины, которые являются только началом дуг, называются источниками, а вершины, которые являются только концами дуг – стоками (это полюса сети). Обычно рассматриваются сети без ориентированных циклов. В этом случае они представляют собой совокупность путей, ведущих от источников к стокам. Кроме того, можно считать, что в сети существует один источник и один сток. В противном случае, если сеть имеет несколько источников v 1, v 2,..., v s и несколько стоков w 1, w 2,..., w t, то сеть можно преобразовать, объединив все источники и объединив все стоки, или ввести фиктивный (общий) источник v 0 и сток w 0, как показано на рис. 16.1.
Сеть с одним источником v 0 и одним стоком w 0 называют (v 0, w 0)-сетью.
2. Потоки в сетях Для данной сети (G, p) потоком называется функция
j (e), ставящая в соответствие каждой дуге e некоторое неотрицательное число, такое что: 1) 0 £ j (e) £ p (e) (т.е. поток неотрицателен и не превосходит пропускной; способности данной дуги); 2) для всякой вершины u, кроме источника и стока å j (e k) = å j (e n), где первая e k en сумма вычисляется по всем дугам e k, для которых вершина u является концом, а вторая сумма по всем ребрам
e n, для которых u является началом (т. е. общий поток, втекающий в данную вершину, равен суммарному потоку, вытекающему из этой вершины). Дуги, для которых поток равен пропускной способности: j (e) = p (e), называются насыщенными; в противном случае, если j (e) < p (e) – ненасыщенными. Из леммы о "рукопожатиях" и условия 2) следует, что суммарный поток, вытекающий из источника v 0, равен суммарному потоку, втекающему в сток w 0. Эта величина называется величиной потока (v 0, w 0)-сети. Две (v 0, w 0) цепи графа G называют реберно-непересекающимися, если у них нет общих ребер. Две (v 0, w 0) цепи графа G называют вершинно-непересекающимися, если у них нет общих вершин, за исключением v 0, w 0. Основная задача, которая ставится для вышеописанных сетей, состоит в отыскании максимального потока данной сети, т.е. потока, величина которого наибольшая при условиях 1) – 2). Решение этой задачи связано предварительно с ответом на несколько более простых вопросов, касающихся связного (неориентированного) мультиграфа G и фиксированной пары его вершин v 0 и w 0: 1. Сколько существует реберно-непересекающихся простых (v 0, w 0)- цепей в графе G? 2. Сколько существует вершинно-непересекающихся простых (v 0, w 0)- цепей в графе G? Для того, чтобы сформулировать ответы на эти вопросы, введем следующие определения. Множество A Ì E (G) называется (v 0, w 0)- разделяющим, если всякая простая (v 0, w 0)-цепь содержит ребро из множества А. Множество B Ì V (G) называется (v 0, w 0)- отделяющим, если всякая простая (v 0, w 0)-цепь содержит вершину из В.
(v 0, w 0)-цепей в графе G равно минимальному числу вершин в (v 0, w 0)-отделяющем множестве графа G.
дугам простых (v 0, w 0)-цепей в (v 0, w 0)-сети равно минимальному числу дуг в (v 0, w 0)- разделяющем множестве цепи.
Схема доказательства. Если пропускные способности p (e) всех дуг выражаются целыми положительными числами, то расщепим каждую дугу е на p (e) параллельных дуг с пропускной способностью 1. И тогда утверждение теоремы следует из теоремы о целочисленности. Если пропускные способности p (e)Î Q для всех ребер е сети, то умножив их все на общий знаменатель, придем к предыдущему случаю. Если p (e) не являются рациональными, то воспользуемся аппроксимацией действительных чисел рациональными, т. е. заменим p (e) последовательностями a n (e) рациональных чисел, такими, что lim a n (e) = p (e) при n ® ¥. Для каждого n и сети с пропускными способностями an имеем предыдущий случай, при котором утверждение теоремы верно. Переходя к пределу при n ® ¥, получим, что теорема справедлива в общем случае. 3. Сетевое планирование Предположим, что для осуществления некоторого проекта необходимо выполнить определенный комплекс работ. Построим сетевой график этих работ. Вершины сети (события) будем отождествлять с их номерами, обозначив номером 0 источник (начало работ). Завершающему событию, т. е. окончанию всех работ, которое является стоком сети, присвоим наибольший номер n, в то время, как остальные промежуточные события пронумеруем от 0 до n -1, принимая, насколько это возможно, во внимание очередность их наступления. Если некоторое событие j может наступить только после события i и при этом должна быть выполнена определенная работа, то построим дугу (i, j), присвоив ей вес tij – время выполнения соответствующей работы. Если событие j не может наступить раньше события i, но для этого не требуется выполнение специальной работы, то также построим дугу (i, j) и присвоим ей вес 0. По сетевому графику определим время, необходимое на выполнение всего проекта. Рассмотрим всевозможные (0, n)-пути от начала работ до их окончания. Для каждого пути подсчитаем его длину (время выполнения всех работ данного пути). Простой (0, n)-путь, имеющий наибольшую длину, называется критическим путем сети. Понятно, что время, необходимое на выполнение всех работ проекта, не может быть меньше длины (времени) критического пути. Верно и обратное, что этого времени достаточно для выполнения проекта. Таким образом, справедлива
Работы, лежащие на критическом пути, также называются критическими. Сокращение или увеличение сроков выполнения критических работ соответственно сокращает или увеличивает общую продолжительность выполнения проекта. Остальные работы называются некритическими и допускают некоторое запаздывание в их выполнении, которое не задерживает сроков реализации всего проекта.
|
|||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 132; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.74.44 (0.079 с.) |
 Утверждение. Пусть G – некоторый непустой граф. Тогда χ(G) = 2 в том и только том случае, когда G – 2-дольный граф.
Утверждение. Пусть G – некоторый непустой граф. Тогда χ(G) = 2 в том и только том случае, когда G – 2-дольный граф. Теорема. (критерий 2-дольности). Граф двудольный тогда и только тогда, когда он не имеет циклов нечетной длины.
Теорема. (критерий 2-дольности). Граф двудольный тогда и только тогда, когда он не имеет циклов нечетной длины.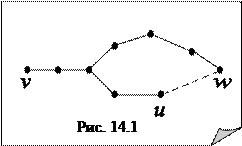 J являются четными (в частности J Î V 1), а через V 2 – остальные вершины графа. Достаточно показать, что если вершины u, Î V 1 (или V 2), то они не являются смежными. Предположим противное, что существует ребро{ u, }. Рассмотрим кратчайшие цепи S(u, J) и S(, J) между
J являются четными (в частности J Î V 1), а через V 2 – остальные вершины графа. Достаточно показать, что если вершины u, Î V 1 (или V 2), то они не являются смежными. Предположим противное, что существует ребро{ u, }. Рассмотрим кратчайшие цепи S(u, J) и S(, J) между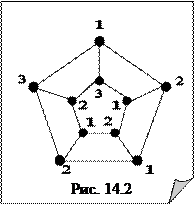
 Теорема (Брукс). Пусть G – связный граф, не являющийся полным, и степени всех вершин которого не превосходят r, где r ≥ 3. Тогда χ (G) ≤ r.
Теорема (Брукс). Пусть G – связный граф, не являющийся полным, и степени всех вершин которого не превосходят r, где r ≥ 3. Тогда χ (G) ≤ r. Теорема. Для любого планарного графа существует правильная 6–раскраска.
Теорема. Для любого планарного графа существует правильная 6–раскраска. Теорема (Визниг). Пусть G – мультиграф, максимальная степень вершин которого равна r. Тогда r ≤ χ e(G) ≤ r +1.
Теорема (Визниг). Пусть G – мультиграф, максимальная степень вершин которого равна r. Тогда r ≤ χ e(G) ≤ r +1. {e1, e2, e6} – не является паросочетанием;
{e1, e2, e6} – не является паросочетанием;


 Теорема. В двудольном графе G с долями V и U существует совершенное паросочетаиие V на U тогда и только тогда, когда для любого А Í V мощность | NA | ≥ A.
Теорема. В двудольном графе G с долями V и U существует совершенное паросочетаиие V на U тогда и только тогда, когда для любого А Í V мощность | NA | ≥ A. Докажем достаточность. Пусть " А Í V условие | NA | ≥ A выполняется.
Докажем достаточность. Пусть " А Í V условие | NA | ≥ A выполняется. Лемма (о "рукопожатиях"). Сумма полустепеней исхода всех вершин сети равна сумме полустепеней захода.
Лемма (о "рукопожатиях"). Сумма полустепеней исхода всех вершин сети равна сумме полустепеней захода.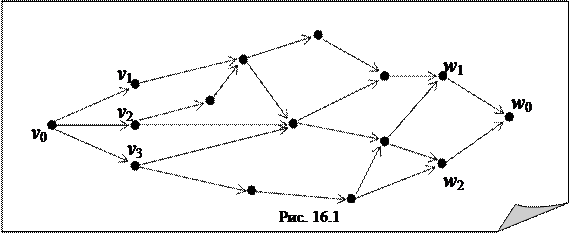
 Теорема 1 (Менгер). Максимальное число реберно-непересекающихся простых (v 0, w 0)-цепей в графе G равно минимальному числу ребер в (v 0, w 0)-разделяющем множестве графа G.
Теорема 1 (Менгер). Максимальное число реберно-непересекающихся простых (v 0, w 0)-цепей в графе G равно минимальному числу ребер в (v 0, w 0)-разделяющем множестве графа G. Теорема 2 (Менгер). Максимальное число вершинно-непересекающихся
Теорема 2 (Менгер). Максимальное число вершинно-непересекающихся Теорема 3 (о целочисленности). Максимальное число непересекающихся по
Теорема 3 (о целочисленности). Максимальное число непересекающихся по Теорема 4 (Форд - Фалкерсон). Величина максимального потока в (v 0, w 0)-сети равна минимальной пропускной способности (v 0, w 0)-разреза сети. (Пропускная способность разреза подсчитывается как сумма пропускных способностей всех ребер, составляющих данный разрез).
Теорема 4 (Форд - Фалкерсон). Величина максимального потока в (v 0, w 0)-сети равна минимальной пропускной способности (v 0, w 0)-разреза сети. (Пропускная способность разреза подсчитывается как сумма пропускных способностей всех ребер, составляющих данный разрез).


