Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Множества и операции над нимиСтр 1 из 6Следующая ⇒
1. Основные понятия Понятие множества, как и некоторые другие исходные понятия в математике, не определяется. Ему дается описание, которое иллюстрируется примерами. Под множеством в математике понимается любая совокупность каких-либо объектов. При этом сами объекты, составляющие множество, называются элементами множества. Например, можно говорить о множестве яблок в мешке, множестве натуральных чисел, множестве геометрических фигур на плоскости и т. д. Как правило, множество объединяет однотипные элементы (яблоки, числа и т.д.). Но это – не обязательно. Можно рассматривать множества, состоящие из разнородных элементов. Обычно множества обозначают заглавными латинскими буквами (A, B, C, …), а их элементы – прописными (a, b, c, …). Если A – множество, а a – его элемент, то пишут: a Î A. Если b не является элементом множества B, то пишут: b Ï B. Примеры. 1. М 1 — множество действительных чисел R. 2. М 2 — множество решений уравнения sin x = 1.
3. М 3
— множество чисел вида p + 2p k, где 2 k Î Z (Z - множество целых чисел). 4. М 4 — футбольная команда «БАТЭ-Борисов» (т.е., множество футболистов этой команды). 5. М 5 — множество всех футбольных команд высшей лиги. 6. М 6 — множество русских слов из словаря В. И. Даля. 7. М 7 — множество равносторонних треугольников. 8. М 8 — множество равноугольных треугольников. Множество B называется подмножеством множества A, если всякий элемент множества B принадлежит множеству A. В этом случае пишут: B Í A. Множества A и B называются равными, если их элементы совпадают. Легко видеть, что равенство множеств A = B имеет место тогда и только тогда, когда B Í A и A Í B. Именно в проверке последних двух условий заключается основной способ доказательства равенства двух множеств. Примеры: М 2 = М 3; М 7 = М 8. Если B Í A, но A ¹ B, то B называется собственным подмножеством множества A, и это записывается: B Ì A.
Множество мощности 0, т.е. не содержащее никаких элементов, называется пустым множеством и обозначается: Æ. Принято считать, что пустое множество является подмножеством любого множества A, поскольку невозможно указать ни одного элемента Æ, который бы не принадлежал множеству A. Нетрудно видеть, что справедлива
Лемма. Пустое множество единственно. Доказательство. Действительно, если Æ1, Æ2 — два пустых множества, то согласно вышеотмеченному свойству пустого множества (быть подмножеством любого множества) имеем: Æ 1 Í Æ 2 и Æ2 Í Æ1, откуда Æ 1 = Æ 2.
2. Способы задания множеств Множество считается заданным, если о каждом элементе можно однозначно сказать, принадлежит он этому множеству или нет. а) Простейший способ задания множества состоит просто в перечислении всех элементов данного множества. Если множество A конечное, состоящее из элементов a 1, a 2, …, a n, то пишут A = { a 1, a 2, …, a n}. В частности, { a } — множество, состоящее из одного элемента a. Но такой способ задания применим, разумеется, лишь к конечным множествам. б) Другой, универсальный способ: задание множества A с помощью характеристического свойства элементов данного множества, то есть такого свойства, которым обладают все элементы множества A и не обладают другие элементы, не принадлежащие A. Если P (x) — такое свойство, то пишут: A = { x | P (x) }. Например, для конечного множества A = { a 1, a 2,…, a n} можно записать: A = { x | x = a 1, или x = a 2, или …, или x = a n}. Множество всех депутатов парламента можно задать тьак: D = { x | x — депутат}. Множество всех студентов S = { x | x — студент}. в) Еще один способ — это задание множества с помощью порождающей процедуры, или алгоритмический способ. Например, пусть M = {1, 2, 4, 8, 16,…} — множество степеней числа 2. Тогда его можно задать так: 1) 1Î M; 2) если x Î M, то 2 x Î M. Другой пример: множество М p = {314, 159, 256, 358, …} задается как последовательность троек подряд идущих цифр десятилетней записи числа p = 3,141592653589793238462…. (В действительности, учитывая трансцендентность числа p, множество М p содержит все целые числа от 0 до 999.) г) Четвертый способ — задание множеств с помощью операций над уже известными множествами. К описанию свойств, задающих множество, естественно предъявить требования точности и недвусмысленности. Например, множество хороших фильмов 2009г. разные люди зададут разными списками. Даже сами критерии отбора фильмов могут оказаться различными.
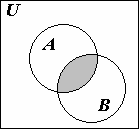
Надежный способ точного описания множества — распознающая (разрешающая) процедура. Например, для множества степеней двойки М 2 n разрешающей процедурой может служить разложение числа на простые множители. Задание множества М 4 нельзя отнести ни к одному из перечисленных способов; оно по сути совсем не задано, а только названо. Задать его можно списком футболистов, или описанием: М 4 есть множество лиц, имеющих удостоверение футболиста клуба «БАТЭ-Борисов». В этом случае разрешающая процедура — это проверка документов. 3. Операции над множествами Во всех рассуждениях о нескольких множествах удобно считать, что они являются подмножествами некоторого более широкого множества U, которое называется универсальным. На практике, как правило, универсальное множество даже явно не указывается, а ясно из контекста, или в случае необходимости может быть легко установлено. Определение 1. Пересечением двух множеств A и B называется множество A Ç B, состоящее из элементов, которые принадлежат каждому из множеств A и B, т.е. A Ç B = { x | x Î A и x Î B }. Например, {1; 2; 5; 7} Ç {1; 5; 6} = {1; 5}. Пересечением множества прямоугольников с множеством ромбов является множество квадратов. Пересечением множества студентов-первокурсников с множеством отличников является множество первокурсников-отличников. Определение 2. Объединением множеств A и B называется множество A È B, состоящее из элементов, которые принадлежат хотя бы одному из множеств A или B: A È B = { x | x Î A или x Î B }. Например, {1; 2; 5} È {1; 5; 6; 7} = {1; 2; 5; 6; 7}. Аналогично определяются операции объединения и пересечения трех, четырех, любой совокупности множеств. При этом используются следующие обозначения. Если S = { A 1, A 2, …} — совокупность множеств, то их объединение и k k пересечение обозначаются: U A, I A; или U A i , I A i – для конечных совокупностей A Î S
A Î S i =1 i =1 и A i , i =1 A i i =1 — для бесконечных совокупностей; а также A i,
A i, где I —
некоторое множество индексов. Определение 3. Разностью множеств A и B называется множество A \ B, состоящее из всех элементов множества A, не принадлежащих множеству B: A \ B = { x | x Î A и x Ï B }.
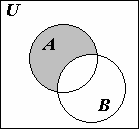
Если ясно, о каком универсальном множестве U идет речь, то разность U \ A называется дополнением множества A и обозначается: A. Например, разностью множества четных чисел и множества чисел, кратных 3, является множество четных чисел, не делящихся на 6. Дополнением множества четных чисел в (универсальном множестве целых чисел) является множество нечетных чисел. Диаграммы Эйлера-Венна
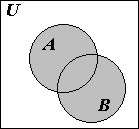
Введенные операции допускают удобное графическое истолкование с помощью диаграмм (или кругов) Эйлера-Венна, где результат операции указан штриховкой (рис.1.1).
Рис. 1.1 Разбиения множеств В основе всевозможных классификаций в биологии, лингвистике, других науках и сферах деятельности человека лежит понятие разбиения множества на попарно пересекающиеся части.
Определение 4. Пусть A — некоторое множество и X i, i Î I система подмножеств из A, обладающая следующими свойствами:
i Î I б) X i Ç X j = Æ " i ¹ j. Тогда говорят, что множество { X i, i Î I } является разбиением множества A. Примеры. Разбиение списка студентов группы по первым буквам их фамилий. Разбиение студентов группы по вариантам на контрольной работе. Разбиение целых чисел на четные и нечетные. Вообще, для любого множества A, множества на две части.
U = A È A — разбиение универсального Замечание. Для любого a Î A, если X i = A
— разбиение множества A, то существует единственное множество X i, такое что a Î X i.
4. Свойства операций над множествами. Алгебра множеств Операции È и Ç обладают свойствами, аналогичными сумме и произведению чисел. В связи с этим их зачастую также называют суммой и произведением множеств и обозначают соответственно A + B, AB вместо A È B и A Ç B. Действительно, для любых множеств A, B и C справедливы следующие равенства:
В справедливости этих законов легко убедиться с помощью диаграмм Эйлера- Венна, изобразив отдельно множества, соответствующие левой и правой части равенства, и проверив, что они совпадают. Например, для иллюстрации закона 7) имеем диаграммы, приведенные на рис. 1.2.
заштриховано
Рис. 1.2 (A È B)Ç (A È C)
Строгое доказательство всех равенств основано на проверке включений Í и Ê. Например, для доказательства закона 9) нужно проверить: 9а) 9б)
A È B Í A Ç B;
A Ç B Í A È B. Доказательство 9а). Пусть
x Î A È B. Тогда x Ï A È B. Значит, x Ï A и x Ï B, то есть
x Î A и
x Î B, и поэтому
x Î A Ç B. Доказательство 9б). Пусть
x Î A Ç B. Тогда
x Î A и
x Î B. Следовательно, x Ï A и x Ï B. Поэтому x Ï A È B и, значит,
x Î A È B. Определение. Совокупность Ù(U) всех подмножеств универсального
 множества U (такая совокупность называется булеаном множества U) вместе с операциями È, Ç, и ×, обладающими вышеперечисленными свойствами, называется булевой алгеброй множеств. множества U (такая совокупность называется булеаном множества U) вместе с операциями È, Ç, и ×, обладающими вышеперечисленными свойствами, называется булевой алгеброй множеств.
Заметим, что в результате операций È, Ç, и × над любыми подмножествами из U также получаются подмножества из U. В этом случае говорят, что указанные операции замкнуты на U.
5. Декартово произведение множеств Пусть имеется два множества A и B (не обязательно
А ¹ B). Определение. Декартовым (или прямым) произведением множеств A и B называется множество всех упорядоченных пар вида (a, b), где первый элемент a Î A, а второй — b Î B: A ´ B = {(a, b) | a Î A, b Î B }. Множества A и B предполагаются непустыми. В противном случае, если A = Æ или B = Æ, то A ´ B = Æ. Если, например, A = { a 1, a 2}, B = { b 1, b 2, b 3}, то: A ´ B = {(a 1, b 1), (a 1, b 2), (a 1, b 3), (a 2, b 1), (a 2, b 2), (a 2, b 3)}. Вообще говоря, A ´ B ¹ B ´ A, за исключением случая, когда A = B. Тогда
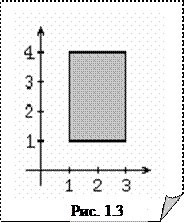
A 2. Если A = B = R – множество действительных чисел, то R 2 = {(a, b) | a, b Î R } можно рассматривать, как координатную плоскость, отождествив пару (a, b) с точкой, имеющей координаты x = a и y = b. В частности, если имеются отрезки A = [1; 3], B = [1; 4], то A ´ B представляет собой прямоугольник на координатной плоскости xОy (рис. 1.3). Всякая кривая Г на плоскости может быть истолкована как подмножество R 2, определяемое некоторым условием (уравнением): Г = {(x, y) Î R | f (x, y) = 0}. Аналогично определяется декартовое произведение любого количества непустых множеств. Именно, пусть заданы множества A 1, A 2, …, A n. Тогда n -кой (кортежем) называется упорядоченный набор (a 1, a 2, …, a n), такой что a i Î A i
" i = 1, n. Множество всех таких n -ок называется декартовым произведением множеств A 1, A 2, …, A n и
обозначается A 1 ´ A 2 ´K´ A n
= Õ A i i =1
. В частности, если все A i = A, то n
i i =1 называется n -ой декартовой степенью множества A. Замечание. Вообще говоря, (R 4 )3 ¹ R12 . Действительно, (R 4 )3
следует рассматривать как множество матриц матричной структуры. 3´ 4, а R 12 — кортежи, не учитывающие Таким образом, уже из данного примера следует, что ассоциативный закон для декартового произведения множеств не выполняется. Но дистрибутивные законы относительно È, Ç и \ имеют место: (A 1 È A 2 )´ B = (A 1 ´ B)È (A 2 ´ B); (A 1 Ç A 2 )´ B = (A 1 ´ B)Ç (A 2 ´ B); (A 1 \ A 2 )´ B = (A 1 ´ B) \ (A 2 ´ B). В любом случае, операция “ ´” существенно отличается от предшествующих операций на множествах в том плане, что декартово произведение множеств из данного универсального множества U уже не принадлежит U.
Отображения множеств
1. Основные понятия Пусть X и Y – непустые множества. Если каждому элементу х Î Х ставится в соответствие единственный элемент y Î Y, то говорят, что задано отображение множества Х во множество Y. Часто не делают различий между понятием “отображение” и “функция”, однако функциями чаще всего называют отображения числовых множеств. Если ¦ – отображение множества Х в Y, то пишут: ¦: Х ® Y или Х ⎯⎯ f ® Y. Элемент y Î Y, который ставится в соответствие элементу х Î Х при отображении ¦: Х ® Y, называется образом элемента х при отображении ¦. При этом пишут: y = f (x) или ¦: х a y. Элемент х в свою очередь называется прообразом y при отображении ¦. Определение 1. Два отображения ¦: Х ® Y и g: X ® Y называются равными, если f (x) = g (x) для любого х Î Х. Определение 2. Пусть задано отображение ¦: Х ® Y и А Ì Х. Образом множества А при отображении ¦ называется совокупность образов всех элементов множества А. Образ A обозначается: ¦(А).
Определение 3. Пусть ¦: Х ® Y и А Ì Х. Отображение, которое каждому элементу х Î А, рассматриваемому как элемент из Х, ставит в соответствие f (x)Î Y,
Таким образом, f A: A ® Y, причём f A (x) = f (x) " х ÎА. Обратно, при
В случае, если Х и Y – конечные множества, то отображение ¦: Х ® Y может быть задано таблицей соответствий, состоящей из двух строк. ⎛ x 1 x 2 x 3 ⎞ Например, для X = { x 1 , x 2 , x 3 }, Y = { y 1, y 2 } запись f = ⎜ ⎝ y 1 y 2 ⎟ y 1 ⎠ означает, что f (x 1 ) = y 1 , f (x 2) = y 2, f (x 3 ) = y 1 . Упражнение: Выпишите все различные отображения ¦: Х ® Y в указанном примере и определите их количество. Найдите количество различных отображений ¦: Х ® Y, если | X | = n, а | Y | = m. Важным примером таких отображений служат подстановки из n элементов: ⎛ 1 2 3 ... n ⎞
⎝ 1 2 d3 ... ⎟ , где {d1 , d 2 ,..., d n }= {1, 2 ,...,n }. d n ⎠ Другие примеры отображений: - поворот плоскости вокруг начала координат на угол a; - проецирование 3-мерного пространства на координатную плоскость xОy; - ¦: R ® R, ¦(x) = sin x. Определение 4. Отображение ¦: Х ® Y называется инъективным (взаимно однозначным), если различным элементам множества Х соответствуют различные образы из Y, т.е., если x 1 ¹ x 2 Þ f (x 1 ) ¹ f (x 2 ). Легко видеть, что это условие равносильно следующему: f (x 1) = f (x 2) Þ x 1 = x 2. Например, подстановки, повороты плоскости – взаимно однозначные отображения; проецирование R 3 ® R 2 – не взаимно однозначное. Отображение f: R ® R, где f (x) = sin x – не взаимно однозначное, но f: ⎡- p ; p ⎤ ® R, где f (x) = sin x – взаимно однозначное. ⎣⎢ 2 2 ⎥⎦ Определение 5. Отображение ¦: Х ® Y называется сюръективным, если каждый элемент y Î Y является образом для некоторого элемента х Î X, т.е. если каждый элемент y Î Y имеет хотя бы один прообраз. Понятно, что ¦: Х ® Y – сюръективно тогда и только тогда, когда f (X) = Y. Например, подстановки, поворот на угол a, проецирование R 3 ® R 2 – сюръективны. Отображение f: R ® R, где f (x) = sin x – не сюръективно, но f: R ® [- 1; 1], f (x) = sin x – сюръективно. Определение 6. Отображение ¦:Х®Y называется биективным, если оно одновременно и инъективно и сюръективно. Примеры. Подстановки; поворот на угол a; f: ⎡- p ; p ⎤ ® [- 1;1 ]; f (x) = sin x;
g: R ® R, ⎢⎣ 2 g (x) = 2 x + 1 – биективные отображения. 2 ⎥⎦
2. Произведение (композиция) отображений Пусть ¦: Х ® Y, g: Y ® Z и пусть х Î Х. Отображение ¦ переводит х в некоторый элемент y Î Y . При этом элемент y под действием отображения g переходит в некоторый элемент z из Z. Таким образом, в результате последовательного выполнения сначала ¦ а потом g, каждый элемент х Î Х отображается в элемент z Î Z и мы получаем отображение h: X ® Z. Определение 7. Произведением отображений ¦: Х ® Y и g: Y ® Z называется отображение gf: X ® Z определяемое равенством (gf)(x) = g ( f (x)) . Например, пусть f (x) = sin x, g (x) = 2 x. Тогда ( fg)(x) = sin(2 x), (gf )(x) = 2sin x. Отметим, что не всегда gf и fg определены одновременно. Для этого необходимо, чтобы g (Y) Í X. В частности, если f: X ® X, g: X ® X, то gf и fg
равны. Теорема 1. Если ¦: Х ® Y, g: Y ® Z, h: Z ® U, то h (gf) и (hg) f определены и Доказательство. Так как gf: X ® Z, то h (gf): X ® U. Аналогично, hg: Y ® U, поэтому (hg) f: X ® U. Покажем, что " х Î Х [ h (gf)](x) = [(hg) f ](x) . Пусть x 0 Î X. Имеем:
отображений [ h (gf)](x 0 ) = h [(gf)(x 0 )] = h [ g ( f (x 0 ))] = h [ g (y 0 )] = h (z 0 ) = u 0 и [(hg) f ](x 0 ) = hg ( f (x 0 )) = h (g ( f (x 0 ))) = ...... = u 0 . Определение 8. Отображение f: X ® X называется тождественным, или единичным, если f (x) = x, " х Î Х. Обозначения: eX, 1 X, id X.
f: X ® Y, то f e X = f и e Y f = f.
f: X ® X, то f e X = e X f = f.
Если ¦ и g сюръективны, то fg – сюръективно. Доказательство. 1) Имеем f (x 1 ) = f (x 2 ) Þ x 1 = x 2 ; g (y 1 ) = g (y 2 ) Þ y 1 = y 2. Пусть (gf)(x 1 ) = (gf)(x 2 ) , т.е. g (f (x 1 )) = g (f (x 2 )) Þ f (x 1 ) = f (x 2 ) Þ x 1 = x 2. 2) Пусть f, g – сюръективны и z 0 Î Z. Так как g – сюръективно, то $ y 0: g (y 0) = z 0. А так как ¦ – сюръективно, то $ z 0 = g (y 0 ) = g ( f (x 0 )) = (gf)(x 0 ) . x 0 : f (x 0 ) = y 0. Таким образом,
3. Обратные отображения Определение. Пусть f: X ® Y. Если существует отображение j: Y ® X такое, что j f = e X и f j = e Y, то отображение j называется обратным к отображению ¦, а отображение ¦ в этом случае называется обратимым. Понятно, что в условиях определения обратным к j является ¦. Обозначение: j = f -1.
Отображение f: X ® Y обратимо тогда и только тогда, когда оно биективно. Доказательство. Необходимость. Пусть отображение f: X ® Y биективно. Так как оно сюръективно, то " y 0 Î Y есть хотя бы один прообраз из Х. Но в силу инъективности все элементы имеют разные образы. Поэтому y0 имеет единственный прообраз х0. Сопоставив каждому элементу y из Y его единственный прообраз, получим отображение j : Y ® X такое, что если y = f (x), то j(y) = x. При этом получим " х Î Х j f (x) = j ( f (x)) = j (y) = x, т.е. j f = e X; " y Î Y f j (y) = f (j (y)) = f (x) = y, т.е. f j = e Y. Достаточность. Пусть отображение f: X ® Y – обратимое и j : Y ® X – обратное к ¦. Пусть f (x 1 ) = f (x 2 ). Применим к данному равенству отображение j: j ( f (x 1 )) = j ( f (x 2 )) Û (j f)(x 1 ) = (j f)(x 2 ) Û e x (x 1 ) = e x (x 2 ) Û x 1 = x 2 . Таким образом, ¦ – инъективно. Пусть y 0 Î Y. Найдём прообраз х 0, такой, что y 0 = f (x 0 ) . Имеем: y 0 = e Y (y 0 ) = ( f j )(y 0 ) = f (j (y 0 )) = f (x 0 ), где x 0 = j(y 0) . Тем самым, ¦ – сюръективно.
Отношения
1. Основные понятия и способы задания отношений В различных научных и других сферах деятельности человека для описания связей между предметами используется понятие отношения. Например, отношение “меньше – больше” на множестве действительных чисел; отношение делимости на множестве целых чисел; отношение подобия на множестве треугольников; отношения параллельности и перпендикулярности на множестве прямых и плоскостей; отношения родства, дружбы, знакомства на множестве людей; отношение “начальник- подчиненный” на предприятии и др. В математике понятие отношения, как и большинство понятий, имеет строгое определение. Определение. Бинарным отношением R на множествах A и B называется всякое подмножество R Í A ´ B. Если элементы a Î A и b Î B находятся в отношении R, т. е. (a, b) Î R, то пишут: aRb. Например, a < b (для отношения “меньше – больше” на множестве действительных чисел), a M b (a делится на b, для отношения делимости на множестве целых чисел), A Í B (для отношения включения на множестве подмножеств некоторого универсального множества U), множестве треугольников) и т. д. Ä ABC ~ Ä KLM (для отношения подобия на Если B = A, то отношение R Í A ´ A называется отношением на множестве А (вместо «отношение на множествах А и А»). Отношение U=A ´ B, называется универсальным, или всюду истинным отношением на A и B. Отношение R = Æ называется пустым, или всюду ложным. Отношение I = {(a, a) | a Î A }называется тождественным отношением на множестве A. Множество D (R) = { a Î A | $ b Î B, aRb } называются областью определения отношения R, а множество E (R) = { b Î B | $ a Î A, aRb } – областью значений отношения R. (D (R) и E (R) иногда называют также проекциями R на A и B, соответственною.)
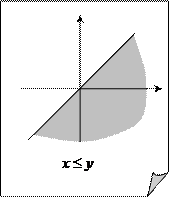
Если Два отношения R 1 и R 2 называются равными, если R 1 и R 2 равны, как множества. R 1 Í R 2, то говорят, что "отношение R 1 влечет отношение R 2" (или "из отношения R 1 следует отношение R 2"). Отношения на числовых множествах можно изобразить графически на координатной плоскости, поставив каждой паре (a, b) Î R в соответствие точку с координатами x = a и y = b. Например, отношению “ £ ” на множестве действительных чисел R соответствует полуплоскость (рис. 3.1). Отношению “=” на множестве действительных чисел R соответствует прямая (рис. 3.2).
Рис. 3.1 Рис. 3.2 Рис. 3.3
Всякое отображение (функцию) f: A ® B можно рассмотреть как отношение R f на множествах А и В, положив aR f b, если f (a) = b для всех a Î A, b Î B. Если А и В – числовые множества, то графической иллюстрацией такого отношения является обычный график функции y = f (x) (рис. 3.3). Обратно, всякое отношение
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 120; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.26.176 (0.388 с.) |

 Множества могут быть конечными и бесконечными. Число элементов конечного множества A называется его мощностью и обозначается A.
Множества могут быть конечными и бесконечными. Число элементов конечного множества A называется его мощностью и обозначается A.

 A
A
 A = A
A = A



 A È A = U
A È A = U
 A È (B Ç C)
A È (B Ç C)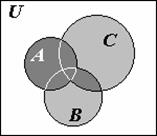 заштриховано дважды
заштриховано дважды








 произведение A ´ А называется декартовым квадратом множества A и обозначается:
произведение A ´ А называется декартовым квадратом множества A и обозначается:
 Итак, f (A) = { f (x) x Î A }. Ясно, что f (A) Ì f (X).
Итак, f (A) = { f (x) x Î A }. Ясно, что f (A) Ì f (X).

 называется сужением отображения ¦ на А и обозначается f A.
называется сужением отображения ¦ на А и обозначается f A. выполнении этих условий ¦: Х ® Y является продолжением отображения f A: A ® Y.
выполнении этих условий ¦: Х ® Y является продолжением отображения f A: A ® Y. определены. Но даже в этом случае равенство fg = gf, вообще говоря, не выполняется (это видно из рассмотренного примера), Таким образом, умножение отображений не коммутативно. Однако оно ассоциативно.
определены. Но даже в этом случае равенство fg = gf, вообще говоря, не выполняется (это видно из рассмотренного примера), Таким образом, умножение отображений не коммутативно. Однако оно ассоциативно. Теорема 2. Если
Теорема 2. Если Следствие. Если
Следствие. Если Теорема 3. Пусть ¦: Х ® Y, g: Y ® Z. Если ¦ и g инъективны, то fg – инъективно.
Теорема 3. Пусть ¦: Х ® Y, g: Y ® Z. Если ¦ и g инъективны, то fg – инъективно. Следствие. Произведение биективных отображений – биективно.
Следствие. Произведение биективных отображений – биективно. Теорема 4 (критерий обратимости отображения).
Теорема 4 (критерий обратимости отображения). Следствие. Если ¦ – биективно, то и ¦-1 также биективно.
Следствие. Если ¦ – биективно, то и ¦-1 также биективно.