
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Крива. Обчислення довжини дуги кривої
Нехай точка Визначимо довжину Означення 4.1. Шляхом або кривою параметричними рівняннями кривої. Так, наприклад, криву − півкруг (рис.7) можна записати декартовим рівнянням
Відмітимо, що рівняння У подальшому параметри Означення 4.2. Крива Якщо 1) граничні точки кривої 2) будь-які не граничні точки кривих то крива Проста замкнена плоска крива Відмітимо, що крива
Зрозуміло, що ця крива є об’єднання чотирьох простих кривих, визначених на окремих проміжках Означення 4.3. Нехай функції Кажуть, що рівняння (4.1) параметрично визначають криву Так, рівняння параметрично визначає криву Нехай тепер крива
Означення 4.4. Якщо множина Існують приклади неспрямляємих кривих, які можна знайти, наприклад, в Теорема. (Достатня ознака умови існування довжини дуги кривої і формули для її обчислення). Якщо функції Доведення. Оскільки функції
За умовою Якщо через звідки і слідує, що множина Відмітимо, що для даного розбиття Відмітимо, що для спрямляємості кривої необхідна лише обмеженість
Одержимо формули обчислення довжини дуги кривої, визначеної різними способами. Розглянемо задачу обчислення довжини графіка функції Аналогічно, якщо потрібно обчислити довжину дуги кривої Якщо крива а значить, за формулою (4.2) маємо
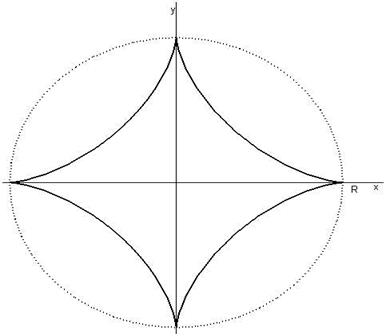
Приклад 4.1 Обчислити довжину дуги астроїди (рис. 9). Так називають криву, параметричні рівняння якої
Рис. 9 Розв'язання. Зрозуміло, що достатньо обчислити довжину дуги кривої, коли де А тому Приклад 4.2. Обчислити довжину дуги кривої, визначеної полярним рівнянням
Рис. 10
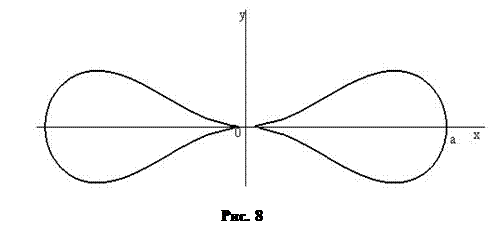
Розв'язання. За формулою (2.5) і враховуючи симетрію графіка, маємо де Остаточно Приклад 2.3 Обчислити довжину еліпса, визначеного канонічним рівнянням Розв'язання. Враховуючи параметричні рівняння еліпса де Інтеграл не виражається в елементарних функціях, як зазначалось і раніше. Його називають еліптичним. За допомогою таблиць значень функції Зауваження. Якщо крива в просторі
то довжина дуги кривої де
|
||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 139; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.122.162 (0.032 с.) |
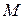 рухається на площині
рухається на площині 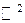 і відомий закон її руху
і відомий закон її руху 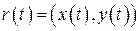 , де
, де 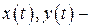 прямокутні декартові координати точки
прямокутні декартові координати точки 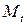 в момент часу
в момент часу 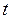 .
.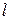 шляху, який пройде точка
шляху, який пройде точка 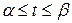 .
.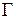 називають відображення
називають відображення 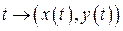 числового проміжку в просторі
числового проміжку в просторі 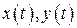 на проміжку
на проміжку 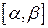 . При цьому
. При цьому 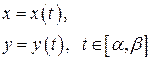 (4.1)
(4.1)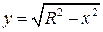 , а також параметричними рівняннями
, а також параметричними рівняннями 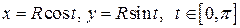 .
.
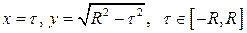 , також визначають той самий півкруг.
, також визначають той самий півкруг.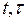 такі, що
такі, що 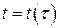 або
або 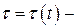 неперервні і строго зростаючі функції.
неперервні і строго зростаючі функції.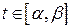 відповідають різні точки
відповідають різні точки 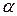 і
і 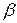 параметра
параметра 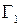 і
і 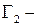 дві прості криві такі, що
дві прості криві такі, що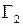 ;
;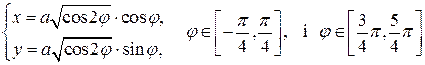 .
.
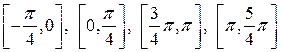 .
.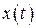 і
і 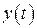 неперервні на множині
неперервні на множині 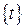 , де
, де 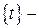 інтервал, сегмент, півсегмент.
інтервал, сегмент, півсегмент.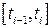 , яка розбиває множину
, яка розбиває множину 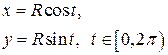
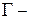 коло радіуса
коло радіуса 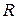 з центром в
з центром в 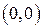 .
.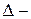 довільне розбиття
довільне розбиття 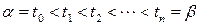 . Позначимо через
. Позначимо через 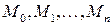 відповідні точки кривої
відповідні точки кривої 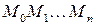 будемо називати ломаною, вписаною в криву
будемо називати ломаною, вписаною в криву 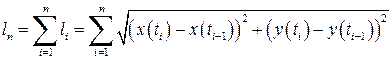 .
.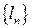 довжин вписаних в криву
довжин вписаних в криву 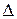 сегмента
сегмента 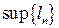 ) називається довжиною дуги кривої
) називається довжиною дуги кривої 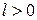 .
.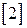 .
. (4.2)
(4.2)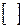 ), то
), то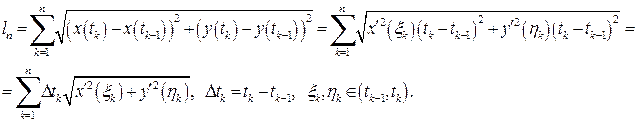
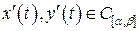 , тому вони обмежені на
, тому вони обмежені на 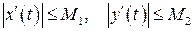
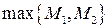 , то
, то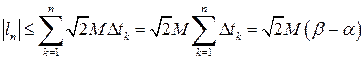 ,
,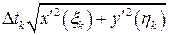 не є інтегральною сумою для функції
не є інтегральною сумою для функції 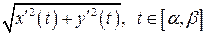 тому, що точки
тому, що точки 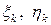 нав’язані теоремою Лагранжа, і, крім того, на відрізку
нав’язані теоремою Лагранжа, і, крім того, на відрізку 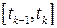 вибирається довільним чином одна точка, а не дві
вибирається довільним чином одна точка, а не дві 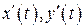 на
на 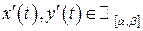 .
.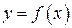 , визначеної на
, визначеної на 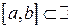 . Відмітимо, що графік функції є крива в
. Відмітимо, що графік функції є крива в 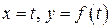 , то із (4.2) одержимо
, то із (4.2) одержимо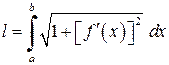 (4.3)
(4.3)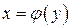 на відрізку
на відрізку 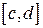 , то
, то 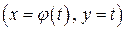
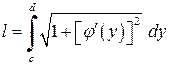 (4.4)
(4.4)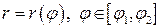 , де
, де  параметр і
параметр і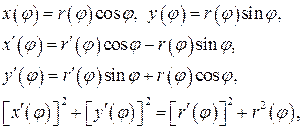
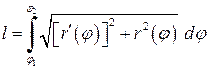 (4.5)
(4.5)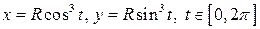 .
.
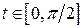 (більш того, з урахуванням симетрії відносно прямої
(більш того, з урахуванням симетрії відносно прямої 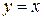 можна взяти
можна взяти 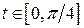 ):
):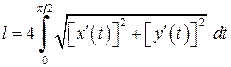 ,
,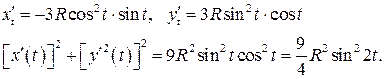
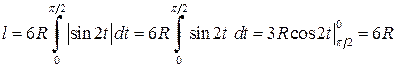 .
.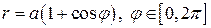 (рис. 10, кардіоїда).
(рис. 10, кардіоїда).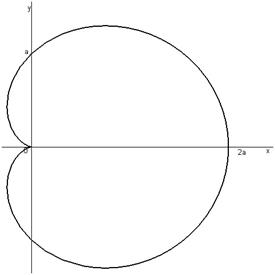
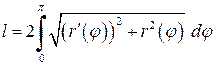 ,
,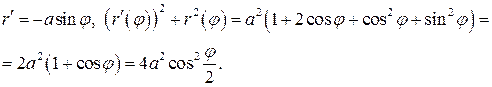
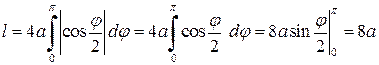 .
.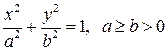 .
.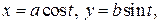
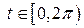 , одержимо
, одержимо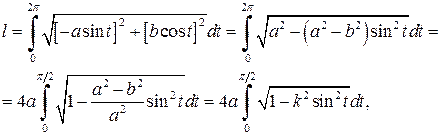
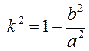 .
.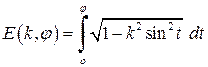
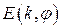 маємо: довжина еліпса дорівнює
маємо: довжина еліпса дорівнює 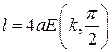 .
.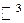 визначається параметричними рівняннями
визначається параметричними рівняннями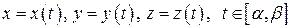 , (4.6)
, (4.6)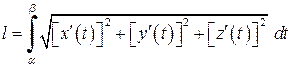 , (4.7)
, (4.7)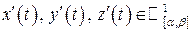 .
.


