
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Застосування визначеного інтеграла до задач геометрії та розв’язку задач з фізики та механікиСтр 1 из 4Следующая ⇒
Розд іл ІІІ
Застосування визначеного інтеграла до задач геометрії та розв’язку задач з фізики та механіки
Поняття плоскої множини
Розглянемо множину Точку Множину всіх граничних точок називають границею множини Множина відкрита множина, область (круг з центром у точці Плоска множина Множину Із курсу елементарної математики відомо як знайти площу прямокутника, трикутника, трапеції тощо. Нехай тепер Послідовність Означення. Обмежена область Можна проводити розбиття не обов’язково квадратами, а, наприклад, прямокутниками, трапеціями. Приклад не квадровної плоскої обмеженої фігури приводиться, наприклад, в Справедлива наступна теорема, доведення якої можна прочитати
Теорема. Для того, щоб плоска фігура була квадровною, необхідно і достатньо, щоб для будь-якого
Площа поверхні обертання
Передусім зупинимось, що розуміють під цім терміном. Нехай
Проведемо розбиття де Можна довести, що коли Відмітимо, що можна одержати (7.1) і за ослабленою умовою: Приклад 7.1. Знайти площу поверхні еліпсоїда обертання.
Розв'язання. Нехай еліпс
Якщо Приклад 7.2. Обчислити площу тора (див. приклад. 6.3 розділу ІІІ).
Розв'язання. Зрозуміло, що У даному випадку Під знаком інтеграла необмежена функція і зрозуміло, що він не існує в традиційному сенсі. Чи означає це, що тор немає площі? Поки це свідчить лише про те, що вибране параметричне представлення півкола не задовольняє умові
Тому Площа поверхні тора дорівнює довжині кола
Розд іл ІІІ
Застосування визначеного інтеграла до задач геометрії та розв’язку задач з фізики та механіки
Поняття плоскої множини
Розглянемо множину Точку Множину всіх граничних точок називають границею множини Множина відкрита множина, область (круг з центром у точці Плоска множина Множину Із курсу елементарної математики відомо як знайти площу прямокутника, трикутника, трапеції тощо. Нехай тепер Послідовність Означення. Обмежена область Можна проводити розбиття не обов’язково квадратами, а, наприклад, прямокутниками, трапеціями. Приклад не квадровної плоскої обмеженої фігури приводиться, наприклад, в Справедлива наступна теорема, доведення якої можна прочитати Теорема. Для того, щоб плоска фігура була квадровною, необхідно і достатньо, щоб для будь-якого
|
||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 74; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.255.116 (0.041 с.) |
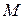 точок
точок 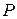 площини
площини 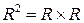 . Околом точки
. Околом точки 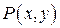 називають будь-який круг площини, який містить точку
називають будь-який круг площини, який містить точку 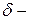 околом цієї точки називають круг радіуса
околом цієї точки називають круг радіуса 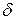 з центром в точці
з центром в точці 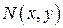 називається зовнішньою точкою множини
називається зовнішньою точкою множини 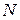 , який не містить жодної точки із
, який не містить жодної точки із 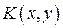 називається граничною точкою множини
називається граничною точкою множини 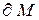 .
.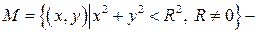
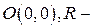 радіус),
радіус), 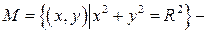 її границя.
її границя.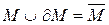 називають замкненою.
називають замкненою. обмежена плоска область. Розіб’ємо її прямими
обмежена плоска область. Розіб’ємо її прямими 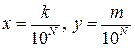 , де
, де 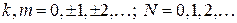 .
. 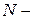 називають рангом розбиття. Так, розбиття
називають рангом розбиття. Так, розбиття 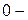 го рангу
го рангу 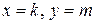 містить квадрати зі сторонами довжини
містить квадрати зі сторонами довжини 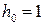 . Позначимо через
. Позначимо через 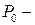 сукупність квадратів, сторони яких мають довжину
сукупність квадратів, сторони яких мають довжину 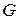 , а через
, а через 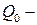 сукупність квадратів, які містять
сукупність квадратів, які містять 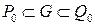 і при цьому площу або міру
і при цьому площу або міру 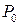 та
та 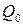 легко обчислити,
легко обчислити, 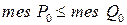 . Аналогічно, розглядаючи розбиття
. Аналогічно, розглядаючи розбиття 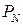 та
та 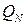 , причому
, причому 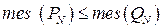 і
і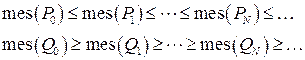
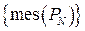 обмежена зверху, а
обмежена зверху, а 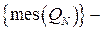 знизу, а тому існують
знизу, а тому існують
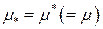 і число
і число  називають площею або мірою області
називають площею або мірою області 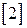 .
.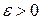 можна вказати такий описаний навколо фігури
можна вказати такий описаний навколо фігури 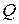 і такий вписаний в фігуру
і такий вписаний в фігуру 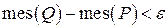
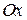 графіка функції
графіка функції 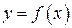 , заданої на відрізку
, заданої на відрізку 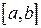 (рис.15).
(рис.15).
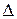 відрізку
відрізку 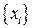 і нехай
і нехай 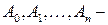 відповідні точки графіка функції
відповідні точки графіка функції 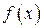 . Побудуємо ломану
. Побудуємо ломану 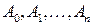 . При обертанні її навколо осі
. При обертанні її навколо осі 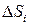 елемента поверхні обертання відповідно
елемента поверхні обертання відповідно 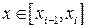 приблизно дорівнює
приблизно дорівнює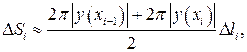
 довжина відрізка
довжина відрізка 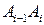 , а значить
, а значить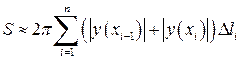 .
.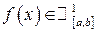 , то поверхня, одержана обертанням кривої
, то поверхня, одержана обертанням кривої 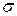 обчислюється за формулою
обчислюється за формулою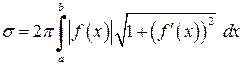 . (7.1)
. (7.1)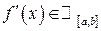 .
.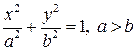 обертається навколо осі
обертається навколо осі 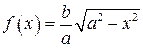 , ексцентриситет
, ексцентриситет 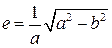 і за формулою (7.1) маємо
і за формулою (7.1) маємо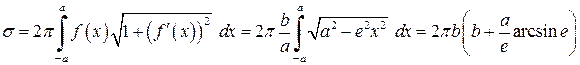 .
.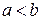 , то, як неважко перевірити,
, то, як неважко перевірити, 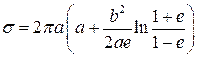 .
.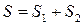 , де
, де  площа поверхні яка одержана обертанням графіка функції
площа поверхні яка одержана обертанням графіка функції 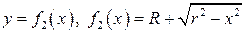 , а
, а 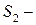 площа поверхні яка одержана обертанням графіка функції
площа поверхні яка одержана обертанням графіка функції 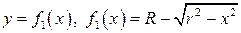 ,
, 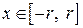 , навколо осі
, навколо осі 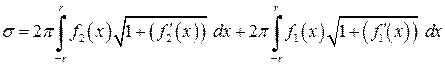 .
.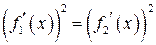 ,
, 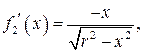
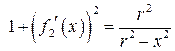 і
і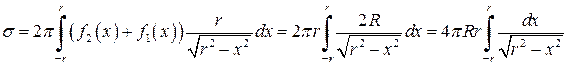 .
.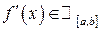 . Поставлена задача потребує розширення поняття інтеграла Рімана і про це ми поговоримо в темі — невласні інтеграли. А щоб завершити розв’язок задачі використаємо параметричне рівняння півкола
. Поставлена задача потребує розширення поняття інтеграла Рімана і про це ми поговоримо в темі — невласні інтеграли. А щоб завершити розв’язок задачі використаємо параметричне рівняння півкола 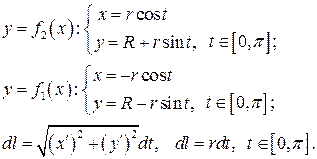
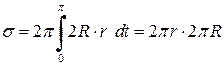 .
.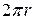 помноженій на путь
помноженій на путь 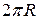 , який проходить центр тяжіння при одному оберті навколо осі обертання. − І знову одержали наслідок з відомої теореми Гульдіна.
, який проходить центр тяжіння при одному оберті навколо осі обертання. − І знову одержали наслідок з відомої теореми Гульдіна.


