
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проекции ускорения точки на естественные оси.
47 Пусть точка движется по криволинейной траектории и в момент времени Представив скорость, как Выясним кинематический смысл слагаемых правой части. С первой составляющей все понятно, модуль этого составляющего ускорения равен Рассмотри вторую составляющую, т.е. определяем модуль и направление вектора
Разделив Найдем величину угла между векторами
48
Оба вектора Т.о. проекция ускорения на направление скорости равна производной от модуля скорости по времени, а проекция ускорения на главную нормаль равна отношению квадрату скорости к радиусу кривизны траектории в той же точке, где в данный момент находится движущаяся точка.
Рассмотрим как определяется ускорение точки для частных случаев движения. 1. Равномерное прямолинейное движение.
2. Неравномерное прямолинейное движение.
3. Равномерное криволинейное движение.
Неравномерное криволинейное движение. 49
Используя связь между координатным и естественным способами задания движения точки, можно вывести зависимости, связывающие проекции ускорения на естественные и декартовые оси. Из зависимости (37) Из зависимости (38), с учетом (32) и (39), получаем выражение для нормального ускорения точки
Из зависимости (38) с учетом (41), получим выражение для радиуса кривизны
Кинематика твердого тела
|
|||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 134; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.101.91 (0.011 с.) |

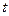 она занимает положение
она занимает положение 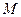 и имеет скорость
и имеет скорость  , а в момент
, а в момент 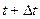 - положение
- положение 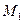 и имеет скорость
и имеет скорость  . Длину элементарной дуги
. Длину элементарной дуги  обозначим
обозначим 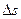 .
. и учитывая зависимость (26) получаем выражение для ускорения
и учитывая зависимость (26) получаем выражение для ускорения 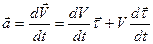 .
.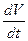 и направлен этот вектор по направлению орт вектора
и направлен этот вектор по направлению орт вектора  , т.е. по касательной. Эта составляющая ускорения называется касательным или тангенциальным ускорением и обозначается
, т.е. по касательной. Эта составляющая ускорения называется касательным или тангенциальным ускорением и обозначается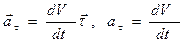 (37)
(37) 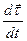 .
. 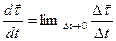 , где
, где 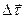 - разность векторов
- разность векторов 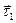 и
и 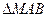 до параллелограмма
до параллелограмма  (рис. 54). Вектор
(рис. 54). Вектор 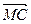 представляет собой разность векторов
представляет собой разность векторов  .
.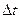 получим новый вектор
получим новый вектор  , направленный по прямой
, направленный по прямой  . Выясним направление этого вектора в пределе при
. Выясним направление этого вектора в пределе при 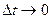 . Как было указано в предыдущем параграфе, плоскость параллелограмма
. Как было указано в предыдущем параграфе, плоскость параллелограмма  . Треугольник
. Треугольник 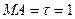 ,
, 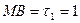 (рис. 55). Угол при вершине
(рис. 55). Угол при вершине 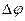 . Получаем
. Получаем 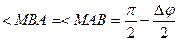 , а поэтому
, а поэтому 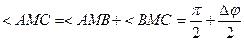 . Отсюда заключаем, что в пределе при
. Отсюда заключаем, что в пределе при  угол
угол 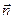 , значит
, значит . Определяем модуль этого вектора
. Определяем модуль этого вектора 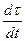 . Из треугольника
. Из треугольника 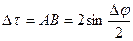 , тогда
, тогда  . Переходим к пределу
. Переходим к пределу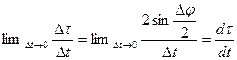 . Тогда
. Тогда  .
. . Окончательно
. Окончательно  . Тогда
. Тогда  . Этот вектор также полностью определен, по модулю он равен
. Этот вектор также полностью определен, по модулю он равен 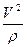 и направлен по главной нормали к центру кривизны, с учетом орт вектора
и направлен по главной нормали к центру кривизны, с учетом орт вектора  (38)
(38) 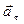 и
и  лежат в соприкасающейся плоскости, значит и итоговый вектор
лежат в соприкасающейся плоскости, значит и итоговый вектор  лежит в этой же плоскости, а проекция этого вектора на бинормаль равна нулю
лежит в этой же плоскости, а проекция этого вектора на бинормаль равна нулю 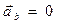 .
. (39)
(39)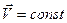 ,
,  ,
,  ,
,  ,
, 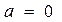
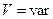 ,
,  ,
, 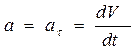 ,
, 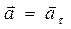
 ,
,  ,
, 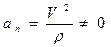 ,
,  ,
, 
 ,
,  ,
, 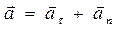 .
. (40)
(40) (41)
(41) (42)
(42)


