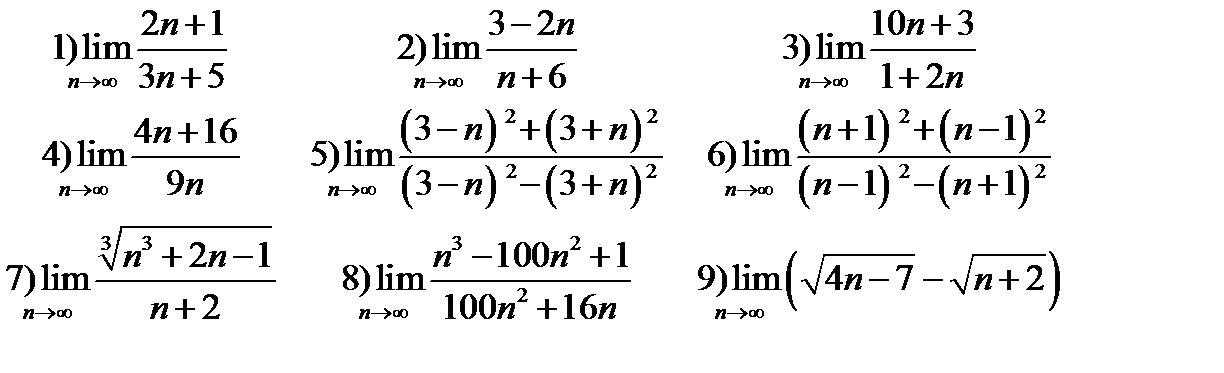Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм для решения системы линейных уравнений методом ГауссаСтр 1 из 4Следующая ⇒
СОДЕРЖАНИЕ Введение
Общие требования для студентов по выполнению практических работ
Показатели оценивания работ
Требования к технике безопасности при выполнении практических работ
Практическая работа №1. Решение систем линейных уравнений различными методами Практическая работа №2. Предел функции. Вычисление производной функции. Исследование и построение графиков функций с помощью производной Практическая работа №3. Неопределенный интеграл.Методы нахождения неопределенного интеграла. Определенный интеграл. Приложение определенного интеграла к решению прикладных задач. Практическая работа №4. Элементы теории вероятностей. Дискретная и непрерывная случайные величины. Закон распределения случайной величины. По заданному условию построить закон распределения дискретной случайной величины.
Список литературы ………………………………………….
Введение Методические указания по организации и выполнению практических работ разработаны согласно рабочей программы учебной дисциплины математика и требованиям к результатам обучения Федерального государственного образовательного стандарта среднего профессионального образования по специальности 13.02.11 «Техническая эксплуатация и обслуживание электромеханического и электрического оборудования (по отраслям)» (заочной формы обучения) Практические работы направлены на освоение следующих результатов обучения: умения: - решать прикладные задачи в области профессиональной деятельности; знания: -значение математики в профессиональной деятельности и при освоении профессиональной образовательной программы; -основные математические методы решения прикладных задач в области профессиональной деятельности; -основные понятия и методы математического анализа, линейной алгебры, теории комплексных чисел, теории вероятностей и математической статистики; основы интегрального и дифференциального исчисления
На выполнение каждой работы отводится два часа аудиторнойнагрузки Общие требования для студентов по выполнению Практических работ
1. Перед выполнением практической работы необходимо повторить теоретический материал, используя рекомендованную литературу, конспект лекций и теоретическую часть работы.
2. Студенты обязаны иметь при себе линейку, карандаш, калькулятор, тетрадь для выполнения (или для оформления отчетов) практических работ. 3. Отчеты по практическим работам оформляются аккуратно и должны включать в себя следующие пункты: · название работы и ее цель; · описание этапов выполнения работы (записываются требуемые теоретические положения, расчеты, заполнение требуемых таблиц и построение графиков и т.д.). · вывод. 4. При подготовке к сдаче практической работы, необходимо ответить на предложенные контрольные вопросы. 5. Если отчет по работе не сдан до выполнения следующей работы по неуважительной причине, оценка за работу снижается.
Показатели оценивания работ При оценивании практической работы учитывается следующее: - качество самостоятельного выполнения практической части работы (соблюдение методики выполнения, получение результатов в соответствии с целью работы и т.д.); - качество оформления отчета по практической работе (в соответствии с требованиями приведенными выше); - качество устных ответов на контрольные вопросы при защите работы (глубина ответов, использование специальной терминологии, знание методики выполнения работы и т.д.).
Критерии оценки: Ответ оценивается отметкой «5», если: работа выполнена полностью; в логических рассуждениях и обосновании решения нет пробелов и ошибок; в решении нет математических ошибок (возможны некоторые неточности, описки, которая не является следствием незнания или непонимания учебного материала). Отметка «4» ставится в следующих случаях: работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки); допущены одна ошибка, или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки). Отметка «3» ставится, если: допущено не более двух ошибок или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если: допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере. Преподаватель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
Требования к технике безопасности при выполнении Практических работ - Вход в аудиторию осуществляется только по разрешению преподавателя. - На первом занятии преподаватель проводит первичный инструктаж по технике безопасности и напоминает студентам о бережном отношении к оборудованию и о материальной ответственности каждого из них за сохранность оборудования и обстановки. - При обнаружении повреждений оборудования персональную ответственность несут студенты, выполнявшие работу на этом оборудовании. Виновники обязаны возместить материальный ущерб. - Если во время проведения работы на оборудовании замечены какие-либо неисправности оборудования, необходимо немедленно сообщить об этом преподавателю. - После окончания работы рабочее место следует привести в порядок.
Практическая работа № 1 Тема Решение систем линейных уравнений различными методами Цель работы: Используя теоретический материал и образцы решения, закрепить навыки решения задач по теме «Решение систем линейных алгебраических уравнений различными способами»
В результате выполнения работы студенты осваивают следующие результаты обучения в соответствии с ФГОС СПО: умения: - решать прикладные задачи в области профессиональной деятельности; знания: -значение математики в профессиональной деятельности и при освоении профессиональной образовательной программы; -основные понятия и методы математического анализа, линейной алгебры, теории комплексных чисел, теории вероятностей и математической статистики; Порядок выполнения работы: 1. Повторите теоретические положения по теме и записать определение, формулы расчета и т.п. 2. Выполните задание, согласно своего варианта. Исходные данные возьмите в приложении. 3. Сделайте выводы по результатам работы Теоретическая часть 1. Пусть дана система линейных уравнений
Коэффициенты a11,12,..., a1n,..., an1 , b2,..., bn считаются заданными. Вектор -строка íx1, x2,..., xn ý - называется решением системы (1), если при подстановке этих чисел вместо переменных все уравнения системы (1) обращаются в верное равенство. Определитель n-го порядка D=çAê=ça ij ç, составленный из коэффициентов при неизвестных, называется определителем системы (1). В зависимости от определителя системы (1) различают следующие случаи: a) Если D¹, то система (1) имеет единственное решение, которое может быть найдено по формулам Крамера: x1= определитель n-го порядка Di (i=1,2,...,n) получается из определителя системы путем замены i-го столбца свободными членами b1 , b2 ,..., bn. б) Если D=, то система (1) либо имеет бесконечное множество решений, либо несовместна,т.е. решений нет.
2. Рекомендации по выполнению заданий 1. Рассмотрим систему 3-х линейных уравнений с тремя неизвестными.
1. В данной системе составим определитель
2. Составить и вычислить следующие определители:
3. Воспользоваться формулами Крамера. Практическое значение правила Крамера для решения системы n линейных уравнений с п неизвестными невелико, так как при его применении приходится вычислять п +1 определителей n -го порядка: D, D x 1, D x 2, …, D xn. Более удобным является так называемый метод Гаусса. Он применим и в более общем случае системы линейных уравнений, т. е. когда число уравнений не совпадает с числом неизвестных.
Более удобным является так называемый метод Гаусса. Он применим и в более общем случае системы линейных уравнений, т. е. когда число уравнений не совпадает с числом неизвестных. Итак, пусть дана система, содержащая m линейных уравнений с п неизвестными: а11х1 + а12х2 + …+ а1 n хn = b1; а21х1 + а22х2 + …+ а2 n хn = b2; . …………………………………… аm1х1 + аm2х2 + …+ аm n хn = bm Метод Гаусса решения системы заключается в последовательном исключении переменных. Основные понятия Квадратное уравнение с действительными коэффициентами и отрицательным дискриминантом не имеет действительных корней. Поэтому приходится расширять множество действительных чисел, добавляя к нему новые числа. Эти новые числа вместе с действительными числами образуют множество, которое называют множеством комплексных чисел. Комплексное число – это выражение вида где x, y – вещественные числа, а Числом, сопряженным к Тригонометрическая форма комплексного числа. Каждому комплексному числу вида (1.1) можно поставить в соответствие точку M(x;y) на декартовой плоскости (при этом на оси OX располагаются вещественные числа
Модулем комплексного числа назовем длину отрезка называется тригонометрической формой записи комплексного числа. Преобразуем (1.1)
и, сравнивая с (1.2), получаем, что аргумент z можно найти, решив систему Возведение в степень и извлечение корней. Если комплексное число задано тригонометрической формой Для извлечения корня n -й степени (n – целое число, большее 1) из комплексного числа, заданного в тригонометрической форме, применяется формула, дающая n значений этого корня:
Контрольные вопросы (Задания для самопроверки качества освоенных результатов обучения) - понятие определителя n-ого порядка; - методы решения систем линейных уравнений; - решение систем линейных уравнений методом Крамера; - формулы Крамера; - решение систем линейных уравнений методом Гаусса; - понятие алгебраического дополнения; - понятие транспонированной матрицы; - метод обратной матрицы.
Требования к содержанию отчета по работе Отчёт о работе должен содержать название и цель работы, задание, результаты выполнения задания. По результатам работы необходимо сделать выводы.
Вариант№ 0 Задание 1.Решение системы линейных уравнений методом Крамера
Проверка:
Задание 2. Решить методом Гаусса систему уравнений x 1 – 2 x 2 + x 3 + x 4 = –1; 3 x 1 + 2 x 2 – 3 x 3 – 4 x 4 = 2; 2 x 1 – x 2 + 2 x 3 – 3 x 4 = 9; x 1 + 3 x 2 – 3 x 3 – x 4 = –1.
Решение:Составим матрицу В и преобразуем ее. Для удобства вычислений отделимвертикальной чертой столбец, состоящий из свободных членов: 1 –2 1 1 –1 B = 3 2 –3 –4 2 2 –1 2 –3 9 1 3 –3 –1 –1
Умножим первую строку матрицы В последовательно на 3, 2 и 1 и вычтем соответственно из второй, третьей и четвертой строк. Получим матрицу,эквивалентную исходной:
1 –2 1 1 –1 0 8 –6 –7 5 0 3 0 –5 11
0 5 –4 –2 0
Третью строку матрицы умножим на 3 и вычтем ее из второй строки. Затем новую вторую строку умножим на 3 и на 5 и вычтем из третьей и четвертой строк. Получим матрицу, эквивалентную исходной:
1 –2 1 1 –1 0 –1 –6 8 –28 0 0 –1 0 –3 0 0 0 19 –19
Из коэффициентов последней матрицы составим систему, равносильную исходной:
x 1 – 2 x 2 + x 3 + x 4 = –1; – X 2 – 6 x 3 + 8 x 4 = –28; – x 3 = –3; 19 x 4 = –19.
Решим полученную систему методом подстановки, двигаясь последовательно от последнего уравнения к первому. Из четвертого уравнения x 4 = –1, из третьего х 3 = 3. Подставив значения х3 и x 4 во второе уравнение, найдем x2 = 2. Подставив значения x 2, x3, x4 в первое уравнение, найдем x 1 = 1. Ответ. (1; 2; 3;-1).
Задание 3. Решить систему уравнений методом обратной матрицы.
Решение: Введем обозначения:
Теперь исходную систему уравнений можно записать в виде матричного уравнения. A * X = B Умножим (слева) левую и правую часть уравнения на A-1 - матрицу обратную матрице A. A -1 * A * X = A -1 * B Согласно определению обратной матрицы: A -1 * A = E E * X = A -1 * B Согласно определению единичной матрицы: E * X = X X = A -1 * B задача сводится к нахождению обратной матрицы A -1
Ответ: x1 = -11/8 x2 = 9/4 Задание 4. Сложить и умножить комплексные числа Решение. Для сложения чисел производим следующие вычисления:
Теперь умножаем:
Ответ.5+5i, 2+11i
Приложение:
ВАРИАНТ 1 Задание 1. Найти решение систем линейных уравнений методами Крамера, Гаусса, обратной матрицы:
Задание 2. Вычислить, выписать вещественную и мнимую части полученных комплексных чисел.
ВАРИАНТ 2 Задание 1. Найти решение систем линейных уравнений методами Крамера, Гаусса, обратной матрицы:
Задание 2. Вычислить, выписать вещественную и мнимую части полученных комплексных чисел.
ВАРИАНТ 3 Задание 1. Найти решение систем линейных уравнений методами Крамера, Гаусса, обратной матрицы:
Задание 2. Вычислить, выписать вещественную и мнимую части полученных комплексных чисел.
ВАРИАНТ 4 Задание 1. Найти решение систем линейных уравнений методами Крамера, Гаусса, обратной матрицы:
ВАРИАНТ 5 Задание 1. Найти решение систем линейных уравнений методами Крамера, Гаусса, обратной матрицы:
Задание 2. Вычислить, выписать вещественную и мнимую части полученных комплексных чисел.
ВАРИАНТ 6 Задание 1. Найти решение систем линейных уравнений методами Крамера, Гаусса, обратной матрицы:
Задание 2. Вычислить, выписать вещественную и мнимую части полученных комплексных чисел.
ВАРИАНТ 7 Задание 1. Найти решение систем линейных уравнений методами Крамера, Гаусса, обратной матрицы:
Задание 2. Вычислить, выписать вещественную и мнимую части полученных комплексных чисел.
ВАРИАНТ 8 Задание 1. Найти решение систем линейных уравнений методами Крамера, Гаусса, обратной матрицы:
Задание 2. Вычислить, выписать вещественную и мнимую части полученных комплексных чисел.
ВАРИАНТ 9 Задание 1. Найти решение систем линейных уравнений методами Крамера, Гаусса, обратной матрицы:
Задание 2. Вычислить, выписать вещественную и мнимую части полученных комплексных чисел.
ВАРИАНТ 10 Задание 1. Найти решение систем линейных уравнений методами Крамера, Гаусса, обратной матрицы:
Задание 2. Вычислить, выписать вещественную и мнимую части полученных комплексных чисел.
Практическая работа №2. Предел функции. Вычисление производной функции. Исследование и построение графиков функций с помощью производной Цель работы. Сформировать навыки вычисления пределов последовательностей и пределов функций. Сформировать умение находить производные сложных функций, усвоить геометрический и физический смысл производной. Сформировать навыки нахождения неопределенных интегралов различными методами
В результате выполнения работы студенты осваивают следующие результаты обучения в соответствии с ФГОС СПО: умения: - решать прикладные задачи в области профессиональной деятельности; знания: -значение математики в профессиональной деятельности и при освоении профессиональной образовательной программы; -основные математические методы решения прикладных задач в области профессиональной деятельности; -основные понятия и методы математического анализа основы интегрального и дифференциального исчисления Порядок выполнения работы: 1. Повторите теоретические положения по теме и записать определение, формулы расчета и т.п. 2. Выполните задание, согласно своего варианта. Исходные данные возьмите в приложении. 3. Сделайте выводы по результатам работы
Теоретическая часть
Определение: Пусть функция f (x) определена в некоторой окрестности точки а, кроме, быть может, самой точки а. Число А называется пределом функции f (x) в точке а (или при х, стремящемся к а), если для любых значений аргумента (х ¹ а) изсколь угодно малой окрестности точки а, последовательность соответствующих значений функции f (x) мало чемотличается от А (т.е. f (x) приближенно равны А). В этом случае пишут Свойства пределов: Теорема 1: Функция не может иметь двух разных пределов в точке. Теорема 2: Предел суммы (разности) функций равен сумме (разности) их пределов, если последние существуют: Теорема 3: Предел произведения функций равен произведению их пределов, если последние существуют: Следствие: Постоянный множитель можно выносить за знак предела, т.е. Теорема 4: Предел отношений двух функций равен отношению их пределов, если последние существуют и предел делителя отличен от нуля: Правила дифференцирования
1) 2) 3) 4) 5)
Формулы дифференцирования
Графика функции Исследование функции целесообразно вести в определенной последовательности. 1. Найти область определения функции. 2. Найти (если это можно) точки пересечения графика с осями координат. 3. Найти интервалы знакопостоянства функции (промежутки, на которых 4. Выяснить, является ли функция четной, нечетной или общего вида. 5. Найти асимптоты графика функции. 6. Найти интервалы монотонности функции. 7. Найти экстремумы функции. 8. Найти интервалы выпуклости и точки перегиба графика функции.
Вариант 0. Задание 1. Раскрыть неопределённость
Решение. Здесь старшая степень переменной n равна 2. Поэтому почленно делим числитель и знаменатель на
Получаем ответ: предел данной функции при переменной, стремящейся к бесконечности, равен Задание 2. Исследовать функцию
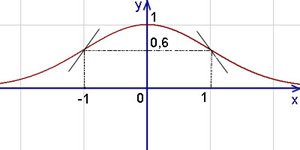
и построить её график. Решение. 1. Область определения функции – вся числовая прямая. Множеством значений данной функции, как и всякой показательной функции, служит интервал ]0, +∞[. Поэтому график функции расположен выше оси Ox, 2. Напомним: из школьного курса известно, что функция y = f (x) называется чётной, если
График чётной функции симметричен относительно оси Oy, так как, по определению, вместе с любой своей точкой (x; y) он содержит и точку (-x; y). Функция y = f (x) называется нечётной, если
График нечётной функции симметричен относительно начала координат, так как, по определению, вместе с любой своей точкой (x; y) он содержит и точку (-x; -y). Наша исследуемая функция чётная, так как
её график симметричен относительно оси Oy. Поэтому исследование можно выполнять только для ]0, +∞[. 3. Вертикальных асимптот у графика нет, поскольку функция непрерывна на всей числовой прямой. Горизонтальной асимптотой является ось Ox, так как
Поскольку кривая имеет двустороннюю горизонтальную асимптоту y = 0, у неё не может быть наклонных асиптот. 4. Находим Из уравнения Имеем Так как 5. Находим Из уравнения получаем
т.е. Учитывая чётность функции, исследуем знаки
Следовательно, при x = 1 кривая меняет выпуклость на вогнутость. Так как То точка перегиба кривой. Угловой коэффициент касательной в кривой в этой точке
поэтому в точке перегиба касательная образует с осью Ox тупой угол. 6. График не пересекает оси Ox, поскольку он расположен выше неё. Найдём точки пересечения кривой с осью Oy: полагая x = 0, имеем Тем самым получим точку (0; 1) графика, которая совпадает с точкой максимума. 7. Составим сводную таблицу исследования функции, куда внесём все характерные точки и интервалы между ними. Учитывая чётность функции, получаем следующую таблицу:
8. Используя результаты исследования, строим график функции
Требования к содержанию отчета по работе Отчёт о работе должен содержать название и цель работы, задание, результаты выполнения задания. По результатам работы необходимо сделать выводы.
Контрольные вопросы (Задания для самопроверки качества освоенных результатов обучения): - понятие предела функции в точке - понятие предела функции на бесконечности - основные теоремы о пределах - определение производной - геометрический и физический смысл производной - формулы производных суммы, произведения, частного функций - алгоритм исследования функции
Приложение Задание 1. Вычислить пределы последовательностей:
Задание 2
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 138; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.134.104.173 (0.294 с.) |
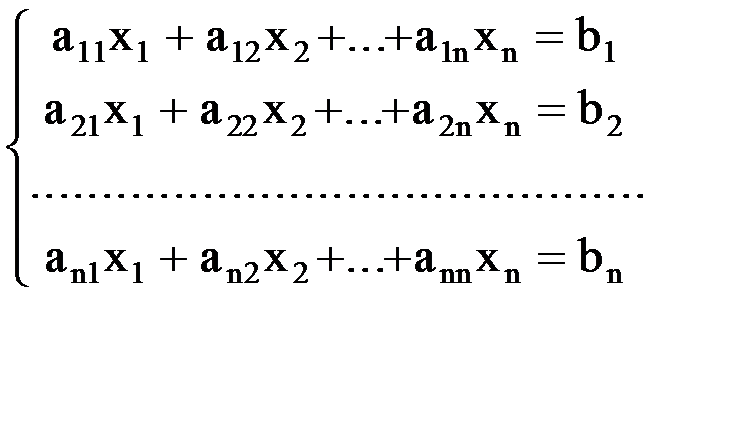 (1)
(1)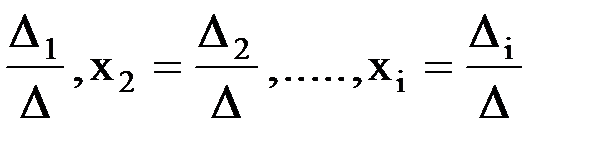 , где
, где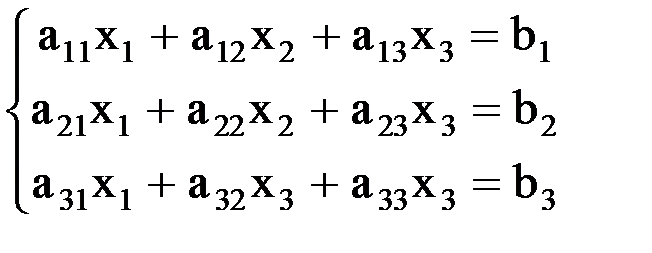 (2).
(2).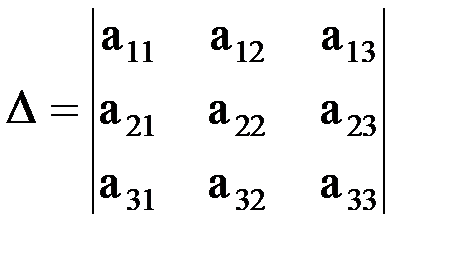 и вычислим.
и вычислим.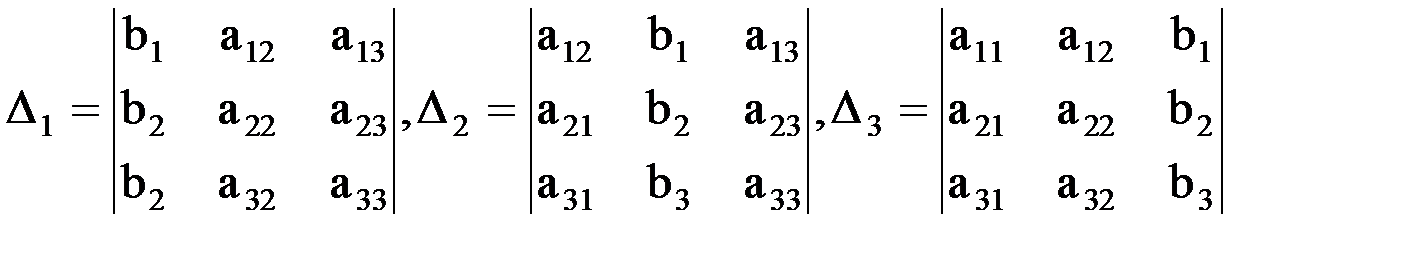 .
.
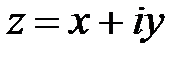 , (1.1)
, (1.1)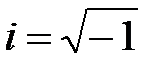 – мнимая единица. Первое из вещественных чисел, x, называется вещественной (действительной) частью комплексного числа (используется обозначение
– мнимая единица. Первое из вещественных чисел, x, называется вещественной (действительной) частью комплексного числа (используется обозначение 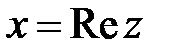 ); второе, y, - мнимой частью (
); второе, y, - мнимой частью (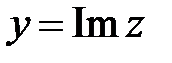 ). Выражение (1.1) называют алгебраической формой записи комплексного числа.
). Выражение (1.1) называют алгебраической формой записи комплексного числа.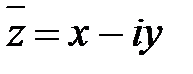 . Используя формулу разности квадратов, получаем, что
. Используя формулу разности квадратов, получаем, что 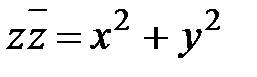 . Можно доказать, что корнями квадратного уравнения с отрицательным дискриминантом являются два сопряженных комплексных числа.
. Можно доказать, что корнями квадратного уравнения с отрицательным дискриминантом являются два сопряженных комплексных числа.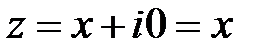 , а на оси OY – чисто мнимые числа
, а на оси OY – чисто мнимые числа 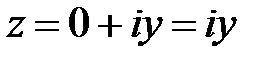 ).
).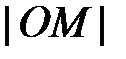 (или расстояние от начала координат до точки M), т.е.
(или расстояние от начала координат до точки M), т.е. 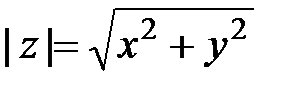 . Аргументом комплексного числа (
. Аргументом комплексного числа ( ) назовем угол, который вектор
) назовем угол, который вектор 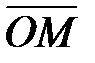 образует с положительным направлением оси OX. Главное значение аргумента, которое, как правило, используется при осуществлении действий с комплексными числами, удовлетворяет условию
образует с положительным направлением оси OX. Главное значение аргумента, которое, как правило, используется при осуществлении действий с комплексными числами, удовлетворяет условию 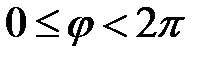 . При этом выражение вида
. При этом выражение вида (1.2)
(1.2)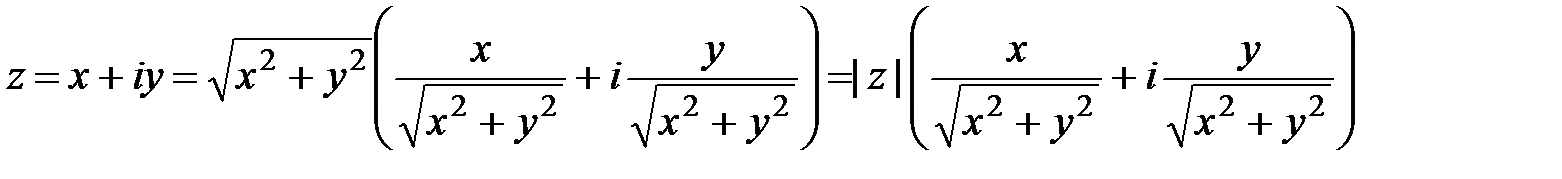
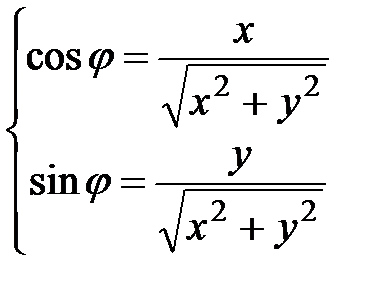 или
или 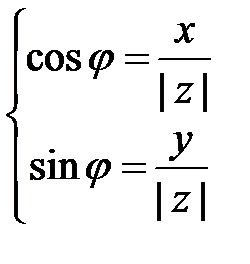 (1.3.)
(1.3.)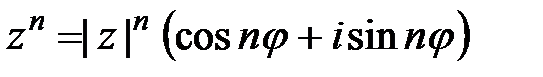 . (1.4)
. (1.4)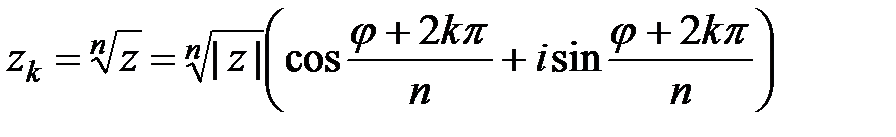 , k=0,1,…,n-1. (1.5)
, k=0,1,…,n-1. (1.5)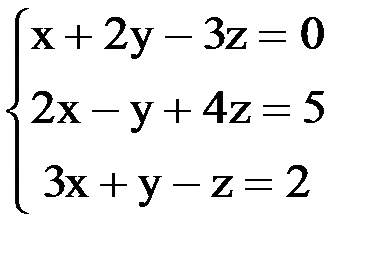
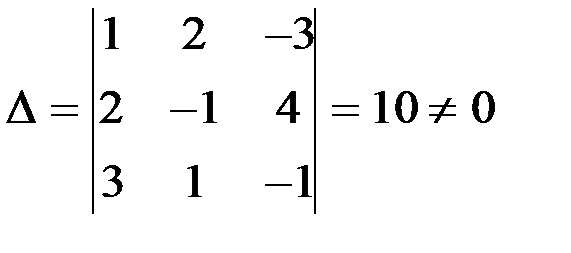
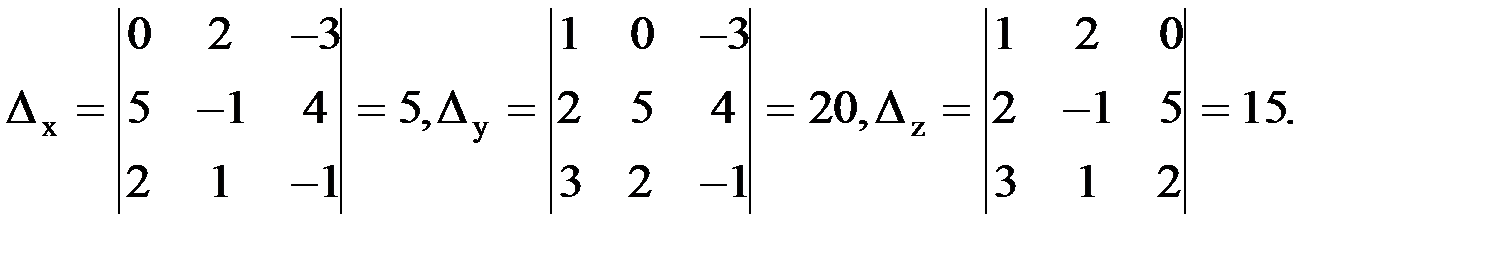
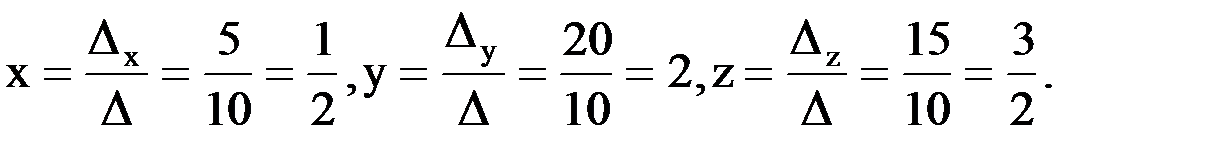
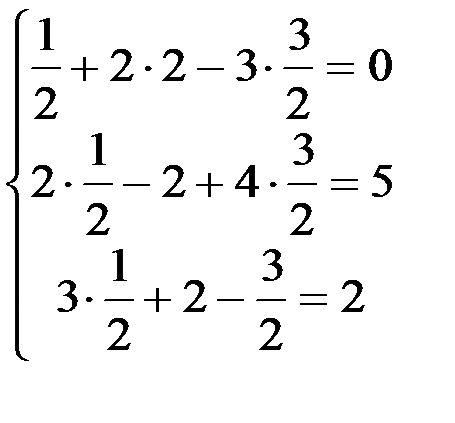 Ответ: x=0,5; y=2; z=1,5.
Ответ: x=0,5; y=2; z=1,5.
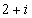 и
и 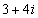 .
.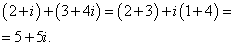
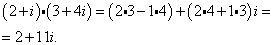
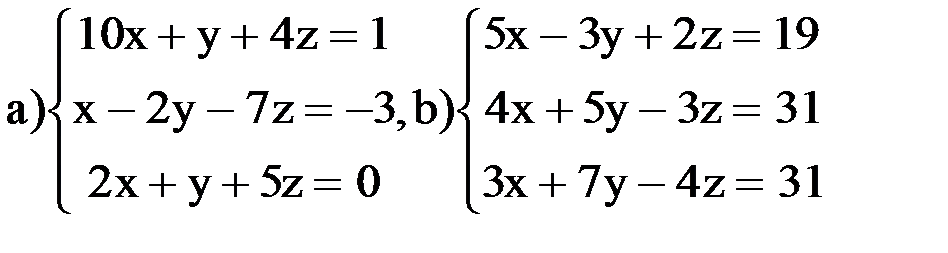

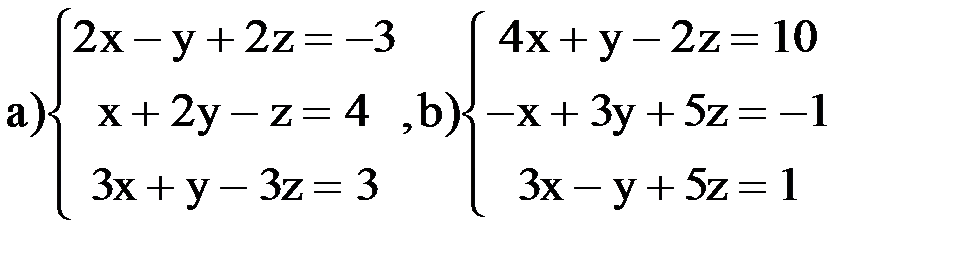
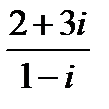
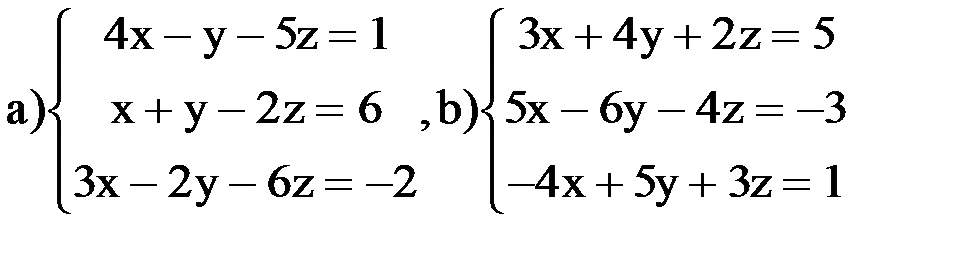
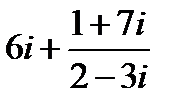
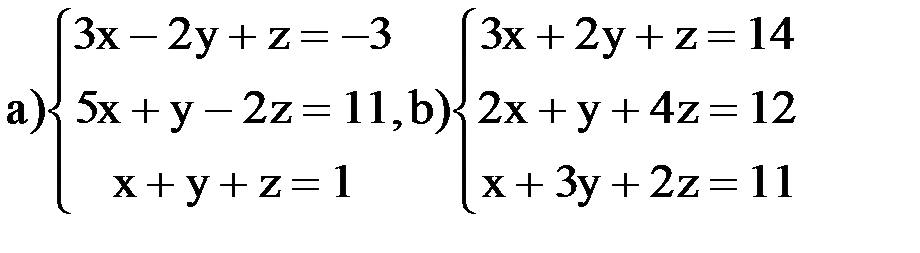
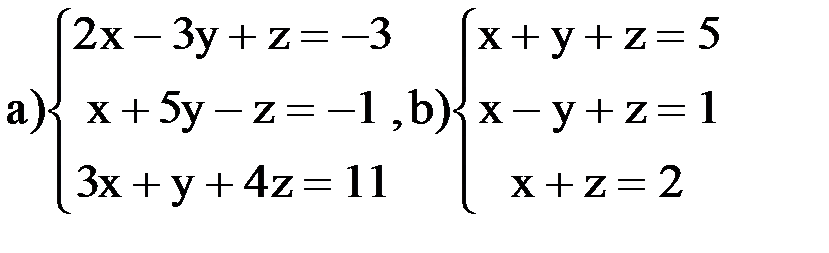
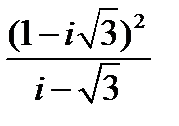
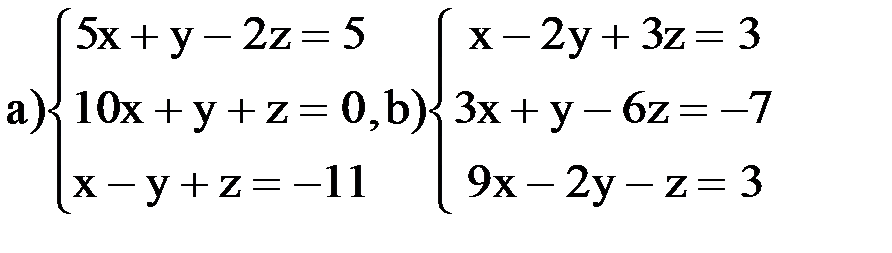
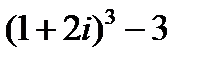
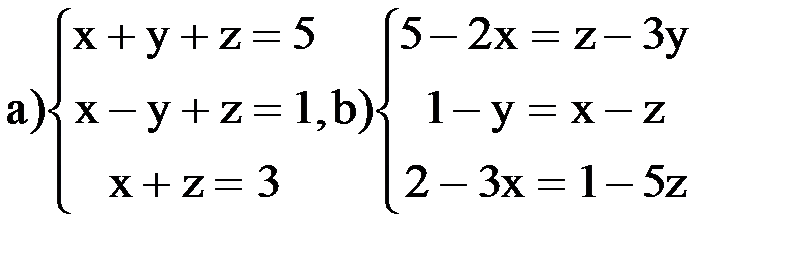
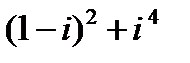
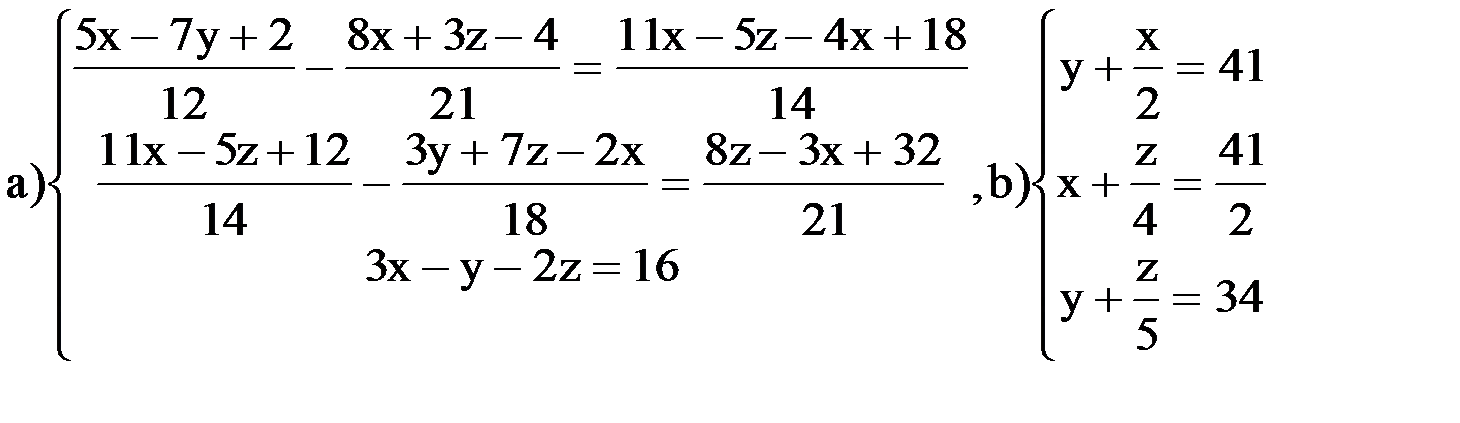
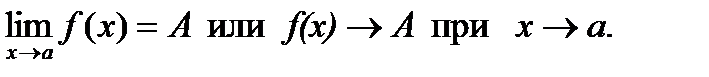
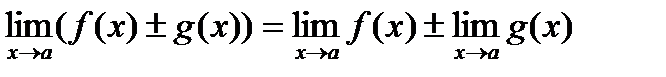 ,
,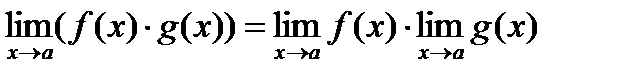 ,
, ,
,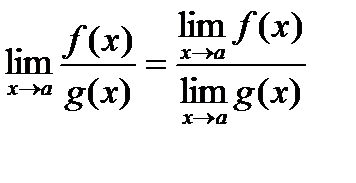 ,
,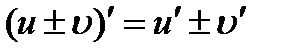 ;
;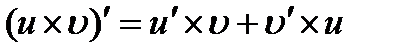 , в частности
, в частности 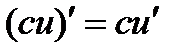 ;
;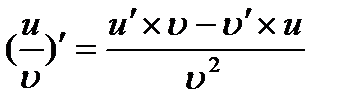 ;
;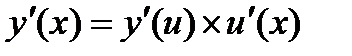 , если
, если 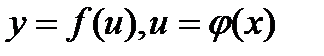 ;
;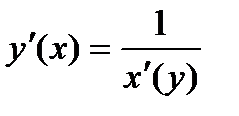 , если
, если 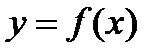 и
и 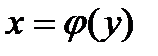 .
.
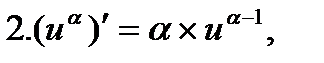 в частности,
в частности, 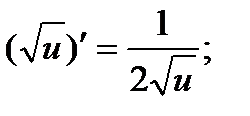
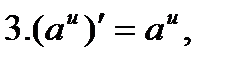 в частности,
в частности, 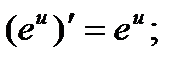
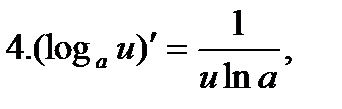 в частности,
в частности, 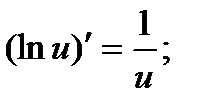
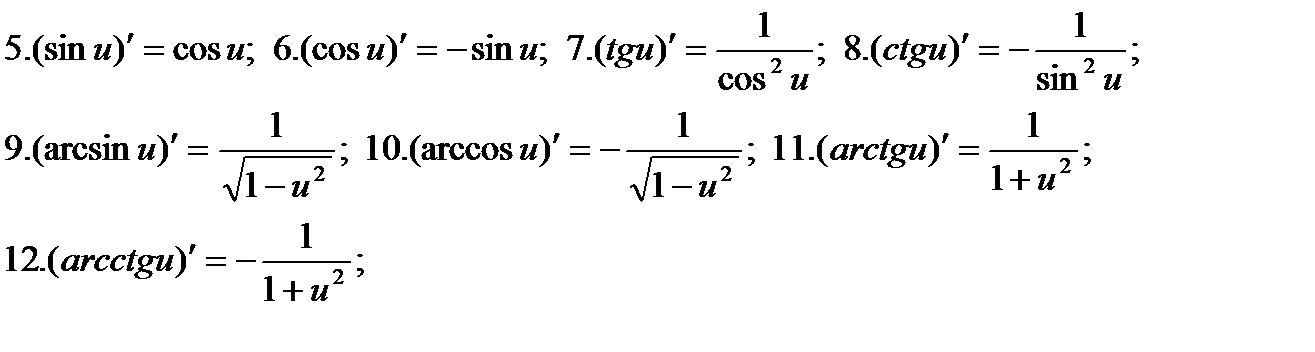
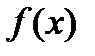 >0 или
>0 или 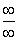 и найти предел
и найти предел 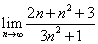 .
.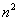 :
: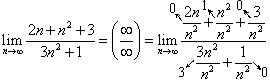 .
.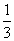 .
.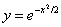
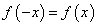 для всех x, принадлежащих области определения функции.
для всех x, принадлежащих области определения функции.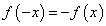 для всех x, принадлежащих области определения функции.
для всех x, принадлежащих области определения функции.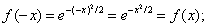
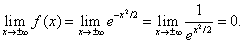
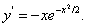
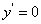
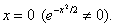
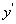 при переходе через значение x = 0 меняет знак с плюса на минус, то функция в точке x = 0 переходит от возрастания к убыванию, а (0; 1) – точка максимума. Касательная к кривой в этой точке горизонтальна, поскольку
при переходе через значение x = 0 меняет знак с плюса на минус, то функция в точке x = 0 переходит от возрастания к убыванию, а (0; 1) – точка максимума. Касательная к кривой в этой точке горизонтальна, поскольку 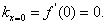
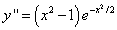
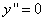
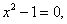
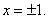
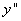 в окрестности только точки
в окрестности только точки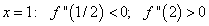
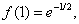
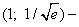
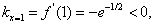
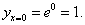
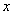
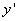
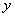
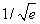
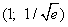 - точка перегиба, образует с осью Ox тупой угол
- точка перегиба, образует с осью Ox тупой угол