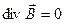Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема Гаусса и постулат Максвелла в дифференциальной форме.
Применим указанные законы для весьма малой поверхности S 0, ограничивающей объем D V с зарядом D q:
Для получения соотношений, связывающих заряды с векторами напряженности и смещения в некоторой точке внутри поверхности, необходимо перейти к пределу, устремив поверхность S 0 и объем D V к нулю, оставаясь в окрестности этой точки. Рассмотрим предел отношения обеих частей уравнений к объему D V, при D V стремящемся к нулю:
Предел отношения потока некоторого вектора сквозь поверхность S 0 к объему D V, ограниченному этой поверхностью при D V, стремящемся к нулю, называется расхождением или дивергенцией данного вектора в точке, в которую стягивается объем D V. Предел отношения заряда, находящегося в данном объеме, к величине D V, когда этот объем стремится к нулю, равен объемной плотности заряда в той же точке. Учитывая сказанное, запишем теорему Гаусса и постулат Максвелла в дифференциальной форме:
Термин «расхождение» легко понять, если вспомнить, что силовые линии векторов напряженности и смещения начинаются и заканчиваются на зарядах. В тех точках поля, где r = 0, Указанные соотношения в дифференциальной форме связывают характеристики электрического поля в любой точке. Они записаны в инвариантной форме и могут быть использованы в любой системе координат. Рассмотрим запись дивергенции вектора в декартовой системе координат. Для этого воспользуемся векторным дифференциальным оператором «набла» (
Так как дивергенция вектора является скалярной величиной, то ее можно представить в виде скалярного произведения оператора «набла» на соответствующий вектор, в результате такого умножения получаем сумму производных коллинеарных составляющих векторов:
Запишем по аналогии принцип непрерывности магнитного потока в дифференциальной форме:
Расхождение линий индукции в любой точке магнитного поля равно нулю, т.е. эти линии являются замкнутыми кривыми. Если будет открыт предсказанный теоретически Дираком магнитный заряд (монополь Дирака), то последнее уравнение изменится и в тех точках, где будет существовать магнитный заряд, в правой части уравнения вместо нуля появится плотность магнитного заряда, и это уравнение уже не будет называться принципом непрерывности.
|
|||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 51; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.125.139 (0.006 с.) |


 .
.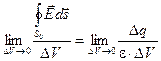 ;
; 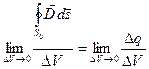 .
. ;
; 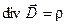 .
. и
и 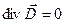 – расхождение линий из этих точек отсутствует. Линии из этих точек не расходятся и не сходятся к ним, а могут лишь проходить через эти точки.
– расхождение линий из этих точек отсутствует. Линии из этих точек не расходятся и не сходятся к ним, а могут лишь проходить через эти точки.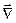 ), который записывается в виде суммы трех ортогональных составляющих:
), который записывается в виде суммы трех ортогональных составляющих: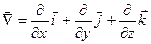
 .
.