Существует ли четвертое измерение?

В научно-фантастических произведениях иногда встречаются сюжеты (рис. 13 −  автор Эшер), в которых разумные существа осваивают четвертое, пятое и так далее измерения¹. Повышение размерности пространства предоставляет новые, богатейшие возможности как для этих существ, так и для писателей-фантастов. Сравните двухмерную плоскость и трехмерное пространство! Для того чтобы «выйти» из плоскости в трехмерное пространство, можно предложить следующий метод: из центра окружности необходимо провести бесконечный луч, который нигде не пересекает окружность − такой луч лежит в третьем измерении. По аналогии можно предложить «путь в четвертое измерение»: из центра сферы необходимо провести луч, который нигде не пересекает сферу. Вообразили? Еще один способ: провести прямую, которая перпендикулярна трем взаимно перпендикулярным прямым. Конечно, если вам не удалось представить себе такой луч или такую прямую, то это еще не является доказательством отсутствия четвертого измерения в нашем пространстве.

 

рис. 13

Попытаемся представить, к каким наблюдаемым явлениям могло бы привести наличие дополнительного измерения. Например, из четвертого измерения можно было бы заглянуть внутрь любого трехмерного тела (как из третьего измерения можно видеть «внутренности» любой плоской фигуры). Далее, был бы возможен бесследный «уход» и обратное появление в любом другом месте любых материальных тел (опять же представьте себе, что будет происходить на плоскости, которую пересекает трехмерное тело). К настоящему времени таких фактов не зафиксировано. Более того, не известны такие явления, которые не могли бы быть объяснены с точки зрения пространства трех измерений.

Еще одним доказательством трехмерности пространства, в котором мы обитаем, является ряд физических законов. Рассмотрим, например, точечный источник, который посылает свет во все стороны равномерно. Понятно, что энергия, пересекающая поверхность любой сферы, внутри которой находится источник, должна быть постоянна. Следовательно, интенсивность света (то есть энергия, приходящаяся на единицу площади) должна убывать обратно пропорционально площади сферы, то есть обратно пропорционально квадрату расстояния. Если бы свет распространялся и в четвертом измерении, то его интенсивность убывала бы обратно пропорционально кубу расстояния. Эксперимент однозначно утверждает, что интенсивность убывает обратно пропорционально квадрату расстояния. Эти и другие факты утверждают, что наше пространство действительно трехмерно.

Таким образом, ответ на вопрос этого раздела, в настоящее время следующий: пространство четырех и более измерений является математической абстракцией. Можно изучать свойства геометрических объектов в таких пространствах при решении целого ряда задач, в том числе физических, бывает полезно их рассматривать в многомерных пространствах. Однако в настоящее время нет никаких оснований полагать о реальном существовании четвертого измерения в том смысле, что реально существуют некоторые материальные тела вне пространства трех измерений.

Декарт Рене

Рене Декарт (фр. Ren? Descartes; лат. Renatus Cartesius − Картезий) − французский математик, философ, физик и физиолог, создатель аналитической геометрии и современной алгебраической символики, автор метода радикального сомнения в философии (рис. 14).

рис. 14

Декарт происходил из старинного, но обедневшего дворянского рода. Он родился 31 марта 1596 года в городе Лаэ во Франции. Его мать умерла, когда ему был один год. Воспитанием мальчика занималась бабушка по матери.

Начальное образование Декарт получил в иезуитском коллеже. Религиозное образование, как ни странно, только укрепило в молодом Декарте скептическое недоверие к тогдашним философским авторитетам. Позже он сформулировал свой метод познания − дедуктивные (математические) рассуждения над результатами воспроизводимых опытов.

В 1612 году Декарт закончил коллеж², некоторое время изучал право, затем уехал в Париж, где несколько лет чередовал рассеянную жизнь с математическими исследованиями. Затем в 1617 году он поступил на военную службу − сначала в революционную Голландию, затем в Германию, где участвовал в битве за Прагу во время тридцатилетней войны. Несколько лет Декарт провёл в Париже, предаваясь научной работе. Затем − ещё несколько лет участия в войне (осада Ларошели³). По возвращении во Францию оказалось, что свободомыслие Декарта стало известно иезуитам, и те обвинили его в ереси. Поэтому в 1628 году Декарт переехал в Голландию, где провёл 20 лет.

Он вёл обширную переписку с лучшими учёными Европы, изучал самые различные науки − от медицины до метеорологии. Наконец в 1634 году он закончил свою первую программную книгу под названием «Мир». Но момент для издания был неудачным − годом ранее инквизиция чуть не замучила Галилея. Теория Коперника, принятая и в книге Декарта, была официально запрещена. Поэтому Декарт решил при жизни не печатать этот труд.

Вскоре, однако, одна за другой появляются другие книги Декарта: «Рассуждение о методе...» (1637 г.); «Размышления о первой философии...» (1641 г.); «Начала философии» (1644 г.).

В «Началах философии» сформулированы главные идеи Декарта:

− бог сотворил мир и законы природы, а далее Вселенная действует как самостоятельный механизм;

− в мире нет ничего, кроме движущейся материи различных видов. Материя состоит из элементарных частиц, локальное взаимодействие которых и производит все природные явления;

− математика − мощный и универсальный метод познания природы, образец для других наук.

Кардинал Ришелье благожелательно отнёсся к трудам Декарта и разрешил их издание во Франции, а вот протестантские богословы Голландии наложили на них проклятие.

В 1649 году Декарт, измученный многолетней травлей за вольнодумство, поддался уговорам шведской королевы Кристины и переехал в Стокгольм. Почти сразу после переезда он серьёзно простудился и вскоре умер (11 февраля 1650 года). Предположительной причиной смерти явилась пневмония. Существует гипотеза об его отравлении, поскольку симптомы болезни очень сходны с симптомами при остром отравлении мышьяком.

К концу жизни Декарта отношение церкви к его учению стало резко враждебным. Вскоре после его смерти основные сочинения Декарта были внесены в «Индекс запрещенных книг», а Людовик XIV специальным указом запретил преподавание философии Декарта («картезианства») во всех учебных заведениях Франции.

Спустя 17 лет после смерти учёного его останки были перевезены в Париж (позже он был погребён в Пантеоне). В 1819 году многострадальный прах Декарта был вновь потревожен и ныне покоится в церкви
Сен-Жермен де Пре.

Научная деятельность Декарта очень разнообразна. В 1637 году вышел в свет главный математический труд Декарта − «Рассуждение о методе» (полное название − «Рассуждение о методе, позволяющем направлять свой разум и отыскивать истину в науках»). Символическую алгебру Декарт называл «Всеобщей математикой» и писал, что она должна объяснить «всё относящееся к порядку и мере».

Создание аналитической геометрии позволило перевести исследование геометрических свойств кривых и тел на алгебраический язык, то есть анализировать уравнение кривой в некоторой системе координат. Достоинства нового метода были исключительно велики, и Декарт продемонстрировал их в той же книге, открыв множество положений, неизвестных древним и современным ему математикам.

Вместе с конкретными научными открытиями было совершено ещё одно открытие. Обнаружилась необходимость и возможность постоянной работы над собственным умом, необходимость и возможность постоянного обращения мысли на мысль, постоянного развития самой способности мыслить, открывать, изобретать. Исходной точкой философских рассуждений Декарта является «сомнение во всем». Скептицизм был всегда выдающейся чертой французского ума, равно как и стремление к математической точности знаний.

Cogito, ergo sum (мыслю, следовательно существую) − есть первое и вернейшее из всех познаний, встречающееся каждому, кто философствует в порядке.

¹Для примера можно вспомнить знаменитый роман М. Булгакова «Мастер и Маргарита».

²А через год в России закончилась смута и на царский престол избран первый из Романовых − Михаил.

³Там он мог встречаться с «тремя мушкетерами» − Атосом, Портосом, Арамисом и Д'Артаньяном.

Материальная точка

Во многих кинематических задачах оказывается возможным пренебречь размерами самого тела. Еще раз рассмотрим автомобиль, движущийся из Минска в Брест. Расстояние между этими городами − порядка 350 километров, размеры автомобиля − несколько метров, поэтому в такой ситуации при описании положения автомобиля можно не учитывать его размеры (если капот автомобиля находится в Бресте у нужного подъезда нужного дома, то можно считать, что и его багажник находится приблизительно там же). Таким образом, в данной задаче можно мысленно заменить автомобиль его моделью − телом, размеры которого пренебрежимо малы. Такая модель тела очень часто используется в физике и называется материальной точкой.

Материальная точка − это идеальная модель тела, размерами которого в данных условиях можно пренебречь. Общим у геометрической и материальной точек является отсутствие собственных размеров. Материальную точку по мере необходимости можно «наделять» свойствами, которыми обладают реальные тела, например, массой, энергией, электрическим зарядом и так далее.

Одним из критериев применимости модели материальной точки является малость его размеров по сравнению с расстоянием, на которое перемещается тело. Однако это условие не является абсолютно однозначным. Так, описывая движение Земли вокруг Солнца при расчете ее положения на орбите, размерами Земли можно пренебречь, считая ее материальной точкой (рис. 15 − Николай Коперник и его гелиоцентрическая модель Солнечной системы.).

 

рис. 15

 

Однако если нам необходимо рассчитать времена  восхода и заката Солнца, модель материальной точки принципиально неприменима, так как это описание требует учета вращения Земли, ее размеров и формы (рис. 16. Восход Земли − вид с Луны).

 

 

рис. 16

 

Рассмотрим еще один пример. Спринтеры соревнуются на стометровой дистанции. Цель описания движения − выявить, кто из спортсменов пробегает дистанцию за меньшее время (то есть задача чисто кинематическая). Можно ли в данной задаче считать бегуна материальной точкой? Его размеры значительно меньше дистанции забега, но достаточно ли они малы, чтобы ими можно было пренебречь? Ответ на эти вопросы зависит от требуемой точности описания. Так, на серьезных соревнованиях время измеряется с точностью 0,01 секунды. За это время бегун смещается на расстояние порядка 10 сантиметров (простая оценка, полученная исходя из средней скорости спринтера 10 м/с). Следовательно, погрешность, с которой определяется положение бегуна (10 см), меньше, чем его поперечные размеры, поэтому модель материальной точки в данном случае неприменима. Не случайно мастера спринтерского бега на финише «бросают грудь вперед», выигрывая драгоценные сотые доли секунды (рис. 17. Есть мировой рекорд! У. Болд).

 

 

рис. 17

Упражнение.

Оцените, можно ли  использовать модель материальной точки, если время забега измеряется с точностью 0,1 с.

В некоторых ситуациях можно использовать модель материальной точки, даже если размеры тела сравнимы и больше расстояний, на которое смещается тело. Это допустимо тогда, когда положение одной точки тела однозначно определяет положение всего тела. Так, при скольжении бруска по наклонной плоскости можно найти положение всего тела, зная положение его центра (как, впрочем, и любой другой точки).

Если модель материальной точки оказывается неприменимой, то необходимо использовать другие, более сложные модели.

Абсолютно твердое тело

Многие реальные тела являются твердыми, то есть в течение длительного  времени сохраняют свои размеры и форму, точнее говоря, изменения размеров и формы настолько незначительны, что ими можно пренебречь. Моделью таких тел служит абсолютно твердое тело.

Абсолютно твердое тело − это идеальная модель тела, изменением размеров и формы которого в данных условиях можно пренебречь.

Из этого определения следует, что расстояние между двумя любыми точками абсолютно твердого тела остается неизменным. Абсолютно твердое тело можно также рассматривать как совокупность материальных точек, жестко связанных между собой. Так, положение океанского лайнера в открытом море можно описать, пользуясь моделью материальной точки, а его пространственную ориентацию (курс, наклон) − с помощью модели абсолютно твердого тела (рис. 18).

 

рис. 18

 

Применимость модели абсолютно твердого тела обусловлена только конкретной исследуемой проблемой − целью моделирования и требуемой точностью.

В заключение отметим, что рассмотренные нами модели не исчерпывают всех типов моделей тел, используемых в физике. Например, того же бегуна нельзя описать и в рамках модели абсолютно твердого тела, так как здесь важно взаимное расположение частей тела − туловища, рук, ног, головы и изменение этого положения. В таких ситуациях можно использовать модель, состоящую из нескольких движущихся друг относительно друга твердых тел и материальных точек (рис. 19).

 

 

рис. 19

Число степеней свободы тела

Теперь после того, как мы изучили несколько моделей тел, можно окончательно и корректно сформулировать ответ на вопрос о том, что значит задать, определить положение тела: указать численное значение координат некоторых точек тела так, чтобы положение всего тела (любой его части) было определено однозначно.

Число независимых координат, которые однозначно определяют положение тела или системы тел в пространстве, называется числом степеней свободы.

Число степеней свободы − очень важная характеристика описываемой системы хотя бы потому, что определяет число независимых уравнений, описывающих движение системы.

Подсчитаем число степеней свободы некоторых простых систем.

Материальная точка, по определению, не имеет размеров, поэтому ее положение в пространстве определяется однозначно тремя координатами. Следовательно, число степеней свободы свободно материальной точки равно трем.

Если на движение материальной точки накладываются дополнительные условия, то число ее степеней свободы может уменьшиться. Так, если точка движется по заданной поверхности, то ее положение определяется двумя независимыми координатами. Следовательно, число степеней свободы равно двум; при движении по заданной линии число степеней свободы уменьшается до одной. Подчеркнем, это не значит, что при движении по заданной линии может изменяться только одна − и могут изменяться все три, но положение точки на заданной линии определяется одной координатой, и если она известна, то могут быть определены и две другие. Тем не менее описание положения точки на заданной линии с помощью одной координаты оказывается не всегда удобным. Ценность рассмотренных нами декартовых координат в том, что они позволяют установить физические законы, описывающие движение вдоль всех прямых (все прямые одинаковы!). В то же время для описания изменения координат на произвольной линии пришлось бы записывать свои законы для каждой линии − окружности, параболы, синусоиды и т. д. Поэтому часто одномерное движение вдоль известной линии описывают с помощью двух или трех координат. Однако и в этом случае число степеней свободы остается равным единице.

Если механическая система может быть промоделирована как совокупность материальных точек, движущихся в пространстве, то очевидно, что полное число ее степеней свободы равняется – 3N. Но если на движение этих материальных точек накладываются дополнительные ограничения, то число степеней свободы уменьшается.

Рассмотрим, как можно описать положение в пространстве двух материальных точек, жестко связанных между собой (что-то похожее на гантели) (рис. 20).

 

рис. 20

Две точки имеют шесть степеней свободы, которые могут быть описаны шестью координатами − х₁, у₁, z₁, х₂, y₂, z₂, но так как расстояние между точками неизменно, то на эти координаты накладывается условие:

 

(x₁ − x₂)² + (y₁ − y₂)² + (z₁ − z₂)² = l²,

 

где l − расстояние между точками. Поэтому число независимых координат, или число степеней свободы, равно пяти.

Таким  образом, число степеней свободы системы, состоящей из N материальных точек, равно 3N минус число дополнительных условий (связей), накладываемых на движение этих точек.

Число степеней свободы может быть подсчитано и другим способом. Обратим внимание, что точное определение координат уменьшает «подвижность» точки (или системы точек). Так, например, если для материальной точки задана координата z, то точка может двигаться только в плоскости, перпендикулярной оси Z, а задание еще одной координаты (скажем y) приводит к тому, что точка может двигаться только вдоль прямой, параллельной оси X. Поэтому число степеней свободы можно находить, подсчитывая, сколько независимых координат необходимо определить, чтобы жестко «закрепить» тело.

С помощью такого подхода найдем число степеней свободы системы, состоящей из двух жестко связанных точек. Задавая три координаты одной точки, мы ее мысленно закрепляем (рис. 21).

 

 

рис. 21

 

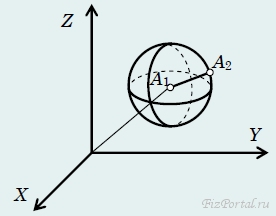
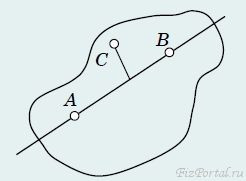
Тогда вторая точка может двигаться только так, чтобы ее расстояние до первой оставалось неизменным, то есть по поверхности сферы радиуса l. Понятно, что если определено положение двух точек твердого тонкого стержня, то задано и положение всего стержня, поэтому тонкий стержень имеет пять степеней свободы.

Посчитаем число степеней свободы свободно движущегося абсолютно твердого тела. Выберем внутри тела три произвольные точки А, В, С, не лежащие на одной прямой (рис. 22).

 

рис. 22

 

Положение одной точки А определяется тремя координатами; если задано положение точки А, то положение точки В может быть описано двумя координатами. Наконец, при «закрепленных» точках А и B тело может только вращаться вокруг оси, проходящей через эти точки. Следовательно, точка С имеет одну степень свободы. Таким образом, абсолютно твердое тело имеет шесть степеней свободы.

Как мы уже отмечали, для описания положения точки можно использовать разные системы координат, аналогично, положение твердого тела также может быть описано различными способами, только число независимых координат во всех способах описания будет одним и тем же, равным числу степеней свободы. Так, во многих случаях положение твердого тела описывают, задавая три декартовые координаты одной из его точек (чаще центра) и три угла, определяющие его ориентацию.

Эти углы можно задавать по-разному. Но наиболее популярной является система углов Л. Эйлера. Интересно, что специалисты разных областей используют фактически одну и ту же систему, но называют эти углы по своему. Так физики обычно рассматривают движение волчка (рис. 23) − хорошо знакомой с раннего детства юлы. Ее движение можно представить в таком виде:

 

 

рис. 23

 

1) быстрое вращение вокруг собственной оси (собственное вращение);

2) медленный поворот оси юлы вокруг вертикали, при этом ось юлы описывает конус − такое движение называют прецессией;

3) колебания оси юлы, то есть изменение угла между осью юлы и вертикалью − это движение называют нутацией.

Соответственно, углы, задающие положение твердого тела, называются углами прецессии, нутации и собственного вращения.

Если внимательно присмотреться к этим углам, то в углах прецессии и нутации можно узнать географическую широту и долготу.

Специалисты по динамике движения самолетов (рис. 24)

 

 

рис. 24

 

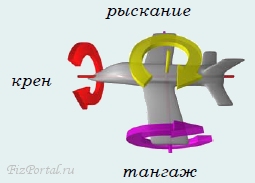
также используют три угла для задания его ориентации, но названия углов у них иные − крен, тангаж, рыскание (рис. 25):

 

 

рис. 25

 

− крен (от фр. car?ne − киль, подводная часть корабля или от англ. kren-gen − класть судно на бок) − поворот самолёта вокруг его продольной оси;

− тангаж (фр. tangage − килевая качка), поворот или раскачивание самолета вокруг поперечной горизонтальной оси (когда нос опускается вниз − пикирование или поднимается вверх − кабрирование);

− рыскание (рысканье) − угловое вращение или раскачивание самолёта вокруг вертикальной оси на небольшой угол, а также небольшие изменения курса вправо или влево.

У моряков своя терминология (для тех же углов): тангаж заменен на дифферент, рыскание на курс, но крен остался креном.

В заключение раздела посчитаем число степеней свободы, которым обладает  человеческая рука: 2 − в плечевом суставе; 2 − в локтевом, 2 − в кистевом; 4 − в каждом пальце. Итого − 26 степеней свободы. 26 чисел необходимо задать, чтобы описать положение одной человеческой руки! (Рис. 26).

 

рис. 26