Координаты точки на плоскости

Механика.

 

Часть I. Кинематика

 1. Математическое описание положения тела

В повседневной жизни нам довольно часто приходится указывать положение того или иного предмета, и мы без особых трудностей справляемся с этой задачей. Так, например, на вопрос «Где находится Белгосуниверситет?» можно дать ответ: «Белгосуниверситет находится в городе Минске».

 

Признать этот ответ удовлетворительным во всех случаях невозможно. Так, если спрашивающий инопланетянин не знает, что Минск − столица Республики Беларусь, государства, расположенного в восточной Европе, то данный ответ для него не несет никакой новой информации. С другой стороны, если спрашивающий − абитуриент, приехавший на вокзал города Минска, то ваш ответ для него ясен, но явно недостаточен. Указание местоположения, во-первых, должно быть однозначно понято и, во-вторых, должно обеспечивать необходимую точность описания. Словесный способ описания положения распространен очень широко: это названия планет, материков, стран, городов, улиц и так далее. Однако, несмотря на повсеместное использование такого описания и его поэтичность, оно имеет ряд существенных недостатков:

− невозможно дать персональное «имя» каждой точке пространства;

− уточнение положения требует существенного усложнения описания;

− словесное описание, как правило, ничего не говорит о взаимном расположении описываемых мест.

Эти недостатки можно частично преодолеть, используя численное описание положения тела. В отличие от количества слов, количество чисел не ограничено; уточнение положения достигается заданием чисел с большей точностью; числовое описание упорядочивает места в пространстве, позволяет говорить об их взаимном расположении.

Впрочем, с числовым описанием положения вы также сталкивались в обычных жизненных ситуациях − это нумерация домов, квартир, мест в кинотеатре, страниц книги и тому подобное. Математический способ описания точек пространства (или, что равносильно, положения тел в пространстве) указывает их числовой «адрес» − каждой точке пространства ставится во взаимно однозначное соответствие некоторый набор чисел. Эти числа, которые однозначно определяют положение точки, называются ее координатами.

Координаты точки на прямой

Очевидно, что не всегда от нас требуется задавать «адреса» всех точек  пространства. Если мы хотим описать движение тела вдоль заданной линии (например, автомобиля, движущегося по магистрали Минск − Брест), то достаточно указать способ задания координат на этой линии.
Для простоты будем считать,  что такой линией является прямая. Наша задача − каждой точке этой прямой поставить во взаимно однозначное соответствие некоторое число − координату точки.
Выберем на данной прямой некоторую точку О (рис.),

 

рис. 1

которую назовем началом отсчета. Подчеркнем, что и сама прямая, и начало отсчета должны быть изначально заданы, то есть известны всем, для кого предназначено наше описание. С точки зрения геометрии, все точки на прямой равноправны, поэтому выбор начала отсчета произволен, с точки здравого смысла, предпочтительнее выбрать точку начала отсчета так, чтобы она чем-то отличалась, была хорошо известна. Например, если выбранная прямая «описывает» дорогу, то начало отсчета следует выбирать в крупном населенном пункте, хорошо всем известном. Но, как мы увидим в дальнейшем, и с физической точки зрения выбор начала отсчета также произволен.

Действительно, выбор точки начала отсчета определяется произвольно, но эта  точка, во-первых, должна быть однозначно определена, во-вторых, достаточно известна. Как, например, в нашей республике задан «нулевой километр» (рис.)?

 

рис. 2

 

В прежние годы нулевой километр отсчитывался от главпочтамта. Новый знак оказался ровно на 1 км в стороне от него.

В самом центре Минска, на юго-восточной кромке Октябрьской площади, размещен этот «Гринвичский меридиан» Беларуси. Его еще называют «нулевой километр».

Гранитный камень в форме пирамиды, символизирующий вечность и прочность, вытесан в солнечной Португалии. Обрамляют знак бронзовые картуши, на которых размещены карта дорог, латинское изречение, стихи, написанные Я. Коласом. На бронзовой отмостке «нулевого километра» указаны расстояния от Минска до столиц соседних государств, областных и районных центров Беларуси.

Авторы знака − архитектор А. Сардаров, скульптор А. Финский, художник по металлу В. Заведеев.

После того, как начало отсчета задано, положение любой другой точки А на прямой может быть охарактеризовано расстоянием l от этой точки до начала отсчета. Однако только расстояние не определяет положение точки однозначно − необходимо указать, с какой стороны от начала отсчета находится точка А. Конечно, это можно сделать и словесно: справа − слева, восточнее − западнее... Но гораздо проще и удобней договориться обозначать направление с помощью знаков − в одну сторону «плюс», в другую «минус». Иными словами, точке А, находящейся на расстоянии l от начала отсчета с одной стороны, приписывается координата х = l, а точке А^/, находящейся на расстоянии l с другой стороны, присваивается координата х = l (рис. 1). Удобства такого соглашения очевидны: такое описание остается числовым (хотя числа могут быть как положительными, так и отрицательными), над этими числами можно проводить математические операции, результаты которых будут иметь определенный физический смысл. Таким образом, прямая становится направленной (т.е. осью координат), причем выбор положительного направления столь же произволен, как и выбор начала отсчета. Для того чтобы каждой точке оси можно было поставить в соответствие число (оцифровать ось), необходимо также указать единицу измерения расстояний, так как только при заданной единице измерения физическая величина приобретает однозначный смысл.

Заметьте, что построенная нами оцифрованная направленная прямая с заданной точкой отсчета является фактически числовой осью (с которой вы познакомились в курсе математики). Однако в физическом описании числа этой оси (координаты точки) имеют строгий смысл: декартовой координатой точки на прямой является число, модуль которого равен расстоянию до начала отсчета, а знак указывает, с какой стороны от начала отсчета находится данная точка. Так как координата точки указывает расстояние до начала отсчета, то ее размерность − размерность длины (в СИ такой единицей измерения является метр). Метр был впервые введён во Франции в XVIII веке и имел первоначально два конкурирующих определения:

– как длина маятника с полупериодом качания на широте  45°, равным 1 с (в современных единицах эта длина равна примерно 0,981 м);

– как одна сорокамиллионная часть Парижского меридиана (то есть одна десятимиллионная часть расстояния от северного полюса до экватора по поверхности земного эллипсоида на долготе Парижа). Первоначально за основу было принято первое определение (8 мая 1790 года, Французское Национальное собрание). Однако, поскольку ускорение свободного падения зависит от широты и, следовательно, маятниковый эталон недостаточно воспроизводим, Французская академия наук в 1791 году предложила Национальному собранию определить метр через длину меридиана. 30 марта 1791 года это предложение было принято. 7 апреля 1795 года Национальный Конвент принял закон о введении метрической системы во Франции и поручил комиссарам, в число которых входили Ш. О. Кулон, Ж. Л. Лагранж, А. Л. Лавуазье, П. С. Лаплас и другие учёные, выполнить работы по экспериментальному определению единиц длины и массы. Первый прототип эталона метра был изготовлен из латуни в 1795 году. Следует отметить, что единица массы (килограмм, определение которого было основано на массе 1 дм³ воды), тоже была привязана к определению метра. В 1799 году из сплава 90 % платины и 10 % иридия был изготовлен эталон метра, длина которого соответствовала одной сорокамиллионной части Парижского меридиана. Впоследствии, однако, выяснилось, что из-за неправильного учёта полюсного сжатия Земли эталон оказался короче на 0,2 мм; таким образом, длина меридиана лишь приблизительно равна 40 000 км.
Во время правления Наполеона  метрическая система распространилась по всей Европе. В 1917 году она была введена в России. Только в Великобритании, которая не была завоёвана Наполеоном, остались традиционные меры длины: дюйм, фут и ярд.
В 1889 году был  изготовлен более точный международный эталон метра − тоже из сплава платины и иридия − и имеет поперечное сечение в виде буквы «X» (рис. 3).

 

рис. 3

Его копии были переданы на хранение в страны, в которых метр был признан в качестве стандартной единицы длины. Этот эталон всё ещё хранится в Международном бюро мер и весов, хотя больше по своему первоначальному назначению не используется.

С 1960 года было решено отказаться от использования изготовленного людьми предмета в качестве эталона метра, и с этого времени по 1983 год метр определялся как число 1 650 763,73, умноженное на длину волны оранжевой линии (6056 А) спектра, излучаемого изотопом криптона-86 в вакууме.
Современное определение метра в  терминах времени и скорости света было введено в 1983 году: метр − это длина пути, проходимого светом в вакууме за 1/299 792 458 секунды.
Из этого  определения следует, что в СИ скорость света в вакууме принята равной в точности 299 792 458 м/с. Таким образом, определение метра, как и два столетия назад, вновь привязано к секунде, но на этот раз с помощью универсальной мировой константы − скорости света.
Заметим, что можно ввести координату точки на  произвольной заданной линии, измеряя длину участка этой линии между данной точкой и началом отсчета и указывая с помощью знаков, с какой стороны от начала отсчета находится точка. Километровые столбы на дорогах могут служить прекрасной иллюстрацией таких координатных отметок.
Таким образом, положение точки на  любой линии однозначно определяется одним числом. Поэтому говорят, что линия имеет одно измерение, а движение тела вдоль заданной линии называется одномерным.

Относительность координат

Итак, мы добились поставленной цели: дали «имя», указали «точный адрес» произвольной точке пространства − каждой точке пространства поставили в однозначное соответствие набор чисел − координат. Однако знание только этих чисел не дает возможности указать конкретную точку. Эти числа-координаты имеют смысл только тогда, когда указана (известна) система отсчета − начало отсчета, направление осей и единица измерения расстояний. Только в этом случае координаты указывают на конкретную точку пространства. Если изменить систему отсчета (начало отсчета, направление осей) или единицу измерения, то изменятся и координаты всех точек. Иными словами, координаты всех точек относительны, заданы относительно оговоренной системы координат. Выбор системы координат, как мы неоднократно подчеркивали, совершенно произволен. Существенна ли эта неопределенность в выборе системы координат? Нужно ли вообще говорить о координатах, если каждый имеет полное право ввести свою собственную систему координат? Мы вынуждены примириться с этим произволом и бояться его не надо, потому что:

− иного способа математического описания положения точки в пространстве не существует;

− всегда можно в каждом конкретном случае договориться о выборе системы отсчета, тем более что часто наиболее удачный выбор системы отсчета очевиден и определяется описываемой ситуацией. Например: расположение мебели в конкретной комнате не слишком удобно проводить в системе отсчета, связанной с почтамтом, скорее всего, каждый расположит начало отсчета в одном из углов комнаты и направит оси координат вдоль «ребер» комнаты;

− произвол в выборе системы отсчета дает нам определенную свободу, дает право воспользоваться возможностью выбора в своих интересах так, чтобы в каждом конкретном случае упростить описание физического явления;

− всегда можно (и следует) найти такие физические величины, которые не зависят от выбора системы координат. Например – расстояния между точками, углы между прямыми, площади фигур;

– всегда возможно установить формулы преобразования координат при переходе из одной системы отсчета в другую.

Как видим (и в этом мы сможем убедиться неоднократно в дальнейшем), физика − наука демократичная, она предоставляет каждому «свободу выбора», только надо уметь, и не бояться, ею пользоваться. В физике существует множество законов, но «все, что не запрещено, разрешено», различные точки зрения допустимы, но вполне примиримы друг с другом либо путем компромисса, либо путем установления общих «правил игры».

Наконец, следует помнить, что в физике существуют некие «абсолютные ценности», не зависящие от выбранной точки зрения.

1.5. Преобразования координат

Рассмотрим, как будут изменяться координаты точек при различных преобразованиях системы отсчета. Первый пример − изменение единицы измерения длины при неизменных начале отсчета и направлениях осей координат. Так как координаты точки представляют собой расстояния от проекций точки на оси координат до начала отсчета, то при изменении единицы измерения длины координаты будут изменяться так же, как изменяется численное значение длин и расстояний, то есть умножаться на коэффициент, связывающий различные единицы измерения. При изменении направления оси очевидно, что соответствующие координаты изменят знак на противоположный.

Получим теперь формулы преобразования координат при  сдвиге начала отсчета. Пусть на плоскости введены две системы декартовых координат ХОY и Х^/О^/Y^/, оси которых попарно параллельны (рис. 7)

 

рис. 7

Обозначим координаты точки О^/ в системе отсчета ХОY через х_o и у_o. Пусть координаты произвольной точки А в системе отсчета Х^/О^/Y^/ равны х^/ и у^/. Тогда, как следует из рисунка, координаты х, у этой же точки в системе отсчета ХОУ могут быть найдены по формулам

x₁ = x_o + x^/; y₁ = y_o + y^/. (1)

 

Легко записать формулы  обратного перехода от координат в системе отсчета ХОY к координатам в системе отсчета Х^/О^/Y^/:

x^/ = −x_o + x; y^/ = −y_o + y. (2)

 

Как и следовало ожидать, формулы обратного  преобразования (2) полностью аналогичны формулам (1), так как −х_o и −у_o есть координаты точки О в системе отсчета Х^/О^/Y^/. Эти формулы называют преобразованиями сдвига. Назовем систему отсчета ХОY исходной, а систему отсчета Х^/О^/Y^/ смещенной. (Очевидно, что эти названия условны, так как две рассматриваемые системы равноправны, и их можно поменять местами.)

Тогда правила преобразований сдвига можно сформулировать следующим образом: при смещении начала координат координаты всех точек уменьшаются на величину соответствующего смещения начала отсчета; координата точки в смещенной системе координат равна координате в исходной системе минус соответствующая координата начала отсчета смещенной системы.

  Упражнение.
Получите формулы преобразования сдвига для  одномерного и трехмерного случаев.

Существенным является тот факт, что в любом случае, при любом изменении  системы отсчета можно найти формулы преобразования координат. Следовательно, если положение тела описано в одной системе отсчета, то оно описано и в любой другой.

Упражнение

Покажите, что расстояние между двумя точками в пространстве вычисляется по формуле

s = √{(x₂ − x₁)² + (y₂ − y₁)² + (z₂ − z₁)²}.

Давайте теперь попытаемся вычислить расстояние между этими же точками, но в другой системе отсчета Х^/О^/Y^/, которая сдвинута относительно исходной системы координат ХОY. В этой системе отсчета координаты точек А₁ и А₂ можно найти по формулам преобразований (1)

x₁^/ = −x_o + x₁; x₂^/ = −x_o + x₂. (5)\

 

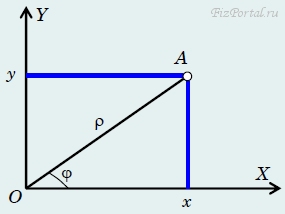
Как следует из этих формул, х₂ − х₁ = х₂^/ − х₁^/,

что, впрочем, и должно быть: если вторая точка лежит правее первой, то это их взаимное расположение не зависит от выбора системы координат, расстояние между проекциями точек на одну и ту же ось не зависит от начала отсчета. Аналогичное соотношение можно записать и для координат у этих точек, поэтому, как следует из здравого смысла, результат вычисления по формуле (4) не зависит от выбора системы координат (конечно, при неизменной единице измерения длины). Мы показали это для преобразования сдвига, однако очевидно, что и при повороте системы координат формула (4) должна давать один и тот же результат. Весьма интересная ситуация: все четыре координаты при изменении системы отсчета изменяются, а величина расстояния остается неизменной!

Величины, которые остаются неизменными при изменении системы координат, называются инвариантными.

Вот еще одно подтверждение возможности использования систем координат − можно найти физические величины, которые не зависят от выбора системы координат. Поиск таких инвариантных физических величин очень важен, потому что, как правило, именно они проще всего поддаются измерению, именно они фактически определяют протекание того или иного физического процесса, именно они убеждают скептиков в возможностях правильного физического описания различных явлений.

Полярная система координат

Декартовая система координат на плоскости является, безусловно, самой простой, однако не единственно возможной. Во многих случаях предпочтительнее использовать другие криволинейные системы координат. Среди этих координат наиболее часто используется полярная система (рис. 9).

 

рис. 9

 

Положение точки А на плоскости в этом случае описывается координатами: величинами ρ − полярное расстояние (ОА) и φ − полярный угол (АОх). Очевидно, что координата ρ неотрицательна, угол φ может принимать любые значения. Легко выразить декартовые координаты точки через полярные:

 

x = ρcosφ; y = ρsinφ. (1)

 

Обратное преобразование несколько сложнее:

ρ = √{x² + y²}; φ = arctg(y/x) ± kπ. (2)

 

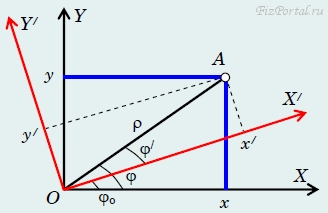
Заметим, что полярный угол определяется неоднозначно, при добавлении к нему любого кратного 2π положение точки на плоскости не изменяется. Эта неоднозначность редко приводит к недоразумениям, зато оговоренное произвольное (от минус до плюс бесконечности) изменение угла позволяет легко и красиво описывать некоторые виды механического движения тел (например, вращение).

Получим теперь формулы преобразования координат точки при повороте системы координат. Рассмотрим две декартовые системы координат ХОY и Х^/ОY^/, начала отсчета которых совпадают, а оси повернуты на некоторый угол φ_o (рис. 10).

 

 

рис. 10

 

Очевидно, что в обеих системах расстояния до начала отсчета одинаковы, а полярные углы связаны линейным соотношением

ρ^/ = ρ, φ^/ = φ − φ_o. (3)

 

Эти простые формулы и выражают преобразования координат при повороте осей. Получим также и формулы преобразования поворота для декартовых координат. Запишем выражения для декартовых координат в «штрихованной» системе отсчета

 

x^/ = ρ^/cosφ^/ = ρcos(φ − φ_o);

 

y^/ = ρ^/sinφ^/ = ρsin(φ − φ_o).

 

Используем известные тригонометрические формулы для синуса и косинуса разности углов:

 

x^/ = ρcos(φ − φ_o) = ρcosφcosφ_o + ρsinφsinφ_o;

 

y^/ = ρsin(φ − φ_o) = ρsinφcosφ_o − ρcosφsinφ_o.

Наконец, замечая, что

ρcosφ = x, а ρsinφ = y,

получим искомые выражения:

 

x^/ = xcosφ_o + ysinφ_o; y^/ = ycosφ_o − xsinφ_o. (4)

 

Заметьте, что формулы обратного преобразования получаются из системы (4) посредством очевидной замены φ_o на −φ_o, что также является следствием относительности координат. Эти преобразования, конечно, можно было получить и геометрическим способом с помощью приведенного рисунка.

Упражнения

1. Покажите, что формулы преобразования (4) не изменяют расстояния до начала координат.

2. Покажите, что расстояние между  двумя точками, полярные координаты которых (ρ₁, φ₁) и (ρ₂, φ₂), определяется по формуле

S = √{ρ₁² + ρ₂² − 2ρ₁ρ₂cos(φ₁ − φ₂)}.

Декарт Рене

Рене Декарт (фр. Ren? Descartes; лат. Renatus Cartesius − Картезий) − французский математик, философ, физик и физиолог, создатель аналитической геометрии и современной алгебраической символики, автор метода радикального сомнения в философии (рис. 14).

рис. 14

Декарт происходил из старинного, но обедневшего дворянского рода. Он родился 31 марта 1596 года в городе Лаэ во Франции. Его мать умерла, когда ему был один год. Воспитанием мальчика занималась бабушка по матери.

Начальное образование Декарт получил в иезуитском коллеже. Религиозное образование, как ни странно, только укрепило в молодом Декарте скептическое недоверие к тогдашним философским авторитетам. Позже он сформулировал свой метод познания − дедуктивные (математические) рассуждения над результатами воспроизводимых опытов.

В 1612 году Декарт закончил коллеж², некоторое время изучал право, затем уехал в Париж, где несколько лет чередовал рассеянную жизнь с математическими исследованиями. Затем в 1617 году он поступил на военную службу − сначала в революционную Голландию, затем в Германию, где участвовал в битве за Прагу во время тридцатилетней войны. Несколько лет Декарт провёл в Париже, предаваясь научной работе. Затем − ещё несколько лет участия в войне (осада Ларошели³). По возвращении во Францию оказалось, что свободомыслие Декарта стало известно иезуитам, и те обвинили его в ереси. Поэтому в 1628 году Декарт переехал в Голландию, где провёл 20 лет.

Он вёл обширную переписку с лучшими учёными Европы, изучал самые различные науки − от медицины до метеорологии. Наконец в 1634 году он закончил свою первую программную книгу под названием «Мир». Но момент для издания был неудачным − годом ранее инквизиция чуть не замучила Галилея. Теория Коперника, принятая и в книге Декарта, была официально запрещена. Поэтому Декарт решил при жизни не печатать этот труд.

Вскоре, однако, одна за другой появляются другие книги Декарта: «Рассуждение о методе...» (1637 г.); «Размышления о первой философии...» (1641 г.); «Начала философии» (1644 г.).

В «Началах философии» сформулированы главные идеи Декарта:

− бог сотворил мир и законы природы, а далее Вселенная действует как самостоятельный механизм;

− в мире нет ничего, кроме движущейся материи различных видов. Материя состоит из элементарных частиц, локальное взаимодействие которых и производит все природные явления;

− математика − мощный и универсальный метод познания природы, образец для других наук.

Кардинал Ришелье благожелательно отнёсся к трудам Декарта и разрешил их издание во Франции, а вот протестантские богословы Голландии наложили на них проклятие.

В 1649 году Декарт, измученный многолетней травлей за вольнодумство, поддался уговорам шведской королевы Кристины и переехал в Стокгольм. Почти сразу после переезда он серьёзно простудился и вскоре умер (11 февраля 1650 года). Предположительной причиной смерти явилась пневмония. Существует гипотеза об его отравлении, поскольку симптомы болезни очень сходны с симптомами при остром отравлении мышьяком.

К концу жизни Декарта отношение церкви к его учению стало резко враждебным. Вскоре после его смерти основные сочинения Декарта были внесены в «Индекс запрещенных книг», а Людовик XIV специальным указом запретил преподавание философии Декарта («картезианства») во всех учебных заведениях Франции.

Спустя 17 лет после смерти учёного его останки были перевезены в Париж (позже он был погребён в Пантеоне). В 1819 году многострадальный прах Декарта был вновь потревожен и ныне покоится в церкви
Сен-Жермен де Пре.

Научная деятельность Декарта очень разнообразна. В 1637 году вышел в свет главный математический труд Декарта − «Рассуждение о методе» (полное название − «Рассуждение о методе, позволяющем направлять свой разум и отыскивать истину в науках»). Символическую алгебру Декарт называл «Всеобщей математикой» и писал, что она должна объяснить «всё относящееся к порядку и мере».

Создание аналитической геометрии позволило перевести исследование геометрических свойств кривых и тел на алгебраический язык, то есть анализировать уравнение кривой в некоторой системе координат. Достоинства нового метода были исключительно велики, и Декарт продемонстрировал их в той же книге, открыв множество положений, неизвестных древним и современным ему математикам.

Вместе с конкретными научными открытиями было совершено ещё одно открытие. Обнаружилась необходимость и возможность постоянной работы над собственным умом, необходимость и возможность постоянного обращения мысли на мысль, постоянного развития самой способности мыслить, открывать, изобретать. Исходной точкой философских рассуждений Декарта является «сомнение во всем». Скептицизм был всегда выдающейся чертой французского ума, равно как и стремление к математической точности знаний.

Cogito, ergo sum (мыслю, следовательно существую) − есть первое и вернейшее из всех познаний, встречающееся каждому, кто философствует в порядке.

¹Для примера можно вспомнить знаменитый роман М. Булгакова «Мастер и Маргарита».

²А через год в России закончилась смута и на царский престол избран первый из Романовых − Михаил.

³Там он мог встречаться с «тремя мушкетерами» − Атосом, Портосом, Арамисом и Д'Артаньяном.

Материальная точка

Во многих кинематических задачах оказывается возможным пренебречь размерами самого тела. Еще раз рассмотрим автомобиль, движущийся из Минска в Брест. Расстояние между этими городами − порядка 350 километров, размеры автомобиля − несколько метров, поэтому в такой ситуации при описании положения автомобиля можно не учитывать его размеры (если капот автомобиля находится в Бресте у нужного подъезда нужного дома, то можно считать, что и его багажник находится приблизительно там же). Таким образом, в данной задаче можно мысленно заменить автомобиль его моделью − телом, размеры которого пренебрежимо малы. Такая модель тела очень часто используется в физике и называется материальной точкой.

Материальная точка − это идеальная модель тела, размерами которого в данных условиях можно пренебречь. Общим у геометрической и материальной точек является отсутствие собственных размеров. Материальную точку по мере необходимости можно «наделять» свойствами, которыми обладают реальные тела, например, массой, энергией, электрическим зарядом и так далее.

Одним из критериев применимости модели материальной точки является малость его размеров по сравнению с расстоянием, на которое перемещается тело. Однако это условие не является абсолютно однозначным. Так, описывая движение Земли вокруг Солнца при расчете ее положения на орбите, размерами Земли можно пренебречь, считая ее материальной точкой (рис. 15 − Николай Коперник и его гелиоцентрическая модель Солнечной системы.).

 

рис. 15

 

Однако если нам необходимо рассчитать времена  восхода и заката Солнца, модель материальной точки принципиально неприменима, так как это описание требует учета вращения Земли, ее размеров и формы (рис. 16. Восход Земли − вид с Луны).

 

 

рис. 16

 

Рассмотрим еще один пример. Спринтеры соревнуются на стометровой дистанции. Цель описания движения − выявить, кто из спортсменов пробегает дистанцию за меньшее время (то есть задача чисто кинематическая). Можно ли в данной задаче считать бегуна материальной точкой? Его размеры значительно меньше дистанции забега, но достаточно ли они малы, чтобы ими можно было пренебречь? Ответ на эти вопросы зависит от требуемой точности описания. Так, на серьезных соревнованиях время измеряется с точностью 0,01 секунды. За это время бегун смещается на расстояние порядка 10 сантиметров (простая оценка, полученная исходя из средней скорости спринтера 10 м/с). Следовательно, погрешность, с которой определяется положение бегуна (10 см), меньше, чем его поперечные размеры, поэтому модель материальной точки в данном случае неприменима. Не случайно мастера спринтерского бега на финише «бросают грудь вперед», выигрывая драгоценные сотые доли секунды (рис. 17. Есть мировой рекорд! У. Болд).

 

 

рис. 17

Упражнение.

Оцените, можно ли  использовать модель материальной точки, если время забега измеряется с точностью 0,1 с.

В некоторых ситуациях можно использовать модель материальной точки, даже если размеры тела сравнимы и больше расстояний, на которое смещается тело. Это допустимо тогда, когда положение одной точки тела однозначно определяет положение всего тела. Так, при скольжении бруска по наклонной плоскости можно найти положение всего тела, зная положение его центра (как, впрочем, и любой другой точки).

Если модель материальной точки оказывается неприменимой, то необходимо использовать другие, более сложные модели.

Абсолютно твердое тело

Многие реальные тела являются твердыми, то есть в течение длительного  времени сохраняют свои размеры и форму, точнее говоря, изменения размеров и формы настолько незначительны, что ими можно пренебречь. Моделью таких тел служит абсолютно твердое тело.

Абсолютно твердое тело − это идеальная модель тела, изменением размеров и формы которого в данных условиях можно пренебречь.

Из этого определения следует, что расстояние между двумя любыми точками абсолютно твердого тела остается неизменным. Абсолютно твердое тело можно также рассматривать как совокупность материальных точек, жестко связанных между собой. Так, положение океанского лайнера в открытом море можно описать, пользуясь моделью материальной точки, а его пространственную ориентацию (курс, наклон) − с помощью модели абсолютно твердого тела (рис. 18).

 

рис. 18

 

Применимость модели абсолютно твердого тела обусловлена только конкретной исследуемой проблемой − целью моделирования и требуемой точностью.

В заключение отметим, что рассмотренные нами модели не исчерпывают всех типов моделей тел, используемых в физике. Например, того же бегуна нельзя описать и в рамках модели абсолютно твердого тела, так как здесь важно взаимное расположение частей тела − туловища, рук, ног, головы и изменение этого положения. В таких ситуациях можно использовать модель, состоящую из нескольких движущихся друг относительно друга твердых тел и материальных точек (рис. 19).

 

 

рис. 19

Число степеней свободы тела

Теперь после того, как мы изучили несколько моделей тел, можно окончательно и корректно сформулировать ответ на вопрос о том, что значит задать, определить положение тела: указать численное значение координат некоторых точек тела так, чтобы положение всего тела (любой его части) было определено однозначно.

Число независимых координат, которые однозначно определяют положение тела или системы тел в пространстве, называется числом степеней свободы.

Число степеней свободы − очень важная характеристика описываемой системы хотя бы потому, что определяет число независимых уравнений, описывающих движение системы.

Подсчитаем число степеней свободы некоторых простых систем.

Материальная точка, по определению, не имеет размеров, поэтому ее положение в пространстве определяется однозначно тремя координатами. Следовательно, число степеней свободы свободно материальной точки равно трем.

Если на движение материальной точки накладываются дополнительные условия, то число ее степеней свободы может уменьшиться. Так, если точка движется по заданной поверхности, то ее положение определяется двумя независимыми координатами. Следовательно, число степеней свободы равно двум; при движении по заданной линии число степеней свободы уменьшается до одной. Подчеркнем, это не значит, что при движении по заданной линии может изменяться только одна − и могут изменяться все три, но положение точки на заданной линии определяется одной координатой, и если она известна, то могут быть определены и две другие. Тем не менее описание положения точки на заданной линии с помощью одной координаты оказывается не всегда удобным. Ценность рассмотренных нами декартовых координат в том, что они позволяют установить физические законы, описывающие движение вдоль всех прямых (все прямые одинаковы!). В то же время для описания изменения координат на произвольной линии пришлось бы записывать свои законы для каждой линии − окружности, параболы, синусоиды и т. д. Поэтому часто одномерное движение вдоль известной линии описывают с помощью двух или трех координат. Однако и в этом случае число степеней свободы остается равным единице.

Если механическая система может быть промоделирована как совокупность материальных точек, движущихся в пространстве, то очевидно, что полное число ее степеней свободы равняется – 3N. Но если на движение этих материальных точек накладываются дополнительные ограничения, то число степеней свободы уменьшается.

Рассмотрим, как можно описать положение в пространстве двух материальных точек, жестко связанных между собой (что-то похожее на гантели) (рис. 20).

 

рис. 20

Две точки имеют шесть степеней свободы, которые могут быть описаны шестью координатами − х₁, у₁, z₁, х₂, y₂, z₂, но так как расстояние между точками неизменно, то на эти координаты накладывается условие:

 

(x₁ − x₂)² + (y₁ − y₂)² + (z₁ − z₂)² = l²,