
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моделирование многомерных случайных данных
Если y – случайная величина с математическим ожиданием m и дисперсией σ2, то x = (y – m)/σ - случайная величина с математическим ожиданием 0 и дисперсией 1, y = m +σ x. Если Y – r -мерный случайный вектор со средним m и ковариационной матрицей Σ, то X = Σ-1/2(Y - m) - r -мерный случайный вектор со средним 0 и ковариационной матрицей E (операция «отбеливания» вектора Y), Y = m + Σ1/2 X. Если функция «квадратный корень из матрицы» недоступна, поступаем следующим образом. Пусть Q -диагональная матрица, на диагонали которой стоят собственные числа Σ,
P – матрица, столбцами которой являются нормированные собственные векторы S. Построим матрицу
Тогда S 1/2=
Замечание. Имеется следующий распространенный источник ошибок при моделировании векторных выборок. Если имеются случайные величины x, y со средним 0, СКО σ x, σ y и число
всегда является ковариационной матрицей случайного вектора
можно прийти к противоречию. Критерий корректности задания Пример 3.3. Организовать процедуру эмуляции серии значений вектора X из задачи 3.2 и вычислить по методу Монте-Карло вероятность попадания этого вектора в треугольник с вершинами (0,0), (2,1), (1,3).
Задания на лабораторную работу 1. Решить приведенные ниже задачи. Привести вычисления и иллюстрации в ИМС MatLab. 2. Задать 2 набора значений СКО и коэффициентов корреляции. Сформировать 2 3-мерные ковариационные матрицы. Проверить непротиворечивость. 3. Сформировать 2 3-мерных облака точек как выборки объемом 1000 из заданных таким образом нормальных законов. 4. Получить выборочные оценки параметров. Дать графические иллюстрации. Контрольные вопросы 3.1. Построить для вектора X из задачи 2 доверительный эллипс с уровнем значимости 0.9. 3.2. D ={(x,y): -1< x <2, 0< y <2.5}. 3.3.
|
|||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 217; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.102.112 (0.004 с.) |
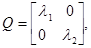
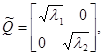
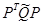 . Это позволяет, в частности, моделировать выборки из r -мерного нормального закона Nr (m,Σ), используя стандартный датчик нормально распределенных случайных чисел X = randn(r, n).
. Это позволяет, в частности, моделировать выборки из r -мерного нормального закона Nr (m,Σ), используя стандартный датчик нормально распределенных случайных чисел X = randn(r, n). 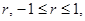 то матрица
то матрица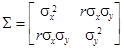
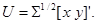 Если же величин три или больше, то коэффициенты корреляции между ними нельзя задавать произвольно. Например, если пары величин (x, y) и (y, z) связаны сильной положительной связью, то связь в паре (x, z) не может оказаться отрицательной. Это значит, что, задавая ковариационную матрицу трехмерного случайного вектора в виде
Если же величин три или больше, то коэффициенты корреляции между ними нельзя задавать произвольно. Например, если пары величин (x, y) и (y, z) связаны сильной положительной связью, то связь в паре (x, z) не может оказаться отрицательной. Это значит, что, задавая ковариационную матрицу трехмерного случайного вектора в виде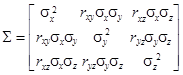 ,
,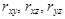 состоит в том, что все собственные числа матрицы Σ должны быть больше или равны 0.
состоит в том, что все собственные числа матрицы Σ должны быть больше или равны 0.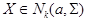 , k = 2, a = [1 2] T, σ12 = 1, σ22 = 2, ρ = 0. Найти вероятность попадания этого вектора в прямоугольник
, k = 2, a = [1 2] T, σ12 = 1, σ22 = 2, ρ = 0. Найти вероятность попадания этого вектора в прямоугольник


