
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Равномерная непрерывность функции на множестве. Теорема кантора о равномерной непрерывности функции.
⊐ ф.f опр на Х⊂R f непр на Х⇔"хϵХ "e>0 $d>0 "yϵX, |x-y|<d ↝|f(x)-f(y)|<0 Здесь d>0 зависит от e и от х, т.е. d=d(х,e) Если f(x)= Определение: если в определении непрерывности f на х удлиняется по заданному e>0 найти d>0 общее для "х, то f-равномерно непрерывна на х. f равномерная непрерывность на Х: "e>0 $d>0: "x yϵX, |x-y|<d®|f(x)-f(y)|<e "x $d $d "x f не равномерно непрерывна на Х⇔$e>0 "d>0, $x,y т.ч. |x-y|<d, но |f(x)-f(y)|≥e
Теорема Кантора: если f непрерывна на отрезке [a,b],то f равномерно непр на [a,b] Док-во: (от противного): допустим, что f неравномерно непр на [a,b] ↝$ {
Рассмотрим п\посл По непрерывности f в точке с 26. Определение f'( Опр: 1) ⊐ f опр на Е⊂R, Если $ кон.предел
2) Если этот lim $ для " x- Правила дифференцирования: 1) 2) h=f+g→h’( 3) h=f*g→h’( 4) h= 5) f(x)-f(
Дифференцируемые функции. Уравнение касательной прямой к графику функции. Определение: f При этом (будет доказано) если $ число А:
(df( Теорема: f дифференциал в точке равно A=
⇒ f дифференциал в точке Пусть f определена на Е⊂R, Касательная прямая к графику функции через точку ( y- Определение: y= т.е. f(x)-f( т.е. f дифференциал в точке Т.о. у графика f в точке
Производная суперпозиции функций. 1) ⊐ Теорема: если $ f'( Док-во:
g(
= ∆x→0 (∆x→0↝∆y=f( $ 1) h(x)=sin( h’(x)=cos( 2) h(x)= h’(x)=2sinx*cosx=sin2x 2) производная показ. функция f(x)=U
( f(x)= f(x)= f’(x)= Теорема Ферма, Ролля, Лагранжа и Коши. Теорема Ферма: ⊐ f определена на <a,b>; cϵ(a,b) и выполняется: 1) f дифференциал в точке с 2) Тогда
Замечание: если в условии теоремы выполнено только 2), то либо
Теорема Ролля: ⊐ f непрерывна [a,b] дифференциал в (a,b), причем f(a)=f(b) (на концах принимают одиночные значения) Тогда $ сϵ(a,b), такое что По т.В-са для f $ наибольший (М) и наименьший (m) значения на [a,b] 1) если m=M ↝ f(x)=m(const) ↝ 2) ⊐ m<M, тогда хотя бы 1 значение принимает внутри М=f(c) где сϵ(a,b)↝c-т.max Теорема Лагранжа: ⊐ f непрерывна на [a,b], дифференциал в (a,b)⇒$cϵ(a,b) Формула Лагранжа f(b)-f(a)=
Рассмотрим функцию j(a)=j(b)↭f(a)-lb↝= По т.Ролля с этим числом $ сϵ(a,b) т.ч.
a<c<b ⊐ b<c<a c=a+θ(b-a) – x++∆x (∆x≥0) f(x+∆x)-f(x)= Правила Лопиталя. Теорема 1: ⊐ функции f,g определены на (a,b>
3) 4) 5) $ Тогда $
Тогда f,g непрерывны на [a,b> и дифференциалы в (a,b) Рассмотрим a<x<b на [a,b] можем применить теорему Коши
Теорема 2: ⊐ f,g определены на <c,∞)
3) 4) 5) $ Тогда ⊐ ⊐ t= 1) 2)
3) 4) 5) Теорема 3: ⊐ f,g определена на (a,b> (-∞≤a)
3) 4) 5) $ Скорость стремления
2)
|
||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 87; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.184.0 (0.027 с.) |
 , x=(0;∞), то d<x рисунок
, x=(0;∞), то d<x рисунок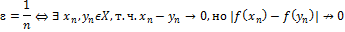
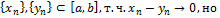 |
| 
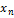 }⊂[a,b]↝ {
}⊂[a,b]↝ { 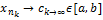
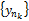 с теми же наименованиями ↝
с теми же наименованиями ↝ 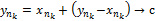
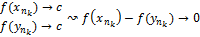
 , правила дифференцирования.
, правила дифференцирования.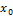 ϵE-предельная точка Е
ϵE-предельная точка Е -производное число f в точке
-производное число f в точке 
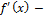 произ.ф-я f (на Е)
произ.ф-я f (на Е)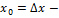 приращение аргумента ↝ х=
приращение аргумента ↝ х= 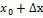
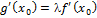

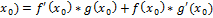
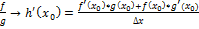
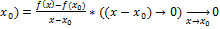
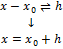
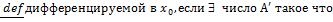
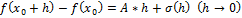
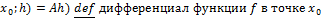
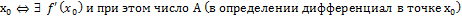

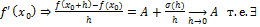
 a(h)=
a(h)= 
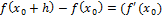 →A)*h+((a(h)*h)=σ(h)(h→)) (верно h=0, т.е. fдифференциал в
→A)*h+((a(h)*h)=σ(h)(h→)) (верно h=0, т.е. fдифференциал в 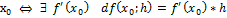
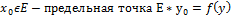

 рисунок
рисунок
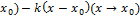

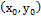 $ прямая ⇔ f дифференциал в
$ прямая ⇔ f дифференциал в  )
)

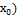 и $ g’(
и $ g’( , то $ h'(
, то $ h'(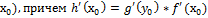
 -f(
-f(
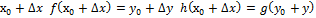 т.к. дифф. в
т.к. дифф. в 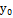 то
то 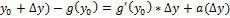 *(∆y) (a(∆y)
*(∆y) (a(∆y)  0)
0)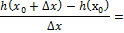

 в силу непрерыв f в
в силу непрерыв f в 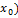
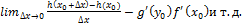

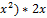
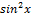
 (U(x)>0)
(U(x)>0)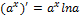
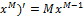
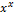 ↝
↝ 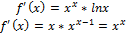


 окрестность U=U(c) т.е. f(c)≥f(x) "xϵU
окрестность U=U(c) т.е. f(c)≥f(x) "xϵU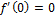
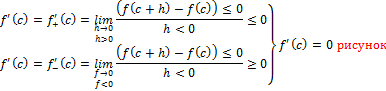
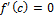 , либо
, либо 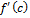 не $ (критическая точка)
не $ (критическая точка)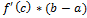
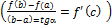 рисунок
рисунок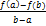

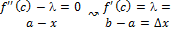 =
= 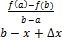 рисунок
рисунок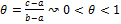
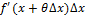

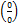 ®расрытие неопределенностей x®
®расрытие неопределенностей x® 
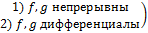 на (a,b>
на (a,b>

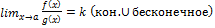

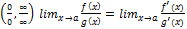 если правда lim $, то определим f,g в т. а положив f(a)=g(a)=0
если правда lim $, то определим f,g в т. а положив f(a)=g(a)=0 a<x<b®
a<x<b® 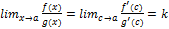

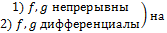 <c,∞)
<c,∞)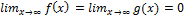

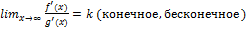
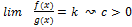

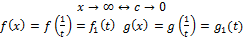
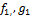 непрерывны на
непрерывны на 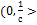 как суперпозиция непрерывных функций
как суперпозиция непрерывных функций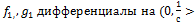
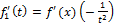
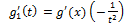

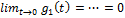

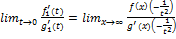 =k по т.1 ⊐
=k по т.1 ⊐ 
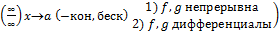 на (a,b>
на (a,b>
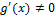

 рисунок
рисунок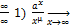 + ∞
+ ∞ 
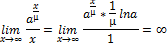

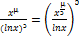
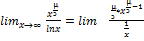 =
= 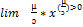 = + ∞
= + ∞


