Величина — понятие аксиоматическое

Учителя подводят учеников к решению задачи на основе сравнения массы перевозимых грузов, затем — скорости, и решение принимает вид:

Однако смысл последнего выполняемого действия в решении задачи трудно доходит до сознания учащихся. Для осознанного решения учащиеся должны усвоить основные понятия, связанные с той или иной ситуацией, и установить взаимосвязь между величинами, входящими в задачу. На данном этапе обучения это сделать слишком трудно, а может быть, и невозможно. Задача приведена в качестве примера, позволяющего осознать, что вопрос: «О каких величинах идет речь в задаче?» нужно использовать крайне осторожно.

В последнее время в некоторых альтернативных программах используется термин решение задач на процессы (вместо — задачи на работу, на движение и т.п.). Поэтому при решении задач иногда можно услышать и такие вопросы: «Что можно узнать, если известны скорость процесса и его результат?», «Как найти результат процесса, если известны скорость и время процесса?»

Действительно, в некоторых задачах на движение, на покупку и т.п. описываются процессы, которые характеризуются системой из трех величин, связь между которыми осуществляется с помощью одного и того же равенства вида: а = b с, (b = а: с, с = а: b). Приведем в качестве примера следующие задачи

 

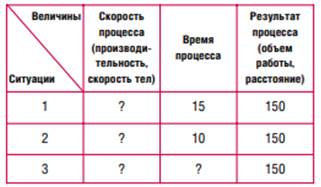
Как видим, первая задача относится к задачам на работу, вторая — на движение, а третью можно отнести как к первому, так и ко второму виду, поскольку рабочие при выполнении работы могут двигаться навстречу друг к другу.

Эти задачи отличаются по сюжету (в них включены различные величины), но они имеют одинаковые модели и структуры. Для ответа на вопросы этих задач необходимо установить связи и отношения между величинами, характеризующие процесс, о котором идет речь в каждой из задач. Анализ задач целесообразно начинать с выделения величин в предложенных ситуациях и установления связей и отношений между величинами, входящими в задачи. Построим обобщенную модель задач: запишем кратко условие задачи в виде таблицы.

 

Построенная таблица (модель задач) помогает устанавливать связи и отношения между величинами, входящими в задачу, сравнивать задачи с точки зрения метода решения, а также взаимно-однозначного соответствия между различными системами величин.

Опора на формулы помогает учащимся находить ответ задачи и подготавливает их к решению задач с помощью уравнений в старших классах. Но излишнее увлечение формулами в младших классах приводит к формальному пониманию хода решения. Поэтому во многих методических пособиях рекомендуется использовать формулы в качестве вывода, но не основы решения задач, так как решение по готовым формулам оказывает негативное влияние на развитие словесно-логического мышления, на формирование общего умения решать задачи у младших школьников.

Оценка площади

Автор: Т.В Зайцева

Журнал: Начальная школа №12 2012 год

Ссылка: https://n-shkola.ru/archive/viewarticle/481

 

 

Муравьи.

Автор: Л.В. Рулевская

Выходные данные: журнал начальная школа. 2000 год, 5 выпуск

Ссылка: https://n-shkola.ru/storage/archive/1407917517-2144470516.pdf

 

Величина — понятие аксиоматическое

Автор: В.С. Самойлов

Журнал: Начальная школа. 2005. № 7

Ссылка: https://n-shkola.ru/archive/view/149

Понятие величина всегда в той или иной степени рассматривалось в курсе арифметики, начиная с момента появления соответствующих учебников (в России таковые появились в начале XVIII в.), а затем с 70х годов прошлого столетия и в курсе математики начальных классов. Термин величина стал широко использоваться в курсе математики в начальной школе в связи с необходимостью общей трактовки этого понятия в различных дисциплинах. В курсе арифметики использовался другой тер мин — именованное число, который и сей час можно встретить в обучении математике в начальных классах. В большинстве учебников математики (например, учебники авторского коллектива под руководством М.И. Моро), по кото рым обучение начинается с изучения нумерации натуральных чисел первого десятка, сравнение величин и действий с величина ми, как правило, сводятся к соответствующим операциям над числовыми значения ми, т.е. проводятся опосредованно. И лишь в некоторых случаях сравнение производится непосредственно, например, с помощью наложения. Несмотря на то что вели чины в указанных учебниках в основном отождествляются с числовыми значениями величин, постепенно у учащихся формируется представление о самих величинах: длине, площади, массе и т.д. При этом четкого обоснования связи величин и чисел (всякую величину a при выбранной единице измерения е можно представить в виде a = kе), непосредственного и опосредованного способов сравнения величин (если две величины находятся в отношении «больше», то и соответствующие числовые значения находятся в таком же от ношении) не приводится. Указанные связи постепенно раскрываются в практических действиях над величинами. Совершенно другой подход наблюдает ся в учебниках математики для начальных классов, написанных в соответствии с системой Д.Б. Эльконина — В.В. Давыдова (авторы В.В. Давыдов, О.В. Савельева, Г.Г. Микулина, С.Ф. Горбов). По этим учебникам курс математики начинают изучать с величин и их основных свойств. Сложение, вычитание, сравнение геометрических (длина, площадь) и физических величин (масса, время, емкость) проводятся с помощью практических действий: откладывания суммы отрезков, наложения отрезков, сравнения масс с помощью весов, уравнивания масс на весах и др., — в ходе которых выявляются и обобщаются основные свойства величин (сравнимость, возможность складывать, переместительное и сочетательное свойства сложения, возможность вычитать из большей величины меньшую, неизменяемость суммы при за мене равных величин на равные, монотонность сложения), которые затем используются в качестве средства для изучения чисел, действий над ними и законов этих действий. Трудность, а во многих случаях невозможность непосредственного сравнения величин позволяет мотивировать введение понятия числа, после чего действия над величинами более обоснованно сводятся к действиям над числовыми значениями величин при выбранной единице измерения. Таким образом, понятие величины как одно из важнейших математических понятий может служить теоретической основой для введения понятия числа и изучения действий с числами. При сравнении методик формирования понятия числа в различных учебниках математики для начальных классов невольно возникает вопрос: что в своей практической деятельности человек начал использовать раньше — числа или величины? Ответ на этот вопрос склоняется в пользу величин, так как первоначально человек встретился с необходимостью сравнивать расстояния, длины предметов, например, при изготовлении стрел одинаковой длины. Позднее люди научились считать предметы, а вместе с ними и именованные числа. Наименование здесь выступало в роли единицы счета, или, как мы теперь говорим, единицы измерения величины. Другими словами, именованные числа — это форма представления величин. Числа как таковые еще не выделялись, они использовались только вместе с наименованиями. Чтобы получить числа в «чистом виде», необходимо было «оторвать» их от наименований, рассмотреть операции над ними и их свойства. Эта работа была проделана успешно в период образования научных школ в Древней Греции и в странах Дальнего Востока. Обобщению творчества математиков школ Древней Греции посвящен знаменитый труд Евклида «Начала». Здесь приводится и первое аксиоматическое определение величины. Перечислим аксиомы Евклида, описывающие общие свойства положительных скалярных величин: — равные одному и тому же равны между собой; — если к равным прибавить равные, то и целые будут равны; — если от равных отнимаются равные, то и остатки будут равны; — если к неравным прибавляются равные, то и целые будут не равны; — удвоенные одного и того же равны между собой; — половины одного и того же равны между собой; — совмещающиеся друг с другом равны между собой; — целое больше части. Представленная система аксиом в целом не удовлетворяет современным требованиям к подобного рода системам, так как она является зависимой и не является полной (например, четвертая аксиома является следствием второй). Однако математическая теория Евклида до сих пор привлекает внимание историков, методистов, а также самих математиков, так как обладает значительными дидактическими достоинствами: геометрический язык позволяет в тесной связи рассматривать арифметические, геометрические и алгебраические факты; достаточно простой язык позволяет использовать его в школьных курсах математики. Видимо, поэтому геометрический язык все больше места занимает в школьных учебниках математики начальных классов, все чаще можно услышать рассуждение учащихся с логическим клише: «если к равным прибавить равные, то и получатся равные». После Евклида многие известные математики (Архимед, Герон, Л. Эйлер и др.) пытались определить понятие величины, выделяя те или иные видовые отличия величины. Например, Герон Александрийский (I в.) утверждал, что величина есть все, что может быть увеличено или разделено безгранично, Л. Эйлер (XVIII в.) называл величиной все, что может увеличиваться или уменьшаться. До сих пор существуют попытки определить понятие величины, положив в основу только одно свойство, например, свойство сравнимости. В частности, в свое время о таких величинах писал академик А.Н. Крылов, соотнося их с такими свойствами, как красота, безобразие, храбрость, трусость и т.д. Не вольно вспоминается А.С. Пушкин: «Кто на свете всех милее, всех румяней и белее?» Обобщением различных попыток определить понятие величины является система аксиом замечательного российского ученого, академика А.Н. Колмогорова (1903–1987), которую он опубликовал в Большой советской энциклопедии в 1951 г. В этой аксиоматике первоначальное понятие «величина» является обобщением понятий длины, площади, массы и т.п. Каждый род величины связан с определенным способом срав нения физических тел и других объектов. В пределах каждой из рассматриваемых систем однородных величин отношение a < b и операция a + b = c обладают следующими свойствами. 1) Каковы бы ни были a и b, имеет место одно и только одно из трех соотношений: a = b, или a < b, или b < a. 2) Если a < b и b < c, то a < c (транзитивность отношения меньше). 3) Для любых величин a и b существует однозначно определенная величина c = a + b. 4) a + b = b + a (коммуникативность сложения). 5) (a + b) + c = a + (b + c) (ассоциативность сложения). 6) a + b > a (монотонность сложения). 7) Если a > b, то существует одна и толь ко одна величина c, для которой b + c = a. 8) Каковы бы ни были величина a и натуральное число n, существует величина b, что nb = a (возможность деления). 9) Каковы бы ни были величины a и b, существует натуральное число n, такое, что a < nb. Это свойство называют аксиомой Евдокса, или аксиомой Архимеда. 10) Если последовательность величин a1 < a2 <... < b2 < b1 обладает тем свойством, что bn – an < c для любой величины c при достаточно большом номере n, то существует единственная величина x, которая больше всех ai и меньше всех bi. Это свойство называют аксиомой Г. Кантора. В энциклопедии не приведено анализа этой системы аксиом с точки зрения их независимости, непротиворечивости и полно ты. В математической литературе есть лишь доказательство независимости аксиомы Архимеда от других аксиом. Например, в энциклопедии указано, что значение аксиомы Архимеда выяснилось с полной отчетливостью после того, как в XIX в. математики Веронезе, ЛевиЧивита и Гильберт обнаружили существование неархимедовых величин, т.е. таких, у которых все аксиомы Архимеда выполняются1. В исследовании Д. Гильберта «Основания геометрии» речь идет о независимости аксиомы Архимеда от геометрических аксиом. Построенная модель неархимедовой геометрии показывает существование неархимедовых величин. Специальные исследования о независимости системы аксиом величин нам неизвестны. Высокий уровень абстракции приведенных выше аксиом, использование сов ременного математического языка, значительное число аксиом в колмогоровской системе привели к потере дидактических достоинств изложения учения о величинах, которые были у Евклида, и сделали подход, в котором величины являются ос новой арифметики, неприемлемым не только для школьного преподавания, но и для студентов нематематических специальностей. Учитывая сказанное, мы попытались провести анализ системы аксиом и сделали вывод, что рассматриваемая аксиоматика не удовлетворяет современным требованиям, предъявляемым к подобного рода системам, так как является зависимой. Например, единственность разности (аксиома 7), единственность существующего отношения (аксиома 1) могут быть доказаны с помощью других аксиом. Рамки журнальной статьи не позволяют нам подробно изложить указанный анализ, поэтому далее мы приводим его результат — аксиоматическое определение величины. Множество V, рассматриваемое вместе с определенными на нем отношениями «< b, a = b, b < a. 2. Если к равным величинам прибавить равные, то получатся равные величины: a = a, b = b ⇒ a + b = a+ b 3. Сумма трех величин не зависит от по рядка их сложения (аксиома ассоциативности). a + b + c = s ⇒ a + (b + c) = s 4. Если b < a, то существует величина c, которая в сумме с b дает величину a (аксиома существования разности). (∀a, b ∈ V) (b < a) ⇒ (∃c ∈ V) (a = b + c) 5. Если прибавить, то получится больше, чем было (аксиома монотонности). (∀a, b ∈ V) (a + b > a) 6. От перемены мест слагаемых сумма не меняется. a + b = s ⇒ b + a = s 7. Для любых величин a и b существует конечная сумма c = a + a +... + a, такая, что c > b. (∀a, b ∈ V) (∃c = a + a +... + a) (c > b) Перечисленные 7 аксиом полностью определяют понятие аддитивной положительной скалярной величины. С их помощью могут быть докaзаны все остальные свойства. В частности, можно доказать, что «равно» является отношением эквивалентности, а «меньше» — отношением порядка. Рассматриваемая система аксиом может быть представлена еще более компактно. Например, учитывая то, что предложения 4 и 5 взаимно обратны, их можно объединить с помощью связки «тогда и только тогда». Эти аксиомы могут быть положены в основу построения натуральных и рациональных чисел. Для построения множества действительных чисел необходима еще одна аксиома — аксиома непрерывности, которую мы формулируем для отрезков следующим образом. 8. Какова бы ни была бесконечная последовательность вложенных друг в друга отрезков, существует хотя бы одна точка, которая является внутренней точкой всех этих отрезков. Есть и другие подходы к определению понятия аддитивной скалярной величины. Они, как правило, связаны с рассмотрением множества объектов с заданными на нем какимилибо отношениями: эквивалентности, порядка, тернарного отношения a = b + c. К таковым относится и определение Н.Я. Виленкина, опирающееся на понятие области определения величины Ω (предполагается, что на указанной области определено отношение эквивалентности «равновеликость» и тернарное отношение «+»). Приведем это определение: «Величиной, заданной отношениями a b и a = b + c в множестве Ω, называется разбиение этого множества на классы эквивалентности по отношению «a равновелико b»1. Отметим, что этот и другие аналогичные подходы также являются аксиоматически ми, так как предполагают выполнимость рефлексивности, симметричности, транзитивности и других свойств заданных отношений, поэтому при детальном изложении требуют рассмотрения примерно такого же количества аксиом, что и в приведенной выше аксиоматике. Кроме того, необходимо констатировать, что определение Н.Я. Виленкина не может служить теоретической основой для построения курса математики по системе В.В. Давыдова, так как предполагает построенной систему действительных чисел. Таким образом, существующие подходы к определению понятия величины — аксиоматические. Это означает, что не существует какого-либо свойства, которое могло бы служить единственным видовым отличием для величины. Одной из причин этого явления следует считать приложимость понятия величины к слишком широкому кругу свойств. Можно доказать эквивалентность указанных подходов к определению понятия величины. Все сказанное говорит об имеющихся возможностях построения достаточно интересной теории скалярной величины для студентов — будущих учителей начальных классов. Таким образом, понятие скалярной аддитивной величины — это неопределяемое понятие, которое находит свое наиболее полное описание с помощью одной из систем аксиом. Мы полагаем, что будущих учителей начальных классов необходимо знакомить с различными подходами к определению понятия величины и следует показать эквивалентность этих подходов. В частности, на занятиях необходимо подчеркнуть, что изучаемые в школе величины выступают как свойства объектов и при выполнении определенных аксиом они становятся аддитивными скалярными величинами.