
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Колебания систем с двумя степенями свободы
Уравнения перемещений масс имеют вид:
Здесь δ - единичные перемещения, а Р – силы инерции масс в случае собственных колебаний: Так как при собственных колебаниях уравнения перемещений аналогично (15.6) имеют вид
Приравнивая определитель этой системы нулю, получим биквадратное частотное уравнение
Корни этого уравнения определяют две частоты собственных колебаний – меньшую ω1 и большую ω2. Из системы уравнений (15.4) следует, что между амплитудами колебаний существует определенная зависимость
Частоте ω1 соответствует коэффициент
В этой системе четыре неизвестных – две амплитуды и две начальные фазы. Умножая первое и второе уравнения системы (15.43) на k 2 и вычитая из них третье и четвертое уравнения при условии
По амплитудам и частотам колебаний можно вычислить силы инерции и выполнить динамический расчет прочности балки. В частном случае симметричной системы, когда
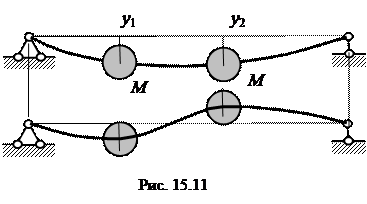
Этим частотам соответствуют коэффициенты k 1 =1 и k 2 =-1, определяющие две формы колебаний – симметричную с низшей частотой колебаний ω1 и кососимметричную с частотой ω2, рис. 15.11:
 . (15.45) . (15.45)
Дважды дифференцируя уравнения движения (15.45), можно найти ускорения, а затем и силы инерции колеблющихся масс:
В случае вынужденных колебаний (без учета сопротивления движению) от заданной гармонической нагрузки система амплитудных уравнений (15.40) будет неоднородной:
Отсюда находим амплитуды вынужденных колебаний:
Здесь главный определитель системы
Поперечные колебания систем с распределенными параметрами
Используем приближенное дифференциальное уравнение изогнутой оси балки, рис. 15.12.
и дважды его дифференцируем
Здесь Если возмущающей нагрузки нет, когда
|
||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 68; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.113.197 (0.01 с.) |
 Примером такой системы может быть невесомая балка с двумя сосредоточенными массами М 1 и М 2, рис. 15.10.
Примером такой системы может быть невесомая балка с двумя сосредоточенными массами М 1 и М 2, рис. 15.10. ,
, .
. и
и  .
.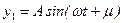 и
и  , то, подставляя силы инерции
, то, подставляя силы инерции 
 и
и  в уравнения перемещений, получим систему амплитудных перемещений:
в уравнения перемещений, получим систему амплитудных перемещений: , (15.40)
, (15.40) .
.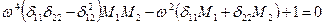 .
. (15.41)
(15.41) . (15.42)
. (15.42) , а частоте ω2 – k 2 = B 2 / A 2. Так можно найти уравнения движения масс и скоростей движения:
, а частоте ω2 – k 2 = B 2 / A 2. Так можно найти уравнения движения масс и скоростей движения: ,
, ,
, ,
, . (15.43)
. (15.43) ,
, 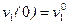 ,
,  ,
, 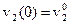 находим амплитуды колебаний и начальные фазы:
находим амплитуды колебаний и начальные фазы: ,
, ,
, , (15.44)
, (15.44) .
. , из (2.3) найдем:
, из (2.3) найдем: ,
,  .
.
 ,
, .
. С учетом перемещений (15.45) получаем:
С учетом перемещений (15.45) получаем: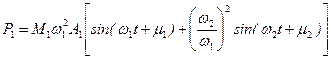 ,
,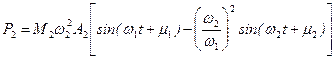 .
.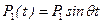 и
и 
 ,
, .
. ,
,
 .
. Системами с распределенными параметраминазываются системы с бесконечным количеством сосредоточенных масс или системы с массой распределенной по известному закону. Ограничимся рассмотрением систем с равномерно распределенной массой интенсивностью m.
Системами с распределенными параметраминазываются системы с бесконечным количеством сосредоточенных масс или системы с массой распределенной по известному закону. Ограничимся рассмотрением систем с равномерно распределенной массой интенсивностью m.
 . (15.46)
. (15.46)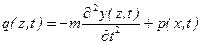 - интенсивность сил инерции от распределенной массы и возмущающей нагрузки.
- интенсивность сил инерции от распределенной массы и возмущающей нагрузки. , то получим дифференциальное уравнение движения сечений балки при собственных колебаниях.
, то получим дифференциальное уравнение движения сечений балки при собственных колебаниях.


