
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет тонкостенных оболочек по безмоментной теории
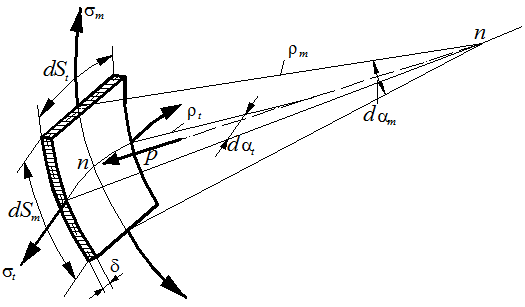
Рассмотрим тонкостенную осесимметричную оболочку, испытывающую действие внутреннего давления жидкости или газа (рис. 13.1) Выделим из этой оболочки двумя кольцевыми и двумя меридиональными сечениями бесконечно малый элемент, и рассмотрим его в равновесии (рис.13.3).
Рис. 13.3
Принимая во внимание осевую симметрию оболочки и полярно симметричную нагрузку в меридиональном и кольцевом направлении, можно полагать, что по сечениям отсутствуют деформации сдвига. Следовательно, касательные напряжения по таким сечениям будут равны нулю. По граням рассматриваемого элемента действуют только нормальные напряжения, вызванные двумя растягивающими продольными усилиями в двух взаимно перпендикулярных плоскостях. На площадках окружных сечений действуют меридиональные напряжения σ m, а на меридиональных площадках - окружные напряжения σ t. Меридиональным σ m называется такое нормальное напряжение, которое действует в оболочке в меридиональном направлении. Кольцевым σ t называется такое нормальное напряжение, которое действует в оболочке в кольцевом направлении. Напряжения σ m и σ t, как сказано выше, распределены по площади сечений равномерно. Срединная поверхность оболочки является поверхностью двоякой кривизны. Радиус кривизны в меридиональном направлении обозначим через ρm ,, а в окружном – ρt . (рис. 13.3). На внутреннюю поверхность оболочки действует распределенная нагрузка, равнодействующая которой равна dP = p dSm dSt Равнодействующая нормальных напряжений по меридиональным сечениям dNt = σ m dFt = σ m d St δ Аналогично по кольцевым сечениям dNm = σ t dFm = σ t dSm δ
Запишем условие равновесия элемента, спроектировав все силы на ось nn. S Fnn =2 Nt sin d α m /2+ 2 Nm sin d αt/2 – dP = 0 2σ m d St δ sin d α m /2 + 2 σ t dSm δ sin d α t /2 – p dSm dSt = 0 13.1 Ввиду малости углов и можно записать sin d αt/2= d αt/2, sin d α m /2 = d α m /2
После преобразований получим
Это уравнение получено французским астроном и физиком Лапласом в начале XIX века, который решал задачу, связанную с поверхностным натяжением в жидкостях. Аналогичность этих явлений состоит в том, что пленка в капле жидкости, как и стенке оболочки, испытывают растяжение, удерживая в равновесии некоторый объем жидкости. Этим можно объяснить применение в практике строительства каплевидных резервуаров, обладающих рядом преимуществ по сравнению с другими формами оболочек. Однако изготовление каплевидных резервуаров представляет определенные трудности. Формула (13.2) содержит два неизвестных σ m и σ t. Для определения меридионального напряжения σ m рассмотрим (рис. 13.1 б). Нижняя часть отсеченной оболочки находится в равновесии. Следовательно,
S F оо = σ m 2π R δ cos α – p π R 2 – – Q = 0 13.3
отсюда Здесь: Q – вес части сосуда и жидкости, расположенных ниже рассматриваемого сечения, P - давление в жидкости, определяемое по закону Паскаля с учетом избыточного давления по сравнению с атмосферным – q, γ – плотность жидкости. p = γ h + q
Используя формулы (13.2) и (13.4) можно найти меридиональные и окружные напряжения в оболочке. Нормальные напряжения σ m и σ t, действующие по площадкам, на которых отсутствуют касательные напряжения, являются главными. Третье главное напряжения изменяется в пределах: ноль на наружной поверхности оболочки до значения р на внутренней поверхности. В тонкостенных оболочках σ m и σ t значительно больше р, поэтому значением главного напряжения σ3 пренебрегаем. Следовательно, материал тонкостенной оболочки находится в плоском напряженном состоянии. Давая оценку прочности оболочки, будем пользоваться четвертой теорией прочности
|
||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 118; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.204.208 (0.005 с.) |
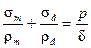 13.2
13.2 13.4
13.4 13.5
13.5


