
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод непосредственного интегрирования при определении перемещений в балках. Граничные условия
Остановимся на применении уравнения (9.4) при определении прогибов и углов поворота сечений балки методом непосредственного интегрирования. Это уравнение есть дифференциальное уравнение второго порядка с разделенными переменными. Поэтому его интегрирование выполняется по довольно простой схеме. Первый интеграл позволяет найти углы поворота φ(z), т.е.:
Вторичное интегрирование дает возможность найти функцию прогиба v (z):
Формулы (а) и (б) содержат две произвольные постоянные интегрирования С 1 и С 2., которые можно найти из граничных условий для функций прогиба и угла поворота в балке, вытекающих из условия закрепления балки идеальными связями.
Для балки на рис. (9.4, а) имеем: при z=a, прогиб v= 0; при z=l+a, прогиб v= 0. Для балки на рис. (9.4, б) при z=l, прогиб v= 0; угол поворота φ = 0 Для балки на рис. (9.4, в) при z = a, прогиб v=0; при z =l, угол поворота φ=0 Таким образом, для каждой представленной балки имеется по два граничных условия. Это позволяет определять постоянные интегрирования С1 и С2 в решениях (а) и (б). Проследим применение метода непосредственного интегрирования для определения перемещений в конкретном случае.
Определить прогиб свободного конца балки с изгибной жесткостью EJx (рис. 9.5) методом непосредственного интегрирования дифференциального уравнения изогнутой оси балки. Решение. Решение основано на использовании дифференциального уравнения (9.4). Опорные реакции М 0= ql/2, Q 0= ql. Изгибающий момент в текущем сечении: М (z) = - М 0+ Q 0 z-qz 2/2=- ql 2/2+ qlz - qz 2/2 Подставим М (z) в уравнение (9.4) получим:
Проинтегрируем первый раз:
Второе интегрирование дает:
Граничные условия: при z= 0, v= 0, φ = 0. С их учетом получаем С 1= С 2=0. Прогиб свободного конца при z = l получаем:
Знак минус у прогиба vk показывает, что его направление противоположно положительному направлению оси у, а знак минус у угла поворота φк указывает на поворот сечения свободного конца балки по ходу часовой стрелки.
Пример № 9.2.
Решение. Ответы на поставленные вопросы дадим, используя уравнение (9.4). Изгибающий момент в сечении левого участка М I(z)= Аz=Рz/2, а в сечении правого участка изибающий момент M II(z) =Р (l-z) /2. Тогда дифференциальные уравнения на каждом участке балки будут иметь вид: Интегрируем дважды сначала уравнение (а), а потом уравнение (б) получаем:
Граничные условия: при z =0, vI =0; при z = l, vII= 0. Из второго уравнения следует, что D 1=0. Четвертое уравнение дает соотношение:
Воспользуемся условием симметрии балки и нагрузки. При z = l /2, φ I= 0. Тогда
Определим углы поворота сечений балки над опорами А и В. Используя уравнение (в) при z=0, получаем Приведенные примеры показывают, что применение метода непосредственного интегрирования ограничено на практике. Это связано с тем что при определении постоянных интегрировании приходится решать систему 2 n линейных алгебраических уравнений. На практике более широкое применение находят другие методы, основанные на использовании уравнения (9.4).
9.4. Метод начальных параметров определения перемещений при изгибе балок постоянной жесткости
Запишем для каждого участка балки дифференциальные уравнения (9.4). При действии указанной нагрузки ось балки изогнется. Определим прогибы и углы поворота сечений балки на каждом её участке. Для этого состаим на каждом из них дифференциальные уравнения:
Каждое из этих уравнений дважды проинтегрируем, не раскрывая скобки способом Клебша, получим:
Выразим постоянные интегрирования С и D через угол поворота φ0 и прогиб v 0 в начале координат балки, используя условие при z= 0, φ I =φ0, vI = v 0. В результате получаем C = EJx φ0, D = EJxv 0. А теперь учтем влияние распределенной нагрузки q на угол поворота φ и прогиб v в текущем сечении z балки (рис. 9.8). Воспользуемся способом замены переменной. На расстоянии η выделим элементарный отрезок балки d η в пределах которого распределенную нагрузку q можно считать постоянной. Влияние элементарной силы на угол поворота составит q η2 d η/2. Влияние всей распределенной нагрузки на угол поворота будет определяться интегралом:
Интеграл (ж) можно вычислить только при известной функции нагрузки q (z). При q = const интеграл (ж) принимает вид:
Аналогично можно показать влияние распределенной нагрузки на прогиб v в виде интеграла
Обобщая полученные результаты, формулы согласно методу начальных параметров для определения углов поворота и прогибов принимают вид:
Или
где m = z - am, p = z – ap, u н = z - a н, u к = z - a к
Знак Σ в уравнениях (9.5) и (9.6) означает, что учитываются несколько однотипных внешних нагрузок. Эти формулы могут быть использованы для определения прогибов и углов поворота в балках постоянной жесткости. В них содержатся статические начальные параметры М0, Q0, которые для статически определимых балок известны, либо могут быть найдены из условия равновесия. Кинематические начальные параметры φ0, v0 определяются из граничных условий, которые рассмотрены в п. 9.3. Рассмотрим некоторые примеры, иллюстрирующие применение уравнений метода начальных параметров по определению угловых и линейных перемещений в статически определимых балках.
Пример № 9.3.Для заданной статически определимой балки методом начальных параметров определитьуглы поворотаφ(z)ипрогибы v (z) на свободном краю консоли. 1. Сначала определим опорные реакции:
Проверим определение реакций опор:
2. Свяжем балку с системой координат zAy и сформулируем граничные условия: при z= 0, vI= 0; при z= 5м vII= 0. 3. Так как граничные условия сформулированы через функции прогибов v для первого и второго участков, то запишем уравнения прогибов для этих участков, используя формулу (9.6). а) Участок I
б) Участок II
4) Используя первое граничное условие из формулы (к) получаем: EJxv 0 = 0. По формуле (л) с использованием второго граничного условия получаем:
Откуда значение начального параметра: EJx φ0= -57,708/5 = -11,54 кНм2 5) Уравнения углов поворота и прогибов для третьего участка будут иметь вид:
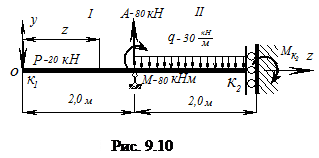
6) Подставляя координаты точки свободного конца консоли z = 7,5, м определим искомые перемещения
После вычислений получаем:
1.Определим опорную реакцию А из условия равновесия ∑ у =0, то есть -20-30·2+ А= 0, откуда А=80 кН. 2) Граничные условия: при z =2 м, vI =0; z =4 м, φII=0. 3) Записываем уравнение прогибов для первого участка и уравнение углов поворота для второго участка по формулам (9.5) и (9.6):
4. Подставим граничные условия в уравнения (а) и (б), получаем:
Откуда получаем: Так как точка к 1 совпадает с началом координат О выбранной системы осей zOy, то
Для определения прогиба в точке к 2 следует использовать уравнение прогибов для второго участка:
Таким образом, центр тяжести сечения, закрепленного вертикальным ползуном, переместится на величину:
Знак «минус» указывает на перемещение в отрицательном направлении оси у.
9.5. Энергетический метод определения перемещений в упругих системах
|
||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 440; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.111.9 (0.042 с.) |
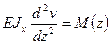 ;
; 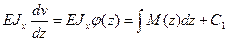 (а)
(а)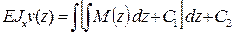 (б)
(б)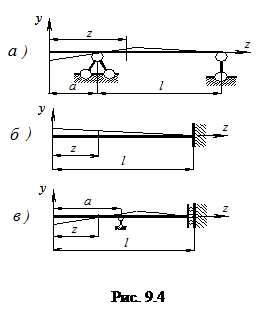 На рис. 9.4 показаны наиболее часто встречающиеся способы закрепления и связанные с ними граничные условия.
На рис. 9.4 показаны наиболее часто встречающиеся способы закрепления и связанные с ними граничные условия.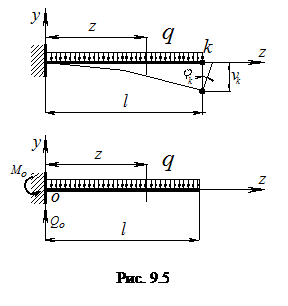 Пример № 9.1.
Пример № 9.1.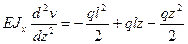
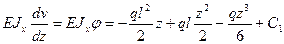
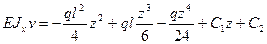

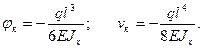
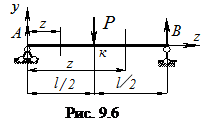 Определить прогиб v k в середине пролета балки постоянной жесткости EJx и углы поворота φ А и φ В опорных сечений (рис. 9.6) методом непосредственного интегрирования дифференциального уравнения (9.4).
Определить прогиб v k в середине пролета балки постоянной жесткости EJx и углы поворота φ А и φ В опорных сечений (рис. 9.6) методом непосредственного интегрирования дифференциального уравнения (9.4).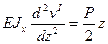 (а)
(а)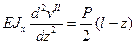 (б)
(б)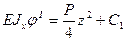
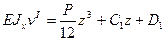
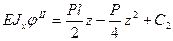
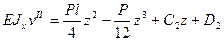
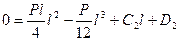 , или
, или 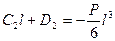
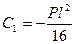 . Из условия симметрии балки при z = l /2, φ I= φ II получим:
. Из условия симметрии балки при z = l /2, φ I= φ II получим: 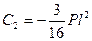 . Тогда значение постоянной интегрирования
. Тогда значение постоянной интегрирования 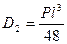 . Подставим значения постоянных интегрирования, получим уравнения углов поворота и прогибов на каждом участке балки в виде:
. Подставим значения постоянных интегрирования, получим уравнения углов поворота и прогибов на каждом участке балки в виде: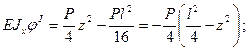 (в)
(в)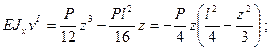 (г)
(г)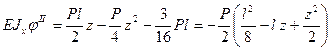 (д)
(д)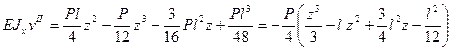 (е)
(е)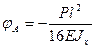 . По уравнению (д) при z = l находим
. По уравнению (д) при z = l находим 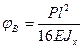 . Прогиб в середине пролета балки можно получить из уравнения (г), либо из уравнения (е) при z = l/2. Его значение составит:
. Прогиб в середине пролета балки можно получить из уравнения (г), либо из уравнения (е) при z = l/2. Его значение составит: 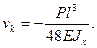
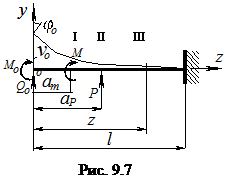 Рассмотрим консольную балку, загруженную системой сосредоточенных силовых факторов
Рассмотрим консольную балку, загруженную системой сосредоточенных силовых факторов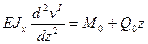
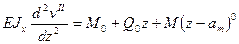
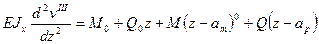
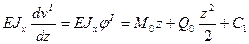 (а)
(а)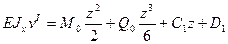 (б)
(б)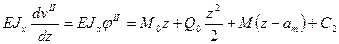 (в)
(в)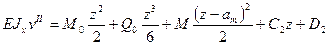 (г)
(г)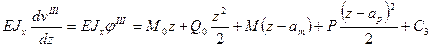 (д)
(д)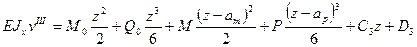 (е)
(е)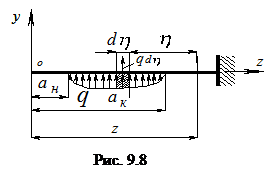 Найдем соотношения между постоянными интегрирования из условия непрерывности функций углов поворота и прогибов. Так при z=am углы поворота φ I =φ II и прогибы vI = vII. Сравнивая формулы (а) и (в) получаем С 1= С 2 и D 1= D 2. При z=am углы поворота φ II =φ III и прогибы vII = vШ путем сравнения (в) с (д), а также (г) с (е) получаем С 2= С 3 и D 2= D 3. А следовательно С 1= С 2= С 3= С и D 1= D 2= D 3= D. Таким образом независимых произвольных постоянный интегрирования осталось только две: С и D.
Найдем соотношения между постоянными интегрирования из условия непрерывности функций углов поворота и прогибов. Так при z=am углы поворота φ I =φ II и прогибы vI = vII. Сравнивая формулы (а) и (в) получаем С 1= С 2 и D 1= D 2. При z=am углы поворота φ II =φ III и прогибы vII = vШ путем сравнения (в) с (д), а также (г) с (е) получаем С 2= С 3 и D 2= D 3. А следовательно С 1= С 2= С 3= С и D 1= D 2= D 3= D. Таким образом независимых произвольных постоянный интегрирования осталось только две: С и D.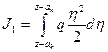 (ж)
(ж)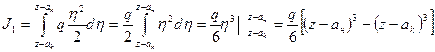 (з)
(з)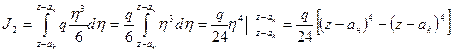 (и)
(и)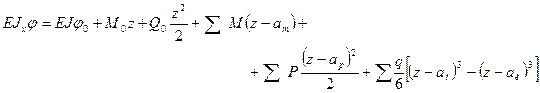 (9.5)
(9.5)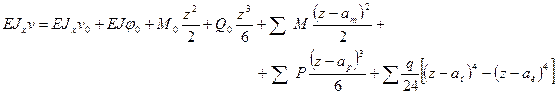 (9.6)
(9.6)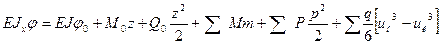 (9.5*)
(9.5*)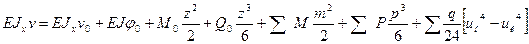 (9.6*)
(9.6*)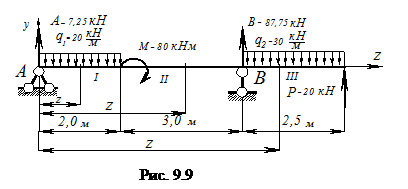
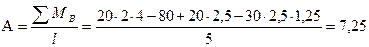 кН
кН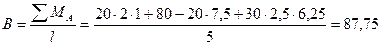 кН
кН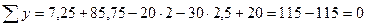 .
.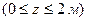 :
: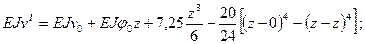 (к)
(к)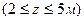 :
: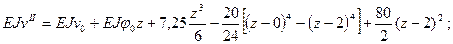 (л)
(л)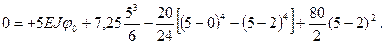
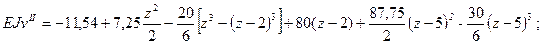
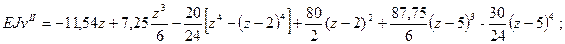
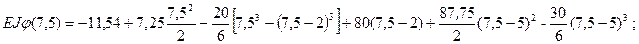
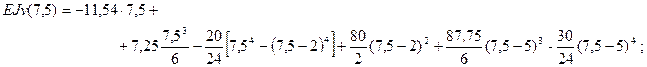
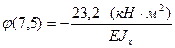 ;
; 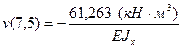 .
. Пример № 9.4.Для заданной статически определимой балки (рис.9.10) определитьугол поворотаφ в сечении к1 ипрогиб v в точках к1 и к2. Применить метод начальных параметров.
Пример № 9.4.Для заданной статически определимой балки (рис.9.10) определитьугол поворотаφ в сечении к1 ипрогиб v в точках к1 и к2. Применить метод начальных параметров.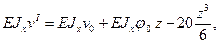 (а)
(а)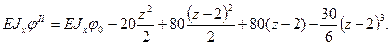 (б)
(б)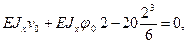
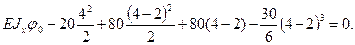
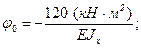
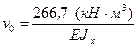 .
.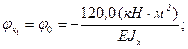
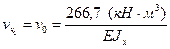 .
.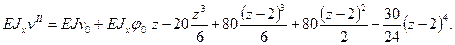
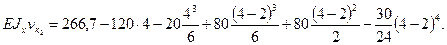
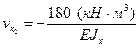 .
.


