
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кафедра теоретической и прикладной механикиСтр 1 из 26Следующая ⇒
ДОНБАССКАЯ НАЦИОНАЛЬНАЯ АКАДЕМИЯ СТРОИТЕЛЬСТВА И АРХИТЕКТУРЫ
Кафедра теоретической и прикладной механики Секция сопротивление материалов УДК 539.–3
РАСШИРЕННЫЙ ЭЛЕКТРОННЫЙ КОНСПЕКТ ЛЕКЦИЙ ПО КУРСУ «сопротивление материалов» для самостоятельной работы студентов в условиях кредитно-модульной системы с образовательно-квалификационным уровнем «БАКАЛАВР»
2 часть (весенний семестр)
направление подготовки 0921 «СТРОИТЕЛЬСТВО» для специальностей: 6.092100 «Промышленное и гражданское строительство», 6.092100 «Городское строительство и хозяйство», 6.092100 «Технология строительных конструкций изделий и материалов», 6.092100 «Строительство и эксплуатация автомобильных дорог и аэродромов», 6.092100 «Теплогазоснабжение и вентиляция», 6.092600 «Водоснабжение и водоотведение», 6.070800 «Экология».
АВТОРЫ: Профессор Мущанов В. Ф. Профессор Шевченко Ф. Л. Доцент Осыка В. И. Доцент Демидов А. И.
Макеевка 2006 г.
Содержание
Часть
МОДУЛЬ 9. ПЕРЕМЕЩЕНИЯ ПРИ ИЗГИБЕ БАЛОК. 3 9.1. Основные понятия. 3 9.2. Дифференциальное уравнение упруго-изогнутой оси балки. 4 9.3. Метод непосредственного интегрирования при определении перемещений в балках. Граничные условия. 5 9.4. Метод начальных параметров определения перемещений при изгибе балок постоянной жесткости 7 9.5. Энергетический метод определения перемещений в упругих системах. 13 9.6. Статически неопределимые балки. 22 Модуль 10. СЛОЖНОЕ СОПРОТИВЛЕНИЕ. 26 10.1. Общие понятия. 26 10.2. Сложный (неплоский) изгиб. 26 10.3. Изгиб с растяжением (сжатием) 32 10.4. Изгиб с кручением. Расчет круглого вала. 38 МОДУЛЬ 11. ПРОДОЛЬНО-ПОПЕРЕЧНЫЙ ИЗГИБ И УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ 40 11.1. Продольно-поперечный изгиб. 40 11.2. Устойчивость сжатых стержней. 41 11.3. Формула Эйлера. 42 11.4. Границы применимости формулы Эйлера. 46 11.5. Практический расчет сжатых стержней. 47 МОДУЛЬ 12. ДИНАМИЧЕСКОЕ ВОЗДЕЙТВИЕ НАГРУЗКИ.. 51 12.1. Учет сил инерции. 51 12.2. Приближенный динамический расчет упругих систем с распределенными параметрами 52 12.3. Собственные колебания упругих систем.. 53 12.4. Гармонические и ударные нагрузки при поперечных колебаниях. 55 12.5. Продольные колебания и удар. 57
МОДУЛЬ 13. РАСЧЕТ ТОНКОСТЕННЫХ ОБОЛОЧЕК. 59 13.1. Понятие о моментной и безмоментной теории расчета сосудов. 59 13.2. Расчет тонкостенных оболочек по безмоментной теории. 60 13.3. Частные случаи напряженного состояния оболочек. 62 Модуль 14. ПОНЯТИЕ О КОНЦЕНТРАЦИИ НАПРЯЖЕНИЙ.. 66 14.1. Общие понятия о концентрации напряжений. 66 14.2 Проверка прочности с учетом местных напряжений. 68 МОДУЛЬ 15. Колебания упругих систем.. 72 15.1. Колебания систем с одной степенью свободы.. 72 15.2. Собственные незатухающие колебания. 74 15.3. Собственные затухающие колебания. 78 15.4. Вынужденные колебания без учета сопротивления движению.. 79 15.5. Ударные нагрузки. 81 15.6. Вынужденные колебания при гармонических нагрузках. 83 15.7. Колебания систем с двумя степенями свободы.. 85 15.8. Поперечные колебания систем с распределенными параметрами. 87 15.9. Собственные колебания весомых балок. 88 15.10. Вычисление спектра частот собственных колебаний. 89 15.11. Метод начальных параметров в колебаниях балок. 90 15.12. Учет сосредоточенных масс в колебаниях весомых балок. 91 15.13. Учет гармонической нагрузки в весомых балках. 93 ЛИТЕРАТУРА. 95 МОДУЛЬ 9. ПЕРЕМЕЩЕНИЯ ПРИ ИЗГИБЕ БАЛОК Основные понятия
Однако этого недостаточно, чтобы дать полную оценку работы балок под нагрузкой. Балки должны удовлетворять не только условиям прочности, но и условиям жесткости, т.е. при действии на них внешних нагрузок они должны не допускать чрезмерных перемещений. При расчете строительных конструкций допустимые перемещения регламентируются строительными нормами на проектирование. Таким образом, чтобы выполнить расчеты на жесткость следует научиться определять перемещения, возникающие в балках. Кроме того, как известно, при раскрытии статической неопределимости систем составляются дополнительные уравнения, связывающие между собой перемещения. Следовательно, возникает вторая необходимость определения перемещений.
Какие же перемещения возникают в балках? Какая взаимосвязь существует между ними? Какие зависимости существуют между перемещениями и внутренними усилиями. Каким образом их определить? В дальнейшем нам с вами предстоит ответить на все поставленные здесь вопросы. Рассмотрим некоторую балку в виде консоли, загруженную силой Р (рис.9.1), связанную с системой координатных осей zoy. При действии этой силы продольная ось балки изогнется, т.е. центры тяжести сечения переместятся на величину u по направлению оси z и на величину v по направлению оси y, а поперечные сечения повернутся на угол φ. Но составляющая u полного перемещения обычно значительно меньше вертикальной составляющей v, в дальнейшем называемой прогибом в балке. Поэтому составляющей u можно пренебречь и считать, что все точки оси балки перемещаются только по вертикали. Таким образом, при изгибе балки будем задачи решать относительно двух функций – прогиба v (z) и углов поворота сечений φ(z) в балке, между которыми имеет место дифференциальная зависимость:
Существует несколько методов определения указанных перемещений. В дальнейшем остановимся на некоторых из них. Прежде всего, обратим внимание на метод непосредственного интегрирования дифференциального уравнения изогнутой оси балки.
Общие понятия
Под сложным сопротивлением обычно понимают различные комбинации уже известных нам простых видов загружений (растяжения-сжатия, изгиба, кручения и т.д.), в результате чего в поперечном сечении элемента одновременно действует несколько силовых факторов. Использование принципа независимости действия сил, позволяет получить для этого случая результирующие напряжения, перемещения, определяемые путем суммирования напряжений, перемещений, возникающих от внутренних усилий (N, Qx, Qy, Mкр, Mx, My), соответствующих простым деформациям растяжения (сжатия), сдвига, кручения, изгиба, возникающих при загружении стержня произвольной нагрузкой. Следует заметить, что подобный подход, основанный на использовании принципа суперпозиции применим при рассмотрении достаточно жестких стержней, для которых справедливы линейные зависимости между деформациями и напряжениями Наиболее распространенными комбинациями сложного сопротивления являются косой (неплоский) изгиб, изгиб с растяжением (сжатием), внецентренное растяжение (сжатие), изгиб с кручением, которые мы и рассмотрим ниже.
Сложный (неплоский) изгиб
Сложный или неплоский изгиб возникает в том случае, когда равнодействующая внешних сил (т.е. результат действия внешних сил, располагающихся в различных плоскостях и проходящих через продольную ось балки), действует под углом к главным осям инерции сечения (рис. 10.1. а). В отличие от плоского изгиба, изогнутая ось балки в этом случае является не плоской кривой.
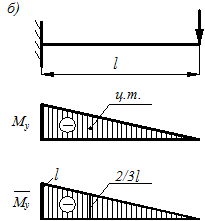
Частным случаем сложного изгиба является косой изгиб (рис. 10.1 б), при котором все нагрузки, вызывающие изгиб, действуют в одной плоскости, не совпадающей ни с одной из главных плоскостей. Примером конструкций, подвергающихся косому изгибу, могут служить кровельные прогоны (обрешетка кровли), когда вертикальная нагрузка от веса кровли и собственного веса прогона действует под углом к главной оси сечения.
Так же косой изгиб могут испытывать несимметричные сечения. В качестве примера может служить балочный элемент, выполненный из уголкового профиля, у которого одна из полок расположена параллельно основанию. Поскольку для него вертикальная нагрузка от собственного веса будет действовать под углом к главным осям инерции сечения, то этот элемент также будет испытывать косой изгиб. Использование указанных выше общих гипотез позволяет рассмотреть сложный (косой) изгиб как сумму двух плоских изгибов, действующих в плоскостях zoy и zox. В связи с этим нагрузки, действующие в произвольных плоскостях, раскладываются на две составляющие, лежащие в главных плоскостях zoy и zox (рис. 10.3) Px = P cos φ, Py = P sin φ Возникающие в поперечном сечении стержня соответствующие изгибающие моменты Mx = Py · z = P · z sin φ My = P · z cos φ действуют одновременно и вызывают в произвольной точке любого сечения результирующие напряжения (см. рис.10.2 а). σz = Примечание: за положительные принимаются изгибающие моменты Mx и My, вызывающие растяжение в любой точке, располагающейся в 1-м квадранте системы координат xoy (рис. 10.2 а). Обозначим соотношение величин изгибающих моментов Mx и My, возникающих в сечении, через ctg φ ctg φ =
При этом следует четко различать определения, часто используемые при рассмотрении данного раздела, а именно: - силовой линии - след плоскости действия нагрузки при косом изгибе на поперечном сечении стержня; - нейтральной линии- геометрическое место точек, в которых действующие напряжения σz=0. Поскольку результатом действия обоих внутренних усилий Mx и My являются нормальные напряжения σz, появляется возможность суммировать эти величины σ = Для точек, находящихся на нейтральной линии, нормальные напряжения σ, вычисляемые по формуле (10.3) будут равны нулю. Но, так как по условию задачи
Положение нейтральной линии определяется тангенсом угла наклона этой прямой, проходящей через начало осей координат (рис. 10.2 б). Разрешив уравнение (10.4) относительно отношения yн/xн (здесь yн и xн – координаты точки, лежащей на нейтральной оси), получим
tg β = tg β = Из рис. 10.3 видно, что tg β = ctg γ. Так как углы φ и γ откладываются от взаимно перпендикулярных осей х и у, то равными они могут быть лишь при выполнении условия Ix = Iy. Анализируя выражение (10.5) и приведенное утверждение можно прийти к 2-м важным выводам: 1. В общем случае при Ix ≠ Iy β + φ ≠ 900,то есть силовая линия и нейтральная линия не ортогональны. 2. Так как при косом изгибе отношение My / Mx = ctg φ постоянно по всей длине стержня, то и угол наклона нейтральной линии β также постоянен по всей длине стержня, а упругая линия деформированного стержня располагается в одной плоскости – плоскости изгиба. Проверка прочности при сложном (косом) изгибе осуществляется на основе использования формулы (10.1). При этом максимальные напряжения возникают в точках А и С, наиболее удаленных от нейтральной линии (рис. 10.3, где эпюры σz(Mx) и σz(My) построены по граням сечения).
где Wx = Ix / yA = Ix / yC, Wy = Iy / xA = Iy / xC, - максимальные значения моментов сопротивления сечения, вычисленные для наиболее растянутой (А) и наиболее сжатой (С) точек сечения, вычисленные относительно главных осей сечения х и у соответственно. Перемещения, как и напряжения, определяются на основе использования принципа независимости действия сил. В любом сечении величина полного прогиба определяется суммированием его проекций δ = где δx и δy – проекции полного прогиба d, определяемые на основе использования методов теории перемещения.
Направление полного перемещения найдем из рассмотрения примера №1 (рис. 10.4), где перемещения определяются на основе использования правила Верещагина. Пример №10.1. Определить полное перемещение точки В от илы Р, приложенной под углом к горизонтали. Разложим силу Р на две составляющих в вертикальной горизонтальной плоскости. Построив соответствующие грузовые и единичные эпюры, найдем перемещения по вертикали и горизонтали.
Если принять во внимание, что tg α·tg β = то α + β = 900 (рис.10.3). Следовательно, нейтральная линия и направление перемещения ортогональны, а направление действия нагрузки не совпадает с направлением перемещения, что является весьма важной особенностью и определяет само название явления - косой изгиб.
Рис. 10.4.
Продольно-поперечный изгиб
Из самого названия напряженно-деформированного состояния следует, что стержень загружен не только поперечной, но и продольной нагрузкой, рис. 11.1.
Следовательно, продольно-поперечный изгиб – это вид деформации, когда на стержень одновременно действует продольная и поперечная нагрузка. Поперечная нагрузка вызывает изгиб стержня, а продольная – в основном сжатие. Можно ли в этом случае вычислять напряжения по принципу суперпозиции
В случае весьма жестких стержней напряжения, вычисленные по формуле (11.1), будут достаточно достоверными, но в случае гибких стержней (с небольшой изгибной жестокостью) применение формулы (11.1) приведет к большой погрешности. Принцип суперпозиции при продольно-поперечном изгибе не применим, так как продольная сила Для вычисления действительных напряжений дополнительный изгибающий момент нужно вычислять с учетам действительных прогибов, вызванных одновременный воздействием как поперечной так и продольной нагрузок. Задача сводится к вычислению этих перемещений, т.е. к определению уравнения изогнутой оси стержня. Наиболее эффективно при этом использовать метод начальных параметров. Рассмотрим балку под действием продольной силы
Обозначив через
получим
Решение этого уравнения представим в виде
Разыскивая частное решение y * в виде полинома y *= a + bz и подставляя его в исходное уравнение (11.3), способом неопределенных коэффициентов находим
При этом уравнение (11.3) примет следующий вид
Отсюда дифференцированием можно получить уравнение углов поворота
Выразим постоянные интегрирования А и В через начальные параметры из условий, что при z =0, y = y 0,
Если бы к балке была приложена только сила P 0, то уравнение изогнутой оси (11.3) имело бы вид
В случае загружения балки лишь одним моментом M 0
Здесь Отсюда следует, что к поперечной нагрузке можно применять принцип суперпозиции, но при каждом загружении нужно учитывать продольную силу. Формула Эйлера
Для вывода формулы критической силы (формулы Эйлера) рассматривается сжатый стержень в безразличном слегка изогнутом состоянии. Безразличное состояние равновесия стержня, возникающее при критической силе – это такое состояние, когда сжатый стержень может сохранять прямолинейную недеформированную или слегка изогнутую форму. Используем приближенное дифференциальное уравнение изогнутой оси стержня Однако этот процесс можно сократить, если использовать уже подготовленное уравнение изогнутой оси стержня в начальных параметрах. Остается лишь подчинить это уравнение условиям закрепления стержня на опорах. Это условия, отвечающие определенным известным значениям силовых или деформационных параметров на концах стержня. Из этих условий можно получить систему однородных уравнений, определитель которой приравнивается нулю. Такая система уравнений, описывающих условия закрепления стержня на опорах, однородная, т.е. правая часть равна нулю. В тривиальном решении неизвестные силовые и деформационные факторы будут равны нулю, что не отвечает потере устойчивости, т.е. потере первоначальной прямолинейной формы равновесия. Чтобы получить ненулевое решение нужно главный определитель приравнять нулю. При этом числитель и знаменатель при определении неизвестных параметров будут равны нулю, что дает неопределенное, но ненулевое решение. Такой определитель приводится к трансцендентному уравнению. Трансцендентное уравнение имеет вид уравнения не представляющего алгебраические функции из букв и цифр, связанных алгебраическими действиями. Собственные числа этого уравнения позволяют найти параметр k, а затем по (11.2) найти критическую силу Собственные числа - это корни трансцендентного уравнения, при которых функция принимает нулевое значение.
Согласно (11.6) уравнение изогнутой оси стержня принимает вид
В этом уравнении остается один неизвестный начальный параметр θ0 (кроме уже использованных), соответственно чему осталось одно граничное условие при z = l y =0.Обратим внимание на то, что здесь нельзя брать условие симметрии изогнутого стержня, так как при этом останутся неучтенными кососимметричные формы изгиба стержня. Таким образом, из условия шарнирного закрепления стержня на правой опоре находим, что
и уравнение изогнутой оси
При n =1 получаем наименьшее значение критической силы
которой соответствует изгиб стержня по синусоиде с одной полуволной (рис. 11.2). При n =2 критическая сила в четыре раза больше первой, а стержень изгибается по синусоиде с двумя полуволнами. Так можно получить бесконечное множество критических состояний. Но изгиб стержня по синусоиде с n -ным количеством полуволн (минуя предшествующие) может произойти при особах условиях загружения (например, при воздействии взрывной волны), а при статическом нагружении каждой последовательно возрастающей критической силе соответствует n -ное и (n -1)-е состояние равновесия. Так, при первой критической силе возможны прямолинейная форма равновесия и форма изгиба по одной полуволне. Поскольку при незначительном превышении критической силы происходит стремительное возрастание прогибов, когда возникают большие изгибные напряжения, то в инженерной практике для сжатых стержней критическую силу (даже первую) допускать нельзя. Поэтому за критическую принимают первую наименьшую силу, которую считают разрушающей. По этой силе устанавливается пас устойчивости сжатого стержня.
Поскольку в этом уравнении два неизвестных параметра y 0 и θ0, то нужно рассмотреть два условия при z = l y = θ = 0. Из этих условий получим два однородных уравнения:
Чтобы иметь ненулевые значения начальных параметров y 0 и θ0 , определитель этой системы приравниваем нулю. Отсюда получаем
По уравнению изогнутой оси из условия z = l y =0 находим Здесь и дальше ограничимся только первой критической силой и ей соответствующего уравнения изогнутой оси. Если на верхнем конце стержня установить шарнирную опору (рис. 11.3 б), то согласно 11.6 получим:
Здесь наличие реакции А очевидно из суммы моментов всех сил относительно заделки, где возникает опорный момент, а направление ее может быть какое угодно (как влево, так и вправо). Из условия защемления на нижнем конце стержня при z = l y =θ=0 получаем систему уравнений
определитель которой приравниваем нулю:
Отсюда получаем трансцендентное уравнение
На основании уравнения изогнутой оси стержня (11.9) из условия, при z = l y =0, можно выразить θ0 через А. Тогда уравнение изогнутой оси стержня (11.9) примет следующий вид: Положение сечения с наибольшим прогибом найдем, приравнивая угол поворота Рассмотрим стержень, жестко защемленный с двух сторон (рис. 11.3 в), при чем верхняя заделка является вертикально подвижной. Согласно (11.6) получаем:
Из условия при z = l y =θ=0 получаем систему однородных уравнений, определитель которой приравниваем нулю:
Отсюда получаем трансцендентное уравнение
Все формулы критической силы при различных условиях закрепления можно представить в виде
где μ – коэффициент приведения длины, указывающий, какая часть действительной длины стержня изгибается по синусоиде с одной полуволной аналогично основному случаю (рис.11.2). Поскольку
Знаменатель этой формулы для каждого конкретного случая находится из трансцендентного уравнения. Если это уравнение дает несколько корней, то для вычисления наименьшей критической силы нужно брать наименьший корень kl, чтобы коэффициент приведения длины (11.13) был наибольшим, а критическая сила наименьшей. Один из корней уравнения (11.12) получим, положив
На основании уравнения изогнутой оси (11.12) из условия защемления, т.е. при z = l y =0, можно выразить М 0 через А, и тогда уравнение изогнутой оси стержня примет следующий вид
Вторая критическая сила с коэффициентом приведения длины μ=0,35 соответствует кососимметричной форме изгиба и проявляется она после первой формы, что практического значения не имеет. В случае свободно смещающейся заделки (рис. 11.4 г) уравнения изогнутой оси и углов поворота имеют следующий вид:
Из условий
Учет сил инерции
В предыдущих разделах рассматривались расчеты элементов конструкций на статическую нагрузку, которая во времени не изменяется или медленно возрастает от нулевого до окончательного значения. Динамической считается нагрузка, изменяющаяся во времени с переменной скоростью или приложенная за короткое время, в том числе и внезапно. Такая нагрузка вызывает ускорения элементов конструкций, в связи с чем появляются силы инерции, которые по принципу Даламбера нужно учитывать вместе с нагрузкой статической в виде произведения массы М на ускорение а
Частным случаем такой нагрузки является вес конструкции или сосредоточенных масс, когда произведение массы М на ускорение земного притяжения g считается весовой статической нагрузкой
Простейшим случаем динамической нагрузки является сила инерции массы, движущейся с постоянным известным ускорением. В этом случае сила инерции направляется в сторону обратную ускорению и задача решается в квазистатике (как бы в статике) с учетом статического загружения и силы инерции. Простейшим случаем динамического воздействия нагрузки может быть подъем сосредоточенной массы М на невесомом канате с известным ускорением а. Здесь нужно кроме веса груза Q = Mg учитывать силу инерции движущегося вверх груза Pи = Ma ирасчетное усилие в канате будет равно Nд = M g+ Ma = Mg (1+ a/g)= Qkд, т.е. расчет можно производить на статическую нагрузку Q с учетом динамического коэффициента kд= 1+ a /g. Этот же коэффициент будет учитываться при вычислении напряжений σ д =σст kд и перемещений
Решение. Сила инерции элемента кольца ds = rd φ направлена перпендикулярно оси вращения и равна dp = mds · a = mrd φ·θ2 r sinφ. Эта динамическая нагрузка изменяется от нулевого значения на оси вращения до максимального на горизонтальной оси, проходящей через центр тяжести кольца, но интенсивность сил инерции на вертикальную проекцию элемента ds sinφ = = rd φ·sinφ будет постоянной и равной p = m θ2 r. Таким образом, кольцо нужно рассчитывать на равномерно распределенную нагрузку интенсивностью p. Кольцо представляет трижды cтатически неопределимую систему, но с учетом симметрии конструкции и симметричного изгиба кольца относительно вертикальной и горизонтальной оси, где изгибающие моменты экстремальные, следует, что в диаметральных сечениях поперечные силы равны нулю. С учетом этого, рассматривая в равновесии четверть кольца, находим, что в горизонтальном сечении продольное усилие равно нулю, а в вертикальном N = pr. Чтобы вычислить изгибающий момент в горизонтальном сечении M 0= X 1 методом сил, основную систему можно принять в виде четверти кольца с защемленем в вертикальном сечении, так как это сечение не поворачивается, а только смещается по вертикали. Для вычисления главного коэффициента канонического уравнения метода сил δ11 X 1+Δ1p=0 положим X 1=1. Тогда Таким образом, кольцо нужно рассчитывать из условия его прочности в вертикальном сечении, где
Продольные колебания и удар
В приближенных расчётах при продольных колебаниях и ударе распределенная масса стержня также заменяется сосредоточенной, вычисленной по (11.1), (11.2). После этого производится расчет одномассовой системы.
Решение. Заменим распределенную массу m сосредоточенной, приведенной к нижнему концу стержня (рис. 12.9). В качестве приближенного уравнения перемещений сечений стержня примем
Приведенная масса будет такой:
Так как
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 97; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.254.35 (0.142 с.) |
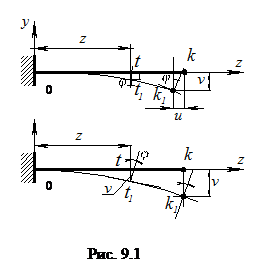 Ранее были рассмотрены вопросы, связанные с исследованием напряженного состояния балок при действии на неё внешних нагрузок. При этом основное внимание было уделено рассмотрению условий, при которых обеспечивается несущая способность балок.
Ранее были рассмотрены вопросы, связанные с исследованием напряженного состояния балок при действии на неё внешних нагрузок. При этом основное внимание было уделено рассмотрению условий, при которых обеспечивается несущая способность балок.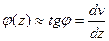 (9.1)
(9.1)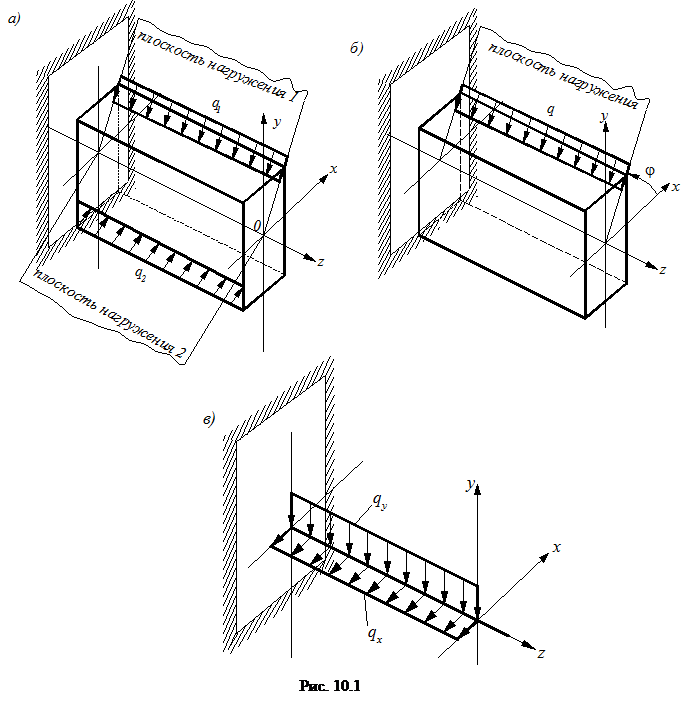
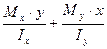 (10.1)
(10.1)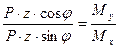 (10.2)
(10.2)
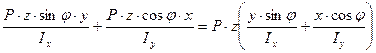 (10.3)
(10.3)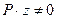 , то нулю для выполнения этого условия нулю должно равняться выражение в скобках, то есть
, то нулю для выполнения этого условия нулю должно равняться выражение в скобках, то есть = 0 (10.4)
= 0 (10.4)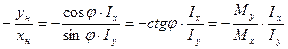
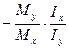 - уравнение нейтральной линии (10.5)
- уравнение нейтральной линии (10.5)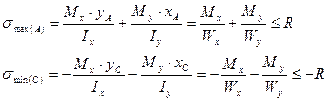 (10.6)
(10.6)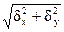 (10.7)
(10.7)
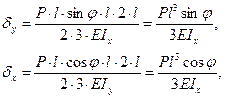 (10.8)
(10.8) (10.9)
(10.9) ,
,


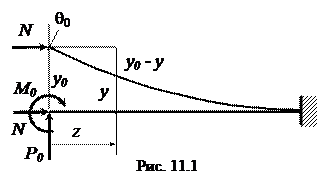
 (11.1)
(11.1)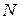 в изогнутом стержне вызывает дополнительный изгиб Принцип суперпозиции – принцип независимости и сложения действия сил, заключающийся в том, что силовые фактор, напряжения и перемещения, т.е. все, кроме работы и потенциальной энергии, можно вычислять от каждой нагрузки отдельно и результаты складывать.
в изогнутом стержне вызывает дополнительный изгиб Принцип суперпозиции – принцип независимости и сложения действия сил, заключающийся в том, что силовые фактор, напряжения и перемещения, т.е. все, кроме работы и потенциальной энергии, можно вычислять от каждой нагрузки отдельно и результаты складывать.
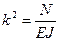 (11.2)
(11.2)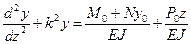 (11.3)
(11.3)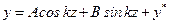
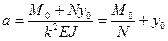 ,
, 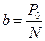 .
.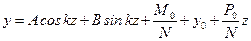 (11.4)
(11.4)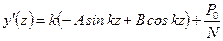 , (11.5)
, (11.5)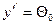 . Из этих условий находим
. Из этих условий находим 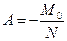 ,
, 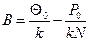 или
или 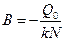 . Подставляя в уравнение (11.5) постоянные А и В, получим
. Подставляя в уравнение (11.5) постоянные А и В, получим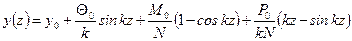 . (11.6)
. (11.6)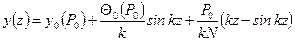 .
.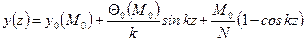 .
.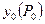 ,
, 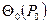 ,
, 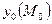 ,
, 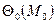 - начальные параметры при отдельном загружении балки нагрузками
- начальные параметры при отдельном загружении балки нагрузками 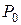 и
и 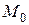 соответственно.
соответственно.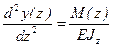 , а его решение подчиним условиям закрепления стержня на опорах.
, а его решение подчиним условиям закрепления стержня на опорах.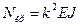 .
.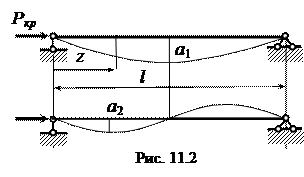 Рассмотрим простейший случай стержня шарнирно закрепленного на опорах (основной случай), рис. 11.2. В этом случае на опоре (при z =0)
Рассмотрим простейший случай стержня шарнирно закрепленного на опорах (основной случай), рис. 11.2. В этом случае на опоре (при z =0) 
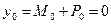 .
.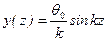 .
.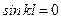 . Это значит, что
. Это значит, что  , а, следовательно, из (11.2) найдем критическую силу
, а, следовательно, из (11.2) найдем критическую силу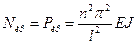 , n = 1, 2, 3,
, n = 1, 2, 3, 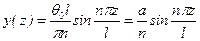 .
.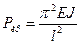 , (11.7)
, (11.7)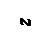
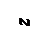
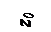
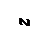
 Если стержень жестко защемлен с одной стороны, а с другой свободный (рис.11.3, а), то при выборе начала координат на свободнном конце стержня
Если стержень жестко защемлен с одной стороны, а с другой свободный (рис.11.3, а), то при выборе начала координат на свободнном конце стержня  . Следовательно, согласно (11.6) получим
. Следовательно, согласно (11.6) получим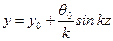 .
.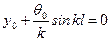 ,
,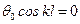 .
.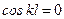 , т.е.
, т.е. 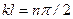 , n =1, 3, … Следовательно, критическая сила и уравнение изогнутой оси стержня будут следующими:
, n =1, 3, … Следовательно, критическая сила и уравнение изогнутой оси стержня будут следующими: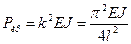 , (11.8)
, (11.8)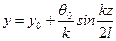 .
.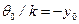 , Следовательно,
, Следовательно, 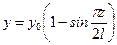 , что соответствует форме изгиба, показанной на рис. 11.3 а.
, что соответствует форме изгиба, показанной на рис. 11.3 а.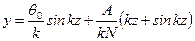 , (11.9)
, (11.9)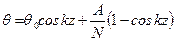 .
.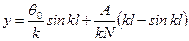 , (11.10)
, (11.10)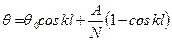 ,
,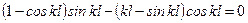 .
.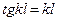 , откуда находим первый корень
, откуда находим первый корень 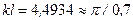 . Значит, согласно (11.2)
. Значит, согласно (11.2)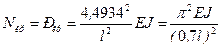 . (11.11)
. (11.11)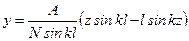 .
.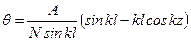 нулю. Из этих условий найдем
нулю. Из этих условий найдем 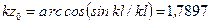 , т.е. z 0=0,3983 l. В этом сечении возникает прогиб
, т.е. z 0=0,3983 l. В этом сечении возникает прогиб  . Точка перегиба на изогнутой оси будет там, где кривизна
. Точка перегиба на изогнутой оси будет там, где кривизна 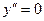 , т.е. при
, т.е. при 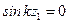 . Отсюда находим длину участка стержня до точки перегиба z 1 =0,7 l.
. Отсюда находим длину участка стержня до точки перегиба z 1 =0,7 l.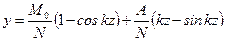 , (11.12)
, (11.12)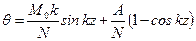 .
.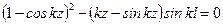 .
.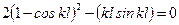 или
или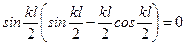 . (11.13)
. (11.13)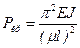 , (11.14)
, (11.14)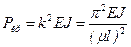 , то коэффициент приведения длины можно находить по формуле
, то коэффициент приведения длины можно находить по формуле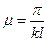 . (11.15)
. (11.15)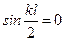 , что соответствует значению
, что соответствует значению 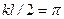 . Второй корень найдем, положив
. Второй корень найдем, положив  , откуда находим
, откуда находим 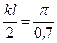 . По меньшему значению корня kl =2π определяем коэффициент приведения длины μ=0,5, чему соответствует критическая сила
. По меньшему значению корня kl =2π определяем коэффициент приведения длины μ=0,5, чему соответствует критическая сила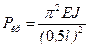 . (11.16)
. (11.16)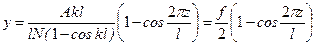 .
.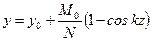 ,
, 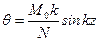 .
.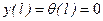 получим kl =π, т.е. μ=1. Критическая сила такая же, как в основном случае.
получим kl =π, т.е. μ=1. Критическая сила такая же, как в основном случае.
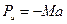 . (12.1)
. (12.1) . (12.2)
. (12.2) , где: l – длина каната с жесткостью EF.
, где: l – длина каната с жесткостью EF.
 Пример 12.1. Тонкостенное кольцо с известной погонной массой m вращается вокруг вертикальной оси с заданной угловой скоростью θ, рис. 12.1. Найти, расчетные напряжения.
Пример 12.1. Тонкостенное кольцо с известной погонной массой m вращается вокруг вертикальной оси с заданной угловой скоростью θ, рис. 12.1. Найти, расчетные напряжения.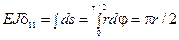 . Грузовой коэффициент
. Грузовой коэффициент 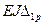
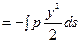 . Поскольку y = r cosφ, а ds = rd φ, то
. Поскольку y = r cosφ, а ds = rd φ, то 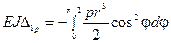
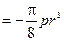 . Значит,
. Значит, 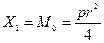 . Изгибающий момент в произвольном сечении
. Изгибающий момент в произвольном сечении 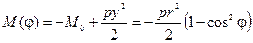 , а в вертикальном сечении
, а в вертикальном сечении  .
. .
. 
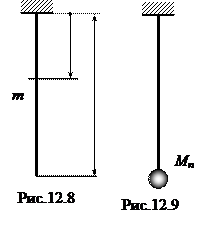 Пример 12.7.Найти приближенно частоту первого тона продольных колебаний весомого стержня (рис. 12.8).
Пример 12.7.Найти приближенно частоту первого тона продольных колебаний весомого стержня (рис. 12.8).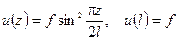 .
.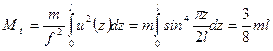 .
.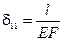 , то приближённое значение частоты основного тона колебаний:
, то приближённое значение частоты основного тона колебаний: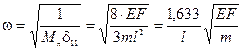 - это на 3,96% больше точного значения, равного
- это на 3,96% больше точного значения, равного  .
.


