
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрический смысл дифференциала функции
Дифференциал функции y = f(x) в точке x равен приращению ординаты касательной к графику функции в точке M(x, f(x)), когда аргумент x получит приращение Δx.
2.4.2.
Свойство 1. Дифференциал постоянной равен нулю: dc = 0. Действительно: dc = c'dx = 0∙dx = 0. Свойство 2. Постоянное число можно выносить за знак дифференциала: d(cu) = cdu. Действительно: d(cu) = (cu)'dx = c∙u'dx = c d u. Свойство 3. Дифференциал суммы дифференцируемых функций равен сумме дифференциалов: d(u + v) = du + dv. Действительно, d(u + v) = (u + v)'dx = u'dx + v'dx = du + dv. Свойство 4. Дифференциал произведения дифференцируемых функций находится по формуле: d(uv) = udv + vdu. Свойство 5. Дифференциал частного дифференцируемых функций находится по формуле: d æ u ö = vdu - udv
(v ¹ 0). ç v ÷ v 2 è ø Свойство 6. Инвариантность формы дифференциала. Рассмотрим дифференцируемые функции u = u(x), y = f(u). Тогда дифференциал сложной функции y = f(u(x)) находится по формуле: dy = f '(u)du. Если сравним последнюю формулу с определением дифференциала, то получим, что дифференциал имеет неизменную (инвариантную) форму относительно аргумента. Действительно, по формуле производной сложной функции имеем: dy = (f(u(x)))'dx = f '(u) ∙u'(x)dx = f '(u)du, т.к. du = u'(x)dx.
Решение. d (sin x) = d sin u = cos u × du = cos × d x, гдеu = x.
Таблица дифференциалов основных элементарных функций. 1. d (xa)= axa -1 dx. 2. d (a x) = a x ln a × dx, d (ex) = exdx.
3. d (log a x) = 1
x ln a
dx, d (ln x) = dx.
4. d (sin x) = cos xdx. 5. d (cos x) = -sin xdx. 6. dx. cos2 x 7. dx. sin 2 x 8. при x < 1.
9.
d (arccos x) = -
d (arctgx) = dx
при x < 1.
1 + x 2 11. d (arcctgx) = - dx.
ОДНОЙ ПЕРЕМЕННОЙ. Основные теоремы дифференциального исчисления и их геометрическая иллюстрация. Правило Лопиталя. 2.5.1. Теорема Ферма, еѐ геометрический смысл. 2.5.2. Теорема Роля,, еѐ геометрический смысл. 2.5.3. Теорема Лагранжа, еѐ геометрический смысл. 2.5.4. Правило Лопиталя.
2.5.1.
Теорема Ферма. Пусть функция y=f(x) определена на отрезке [ a,b ] и в некоторой точке с, лежащей между точками а и b, (а < с < b), принимает свое наибольшее или наименьшее значение. Если в точке с существует производная, то она равна нулю: f '(c)=0.
Доказательство. Пусть для определенности в точке c функция f (x)
принимает наибольшее значение, т.е. f (x) £ f (c) для всех a £ x £ b. Тогда приращение функции D y = f (c + D x) - f (c) £ 0. Отсюда следует, что D y £ 0
при D x > 0, D y ³ 0
при D x < 0. По определению производной f ¢(c) = lim D y £ 0
при D x D x > 0,
f ¢(c) =
lim D y ³ 0
при
D x < 0. Следовательно,
f ¢(c) = 0. D x ®0 D x D x ®0 D x
|
|||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 243; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.54.63 (0.012 с.) |
 Основные свойства дифференциалов. Таблица дифференциалов основных элементарных функций. Применение в приближенных вычислениях.
Основные свойства дифференциалов. Таблица дифференциалов основных элементарных функций. Применение в приближенных вычислениях.


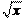
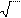 Пример. Найти дифференциал сложной функции
Пример. Найти дифференциал сложной функции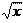
 y = sin .
y = sin .
 x
x d (tgx) =
d (tgx) =

 d (ctgx) = -
d (ctgx) = - d (arcsin x) = dx
d (arcsin x) = dx
 10.
10.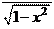 dx.
dx.
 1 + x 2
1 + x 2 ТЕМА 2. 5. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ
ТЕМА 2. 5. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ Теорема Ферма, еѐ геометрический смысл.
Теорема Ферма, еѐ геометрический смысл. D x
D x



