
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Однако все сформулированные теоремы о производных первых порядков выполняются для производных высших порядков.
2. Геометрический смысл производной. Определение. Угловой коэффициент касательной, проведённой к графику функции y = f(x) в точке Уравнение этой касательной имеет вид:
Пример. Составить уравнение касательной к графику функции Найдём
Уравнение касательной будет иметь вид:
3. Физический смысл производной. Мгновенная скорость прямолинейного движения материальной точки в любой момент времени t есть производная от пути s по времени t.
Вторая производная пути s по времени t равна ускорению движения тела в данный момент времени.
Пример. Закон движения точки по прямой задан формулой Найти скорость и ускорение движения точки в конце первой секунды. Решение: Т.к. V(t) = S`(t), то
Т.к. а(t) = V`(t), то 4. Приложения производной к исследованию функции. Возрастание и убывание функции Определение. Функция Определение. Функция Интервалы возрастания и убывания функции называются интервалами монотонности функции. Справедлива следующая теорема. Теорема (необходимое и достаточное условия возрастания (убывания) функции). Пусть функция 1) если функция
2) если производная 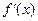 на интервале на интервале 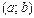 положительна (отрицательна), т.е. положительна (отрицательна), т.е. 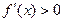 , , 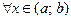 ( (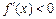 , , 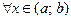 ), то функция ), то функция 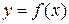 на на 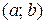 возрастает (убывает). возрастает (убывает).
Пример. Найти промежутки возрастания и убывания функции y = 4x3 – 5x2 + 2. Найдем производную функции Решим неравенство
+ - +
0 Таким образом, функция возрастает при Решая неравенство Экстремумы функции Пусть функция
Определение. Точка Определение. Точка Определение. Точки минимума и максимума функции называются ее точками экстремума. Для функции, дифференцируемой в точке
Определение. Точки, в которых производная функции Очевидно, что не любая стационарная точка функции является ее точкой экстремума. Например, функция Теорема. (первое достаточное условие экстремума функции). Пусть Замечание. Из теоремы следует, что точками экстремума могут быть не только стационарные точки, но и точки, в которых функция не имеет производной (точки разрыва производной). Определение. Стационарные точки функции Пример. Найти экстремумы функции 1) Находим область определение функции:
2) Находим производную функции и ее критические точки:
Таким образом,
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-10; просмотров: 59; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.84.155 (0.017 с.) |
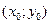 , равен значению производной функции в точке
, равен значению производной функции в точке 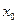 , т.е.
, т.е. 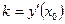
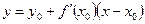
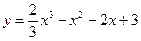 в точке с абсциссой
в точке с абсциссой 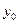 - значение данной функции при
- значение данной функции при 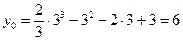
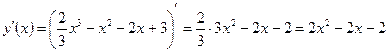
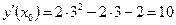 - угловой коэффициент касательной в точке
- угловой коэффициент касательной в точке 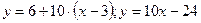
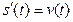
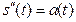
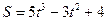 .
.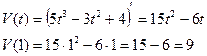
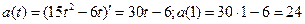
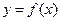 называется возрастающей на интервале
называется возрастающей на интервале 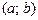 если для любых
если для любых 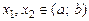 таких, что
таких, что 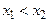 значения функции
значения функции 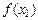 и
и 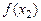 удовлетворяют неравенству
удовлетворяют неравенству 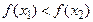 ((
((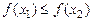 ).
).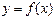 называется убывающей на интервале
называется убывающей на интервале 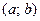 если для любых
если для любых 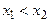 значения функции
значения функции 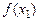 и
и 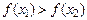 ((
((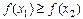 ).
).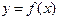 дифференцируема на интервале
дифференцируема на интервале 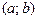 . Тогда
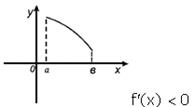
. Тогда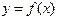 возрастает (убывает) на
возрастает (убывает) на 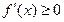 ,
, 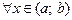 (
(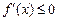 ,
, 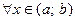 );
);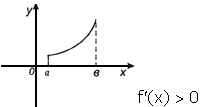
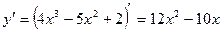 .
.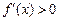 , и найдем промежутки возрастания функции.
, и найдем промежутки возрастания функции.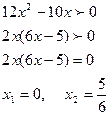

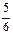
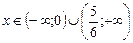
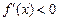 , получим
, получим 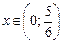 - промежуток убывания.
- промежуток убывания.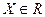 ,
, 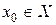 ,
, 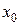 – внутренняя точка
– внутренняя точка 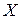 (т.е. существует некоторая окрестность точки
(т.е. существует некоторая окрестность точки 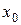 называется точкой максимума функции
называется точкой максимума функции 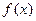 если существует такая
если существует такая 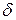 -окрестность точки
-окрестность точки 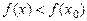 , для любых значений x принадлежащих
, для любых значений x принадлежащих 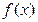 если существует такая
если существует такая 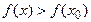 , для любых значений x принадлежащих
, для любых значений x принадлежащих 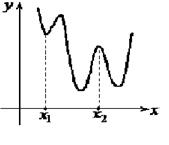 Теорема (необходимое условие экстремума, теорема Ферма). Если
Теорема (необходимое условие экстремума, теорема Ферма). Если 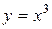 имеет стационарную точку
имеет стационарную точку 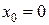 , которая не является ее точкой экстремума. Для функции, дифференцируемой в точке
, которая не является ее точкой экстремума. Для функции, дифференцируемой в точке 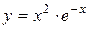 .
.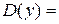 R.
R.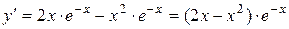 ;
;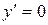 :
: 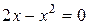 , ⇒
, ⇒ 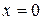 ,
, 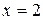 ;
;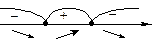 3) Определяем знак
3) Определяем знак 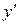 :
: 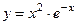 ,
,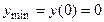 ,
, 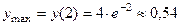 .
.


