
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение замечательных пределов.Стр 1 из 20Следующая ⇒
Первый замечательный предел Второй замечательный предел. Пример. 1) 2) 3) Пределы иррациональных выражений. Чтобы найти предел дроби, содержащей иррациональное выражение в случае, когда предел и числителя, и знаменателя равен нулю, надо перенести иррациональность из числителя в знаменатель, или из знаменателя в числитель и после этого сделать необходимые упрощения. Иррациональность переносится с помощью домножения и числителя и знаменателя дроби на выражение, сопряженное к иррациональности. После этого следует сделать преобразования и перейти к пределу, используя известные формулы: a 2- b 2 = (a - b)(a + b), a 3- b 3 = (a - b)(a 2 + ab + b 2). Пример. 1) Домножим числитель и знаменатель дроби на сопряженное иррациональное выражение с учетом, что (а - b)
2) Домножим числитель и знаменатель дроби на неполный квадрат суммы (а - b)
Непрерывность функции. Непрерывность функции в точке.
Определение. Функция y = f(x), определенная в окрестности некоторой точки х0, называется непрерывной в точке х0, если предел функции и ее значение в этой точке равны, т.е.
Пример. Исследовать функцию Найдем Так как Определение. Функция y = f(x), определенная в окрестности некоторой точки х0, называется непрерывной в точке х0, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, т.е.
Пример. Исследовать функцию Так как ∆х = х - х0 – приращение аргумента ∆y = y – y0 – приращение функции Тогда
Найдем Определение. Если функция f(x) определена в некоторой окрестности точки х0, но не является непрерывной в самой точке х0, то она называется разрывной функцией, а точка х0 – точкой разрыва. Пример непрерывной функции:
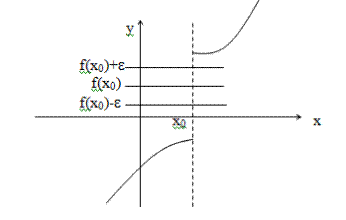
Пример разрывной функции:
Свойства непрерывных функций. 1) Сумма, разность и произведение непрерывных в точке х0 функций – есть функция, непрерывная в точке х0. 2) Частное двух непрерывных функций
3) Суперпозиция непрерывных функций – есть непрерывная функция. Это свойство может быть записано следующим образом: Если u = f(x), v = g(x) – непрерывные функции в точке х = х0, то функция v = g(f(x)) – тоже непрерывная функция в этой точке. Справедливость приведенных выше свойств можно легко доказать, используя теоремы о пределах.
|
|||||
|
Последнее изменение этой страницы: 2021-03-10; просмотров: 71; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.69.152 (0.006 с.) |

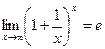
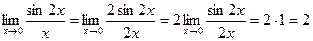
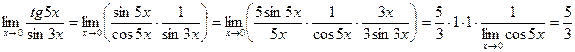
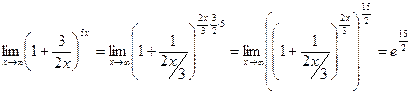
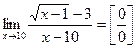 .
. (а + b) = a 2 - b 2 .
(а + b) = a 2 - b 2 .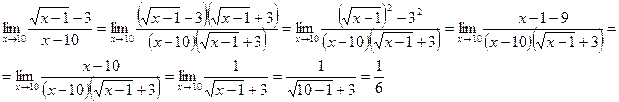 .
.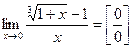
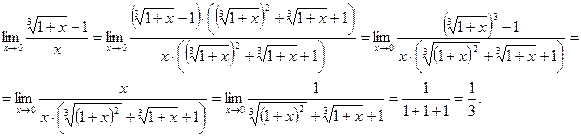
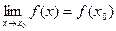
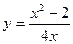 на непрерывность при x = 4.
на непрерывность при x = 4.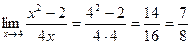 и
и 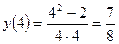
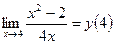 , следовательно, функция непрерывна в заданной точке.
, следовательно, функция непрерывна в заданной точке.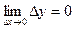
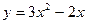 на непрерывность.
на непрерывность.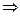 x0 = x - ∆х
x0 = x - ∆х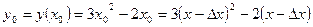
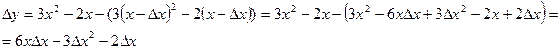
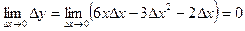 , следовательно функция непрерывна при любом значении x.
, следовательно функция непрерывна при любом значении x.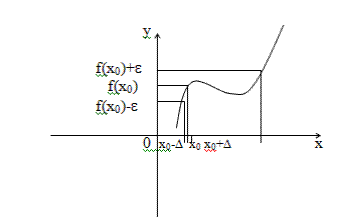
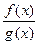 – есть непрерывная функция при условии, что g(x) не равна нулю в точке х0.
– есть непрерывная функция при условии, что g(x) не равна нулю в точке х0.


