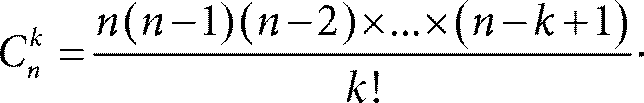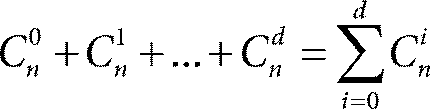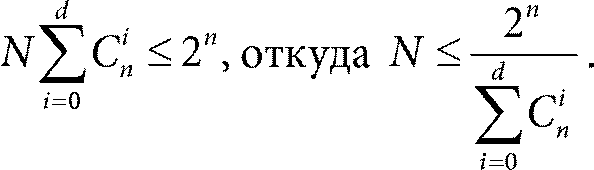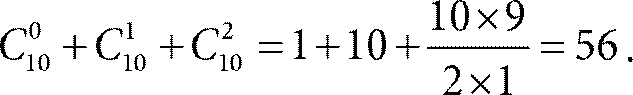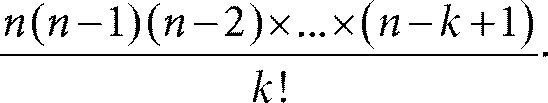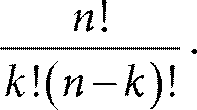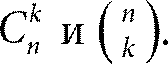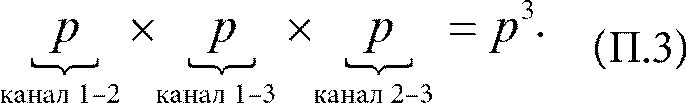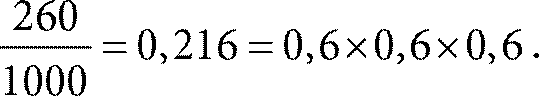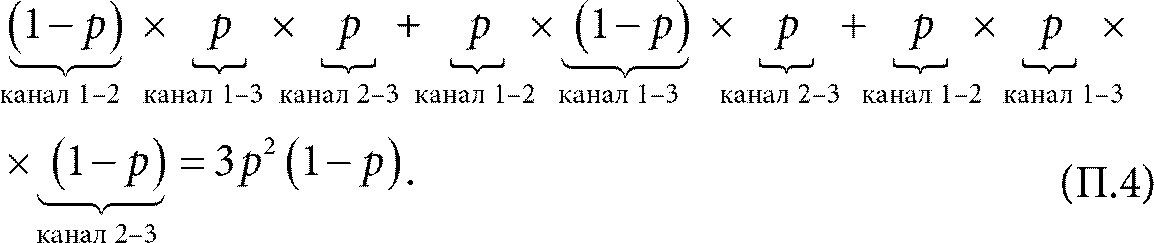Число последовательностей из нулей и единиц заданной длины

 

Для начала рассмотрим последовательности длины 5. Сколькими способами мы можем выбрать первый элемент последовательности? Очевидно, что вариантов 2: ноль или единица. Теперь давайте посмотрим на второй элемент. Для него у нас тоже есть два варианта, причем при любом выборе первого элемента последовательности. Значит, число способов выставить друг за другом первые два элемента равно четырем. Точно так же для каждого из этих четырех вариантов есть два способа выбрать третий элемент последовательности и так далее. В итоге для кодового слова длины 5 получаем

 

2 × 2 × 2 × 2 × 2 = 2⁵ = 32.

 

Аналогично число разных последовательностей длины 4 равно 2⁴ = 16, а число разных последовательностей длины 8 равно 2⁸ = 256. Для любой заданной длины n получаем 2 ⁿ разных последовательностей из нулей и единиц.

 

Граница Хэмминга

 

Допустим, мы пользуемся словами длиной n и наш код состоит из N таких слов.

Если код исправляет d ошибок, то шары Хэмминга с центрами в кодовых словах и радиусами d попарно не пересекаются. Объем шара (то есть количество слов в нем) нетрудно вычислить. Сколько слов отстают от центра шара на заданное расстояние k? Разумеется, столько, сколькими способами можно выбрать те k позиций из n возможных, в которых произойдут помехи. Это число способов называется числом сочетаний из п по k и обозначается C^k_n. Для того чтобы его записать, нам понадобятся произведения вида

 

k    × (k    − 1) × … × 2 × 1.

 

Такое произведение принято обозначать записью

 

k  !

 

и она читается как k факториал. Легко увидеть, что, конечно, 1! = 1, и принято считать, что 0! = 1. Заметим, что факториал уже встречался нам в главе 2 в разделе «Проклятие размерности». Там мы показали, что факториал растет очень быстро. Например, 25! – это колоссальное число.

Число сочетаний вычисляется по формуле

 

 

Мы приводим вывод этой известной формулы ниже, в приложении 3. Легко проверить, скажем, что C¹_n, и действительно мы можем выбрать одну позицию из n ровно n способами.

Значит, всего внутри шара

 

 

слов. Здесь слагаемое C ⁰ _n =1 – это число слов, отстоящих от центра на расстояние 0. Такое слово только одно – сам центр. Поскольку шары с центрами в кодовых словах попарно не пересекаются, то всего в них находится

 

 

различных слов. Но это количество заведомо не превосходит числа всех возможных кодовых слов, которое, как мы уже знаем, равно 2n. Таким образом,

 

 

Эта формула и есть граница Хэмминга. В нашем примере, когда n = 10, d = 2, получаем

 

 

Всего последовательностей длины 10 ровно 2¹⁰ = 1024. Получается, что максимальное количество кодовых слов не превышает 1024 ÷ 56 ≈ 18,2857. Поскольку число кодовых слов целое, оно не больше 18.

 

3. Число сочетаний из n по k

 

Мы рассмотрим число сочетаний на примере, связанном с кодированием. Давайте попробуем сосчитать, сколько существует слов длины n и веса k, k ≤ n. Напомним, что слово – это запись из нулей и единиц, а его вес – это количество единиц. Значит, нам нужно выбрать из n позиций k штук для расстановки на этих k выбранных позициях единиц. При этом ясно, что как только позиции будут выбраны, кодовое слово определяется однозначно. Выбрали, скажем, из шести позиций первую, четвертую и пятую – все, появилось кодовое слово 100110.

Хорошо, допустим, есть n позиций. Выбираем из них любую. Это можно сделать n способами. Для каждого из этих n способов выбора первой позиции из оставшихся n − 1 позиций снова выбираем любую. Для этого уже есть только n − 1 вариант. Итого количество способов зафиксировать первую и вторую позиции для единиц равно n (n − 1). Точно так же три позиции можно последовательно выбрать одним из n (n − 1) (n − 2) способов. И так далее. Для данного k будет всего

 

n    (n    − 1) (n    − 2) × … × (n    − k    + 1)

 

вариантов. Это и есть ответ? Не совсем!

Заметим, что в нашем примере, где n = 6 и k = 3, мы могли сначала выбрать, например, первую позицию, затем – четвертую и наконец – пятую, а могли сперва выбрать четвертую позицию, затем – пятую и лишь в конце – первую. И для каждого из подобных вариантов у нас получится одно и то же кодовое слово 100110. Сколько же раз в нашей формуле n (n − 1) (n − 2) × … × (n − k + 1) мы тем самым посчитали одно и то же кодовое слово? Смотрите, получая эту формулу, мы выбирали какие‑то последовательности номеров позиций: допустим, это были 1‑4‑5, 1‑5‑4, 5‑1‑4, 5‑4‑1, 4‑1‑5, 4‑5‑1. Видно, что все эти последовательности дают одно и то же слово из нулей и единиц. И видно, что их 6. Чтобы снова прийти к этому выводу не путем унылого перебора (которым мы сейчас занимались), а «весело и с умом», надо рассудить так: из трех чисел 1, 4, 5 мы можем сначала выбрать любое (3 варианта); затем вслед за ним расположить второе уже только одним из двух способов, а третье выбирается однозначно. Рассуждение дает нужный результат: число способов упорядочить числа 1, 4, 5 равно 3 × 2 × 1 = 6. Аналогично для любого k возникает формула k (k − 1) × … × 2 × 1 = k!. Напомним: по принятой в математике конвенции 0! = 1.

Что же мы имеем в итоге? Сначала мы вывели формулу n (n − 1) (n − 2) × … × (n − k + 1), потом сообразили, что в ней каждое множество позиций для единиц учтено k! раз. Это означает, что искомое количество кодовых слов равно

 

 

Заметим, что найденное выражение можно переписать в виде

 

 

Это так называемое число сочетаний из n по k, или биномиальный коэффициент. В настоящее время для него приняты два обозначения:

 

 

Назад к Главе 3

 

 

Приложения к главе 4

 

В качестве дополнительного материала к этой главе рекомендуем книгу Андрея «Модели случайных графов» {33}. Там в подробностях приводится доказательство теоремы Эрдеша – Реньи и много других интересных результатов из теории случайных графов.

 

1. Вероятность потери связи в мини‑сети

 

Рассмотрим мини‑сеть как в примере, приведенном в главе: три компьютера – 1, 2, 3 и три канала связи: 1–2, 1–3, 2–3. Допустим, что канал связи доступен с вероятностью р и недоступен с вероятностью 1 − p, где 0 < p < 1. Предположим, что каналы независимы друг от друга. Связь между всеми тремя компьютерами сохраняется в двух случаях.

Случай 1. Все три канала связи доступны. Соответствующая вероятность равна

 

 

Вероятности перемножаются потому, что каналы независимы друг от друга. Допустим, у нас тысяча мини‑сетей и p = 0,6. Тогда примерно в 600 из них будет доступен канал 1–2. Поскольку доступность канала 1–2 никак не влияет на канал 1–3, из нашей 1000 сетей оба канала 1–2 и 1–3 будут доступны в среднем 600 × 0,6 = 360 случаев. Чтобы вычислить среднее количество сетей, в которых доступны все три канала, надо взять долю 0,6 от 360, получаем 360 × 0,6 = 216. В результате вероятность доступности всех трех каналов равна

 

 

Случай 2. Два канала связи доступны и один недоступен. Недоступным может быть любой из трех каналов связи, поэтому случай 2 можно получить тремя разными способами. В результате соответствующая вероятность равна

 

 

Общая вероятность сохранения связи в сети теперь равна

 

(П.3) + (П.4) = p   ³ + 3 p   ² (1 − p   ) = 3 p   ² −2 p   ³.

 

Потеря связи хотя бы с одним из компьютеров тоже происходит в двух случаях, которые мы назовем случай 3 и случай 4.

Случай 3. Два канала связи недоступны и один доступен. Заметьте, что этот случай совершенно аналогичен случаю 2, только р и ( 1 − p) поменялись местами. Соответствующая вероятность равна

 

3 (p    − 1)² p  . (П.5)

 

Случай 4. Все три канала связи недоступны. Этот случай опять же аналогичен случаю 1, если поменять местами р и (1 − p). Соответствующая вероятность равна

 

(1 − p   )³. (П.6)

 

Вероятность, что хотя бы один компьютер окажется отрезанным от сети, равна

 

(П.5) + (П.6) = 3(1 − p   )² − 2(1 − p   )³. (П.7)

 

Естественно, если просуммировать все вероятности, то получится единица. Это очень красиво следует из бинома Ньютона третьей степени:

 

(П.3) + (П.4) + (П.5) + (П.6) = p   ³ + 3 p   ² (1 − p   ) + 3(p    − 1)² p    + (1 − p   )³ = (p    + (1 − p   ))³ = 1³ = 1

 

Если провести еще немножко алгебраических манипуляций, то можно переписать вероятность (П.7) по‑другому:

 

3(1 − p   )² − 2(1 − p   )³ = (1 − p   )² (3 − 2(1 − p   )) = (1 − p   )² (1 + 2 p   ) = (1 − p   ) ((1 − p   ) (1 + 2 p   )) = (1 − p   ) (1 + p    − 2 p   ²)

 

Легко проверить, что если p > ½, то вторая скобка меньше единицы. Получается, что если p > ½, то вероятность потери связи в мини‑сети меньше, чем вероятность потери связи в отдельно взятом канале, которая равна (1 − p).

Кроме того, выражение (П.7) всегда меньше, чем 3 (1 − p)². Поэтому если вероятность неисправности канала (1 − p) уменьшается, то вероятность потери связи в сети уменьшается еще быстрее. Когда вероятность (1 − p) очень мала, то термином −2 (1 − p)³ можно пренебречь. Тогда вероятность потери связи в сети приблизительно равна 3 (1 − p)². Если (1 − p) = 0,01 (то есть 1 %), то эта формула верна до третьего знака после запятой, что мы и видим в последней строчке табл. 4.1.