Правило 6: В некоторых случаях «и» означает умножение

Это правило практически противоположно предыдущему! Если мы хотим знать, чему равняется вероятность двух происходящих одновременно событий, для получения ответа мы можем умножить их вероятности – но только если эти два события НЕ взаимоисключающие! Возьмем две игральные кости. Если мы хотим узнать вероятность выпадения двух шестерок, нам нужно умножить вероятность двух событий: шанс получить 6 на одной кости равняется 1/6, а также шанс получить 6 на второй кости, который тоже равняется 1/6. Выходит, что шанс выпадения двух шестерок – 1/6 × 1/6 = 1/36. Вы могли бы одинаково успешно прийти к этому выводу путем перечисления, но это отняло бы у вас намного больше времени. В правиле 5 мы пытались узнать вероятность вытянуть туз ИЛИ бубну из колоды – правило не подействовало, потому что эти события не были взаимоисключающими. Теперь давайте попробуем узнать вероятность вытащить туза И любую карту бубновой масти. Иными словами, какая вероятность вытащить бубнового туза? Интуитивно мы понимаем, что этот шанс равен 1/52, но мы можем проверить это при помощи правила 6, поскольку знаем, что оба события не являются взаимоисключающими. Шанс вытащить туза равняется 4/52, а шанс вытащить бубну – 13/52. Умножим их: 4/52 × 13/52 = 52/2704 = 1/52. То есть правило работает и соответствует нашим умозаключениям.

Достаточно ли нам этих правил, чтобы решить проблему шевалье? Давайте взглянем на первую игру.

 

Первая игра: бросая одну кость четыре раза, шевалье выигрывал, если выпадала по крайней мере одна шестерка.

 

Мы уже пришли к тому, что могли пересчитать все результаты и получить ответ 671/1296, но это заняло бы целый час. Можно ли сделать это быстрее, используя те правила, которые мы уже знаем?

(Я хочу вас предупредить: дальше все будет несколько сложнее. Если вам это не сильно нужно, избавьте себя от лишней головной боли и просто пропустите правило 7. Если вам действительно интересна разгадка, приготовьтесь – оно того стоит.)

Если бы вопрос был о том, каковы шансы выпадения четырех шестерок при кидании одной кости четыре раза, это был бы вопрос с «И» для четырех не взаимоисключающих событий, что позволило бы нам обойтись правилом 6: 1/6 × 1/6 × 1/6 × 1/6 = 1/1296. Но в нашей задаче другое условие. Перед нами стоит вопрос с «ИЛИ» для четырех не взаимоисключающих событий (возможно, что шевалье получит больше, чем одну шестерку за четыре броска). Так что же нам делать? Первый способ – выделить взаимоисключающие события и суммировать их. Но есть и другой способ описать словами эту игру.

Какой шанс бросить кость и получить следующие результаты:

1. Четыре шестерки, ИЛИ

2. Три шестерки и одна не‑шестерка, ИЛИ

3. Две шестерки и две не‑шестерки, ИЛИ

4. Одна шестерка и три не‑шестерки?

Звучит сложновато, но мы имеем четыре взаимоисключающих события, и, если сможем узнать вероятность каждого из них, то сможем просто суммировать их и получить ответ на свой вопрос. Мы уже узнали вероятность события 1, используя правило 6: 1/1296. А что насчет 2? На самом ли деле 2 – это четыре разных взаимоисключающих события:

a) 6, 6, 6, не‑шесть;

b) 6, 6, не‑шесть, 6;

c) 6, не‑шесть, 6, 6;

d) не‑шесть, 6, 6, 6?

Вероятность выпадения шестерки равна 1/6, а вероятность выпадения не‑шестерки – 5/6. То есть вероятность каждого из этих событий – 1/6 × 1/6 × 1/6 × 5/6 = 5/1296. Теперь, если суммировать все четыре, получается 20/1296. Выходит, что вероятность 2 – 20/1296.

Что насчет 3? Здесь все так же, как и в предыдущем случае, но с большим количеством комбинаций. Сложно посчитать точное количество комбинаций с двумя шестерками и двумя не‑шестерками, но эта цифра равна шести:

a) 6, 6, не‑шесть, не‑шесть;

b) 6, не‑шесть, 6, не‑шесть;

c) 6, не‑шесть, не‑шесть, 6;

d) не‑шесть, 6, 6, не‑шесть;

e) не‑шесть, 6, не‑шесть, 6;

f) не‑шесть, не‑шесть, 6, 6.

И вероятность каждой из них – 1/6 × 1/6 × 5/6 × 5/6 = 25/1296. Суммируем все шесть и получаем 150/1296.

Осталось только 4, что является противоположностью 1:

a) не‑шесть, не‑шесть, не‑шесть, 6;

b) не‑шесть, не‑шесть, 6, не‑шесть;

c) не‑шесть, 6, не‑шесть, не‑шесть;

d) 6, не‑шесть, не‑шесть, не‑шесть.

Вероятность каждого из вариантов – 5/6 × 5/6 × 5/6 × 1/6 = 125/1296. Складываем все четыре и получаем 500/1296.

Выходит, мы высчитали вероятность для четырех взаимоисключающих событий:

1. Четыре шестерки – (1/1296);

2. Три шестерки и одна не‑шестерка – (20/1296);

3. Две шестерки и две не‑шестерки – (150/1296);

4. Одна шестерка и три не‑шестерки – (500/1296).

Суммируя эти четыре вероятности (в соответствии с правилом 5), мы получаем общую вероятность 671/1296, или около 51,77 %. Таким образом, мы можем видеть, насколько выгодной была эта игра для шевалье. Побеждая чаще, чем в 50 % случаев, он в конечном счете имел неплохие шансы на выигрыш, но вероятность была достаточно близка к середине, чтобы его друзья верили, что у них был шанс победить, – по крайней мере какое‑то время. Но этот результат определенно отличается от тех 66 %, на которые рассчитывал шевалье.

Тот же ответ мы могли бы получить путем перечисления, но это заняло бы слишком много времени. Некое перечисление все же имело место, но правила сложения и умножения позволяют нам перечислять все намного быстрее. Сможем ли мы таким путем получить ответ на вопрос о второй игре шевалье? Можем, но с 24 бросками двух костей мы потратили бы на это больше часа. Такой подход определенно быстрее перечисления, но, если проявить немного смекалки, можно еще ускорить процесс – и здесь на помощь приходит правило 7.

Правило 7: Один минус «да» = «нет»

Это больше интуитивное правило. Если шанс какого‑то события равен 10 %, то шанс, что это событие не произойдет, – 90 %. Почему это полезно? Потому что иногда вычислить вероятность возникновения какого‑то события сложнее, чем вероятность того, что оно НЕ произойдет.

Посмотрим на вторую игру шевалье. Вычислить вероятность выпадения по крайней мере одной двойной шестерки при 24 бросках было бы крайне трудно потому, что тогда бы нам пришлось сложить слишком много событий (1 двойная шестерка, 23 не‑шестерки, 2 двойные шестерки, 22 не‑шестерки и т. д.). Но что, если мы поставим вопрос иначе: какой шанс бросить две кости двадцать четыре раза и НЕ выбросить ни одной двойной шестерки? Теперь это вопрос с «И» для не взаимоисключающих событий, так что мы можем применить правило 6, чтобы узнать ответ. Но сначала мы еще два раза используем правило 7 – смотрите.

Шанс, что двойная шестерка выпадет после одного броска, равен 1/36. Итак, согласно правилу 7, вероятность того, что двойная шестерка не выпадет, – 1 – 1/36, или 35/36.

То есть, если применить правило 6 (умножение), шанс на то, что двойная шестерка не выпадет ни разу при 24 бросках, составит 35/36 × 35/36 двадцать четыре раза, или, чтобы было понятнее, 35/36 в 24‑й степени. Вы вряд ли захотите делать все эти подсчеты вручную, но если взять калькулятор, то вы увидите, что ответ – 0,5086, или 50,86 %. Но это вероятность проигрыша шевалье. Чтобы вычислить вероятность его выигрыша, нам нужно применить правило 7 еще раз: 1 – 0,5086 = 49,14 %. Теперь понятно, почему он проигрывал. Шанс на победу был настолько близким к половине, что его трудно было отличить от шанса на поражение, но после большого количества игровых сессий стало понятно, что поражение было более вероятным исходом.

Несмотря на то что все вопросы, связанные с вероятностью, можно решить посредством перечисления, правило 7 поможет вам сохранить много времени. На самом деле, это же правило мы могли бы применить и для первой игры шевалье.

Правило 8: Сумма нескольких линейных случайных исходов – это НЕ линейный случайный исход!

Не паникуйте. Как бы сложно это ни звучало, на самом деле все просто. «Линейный случайный исход» – это просто случайное событие, в котором все результаты имеют одинаковую вероятность. Бросание игральной кости – это отличный пример линейного случайного выбора. Хотя, если бросить несколько игральных костей, то возможные результаты НЕ будут иметь одинаковую вероятность. Если вы, например, бросаете две кости, то шанс получить семь довольно высок, в то время как шанс получить 12 намного меньше. Перечислив все возможности, вы поймете, почему так получается:

 

 

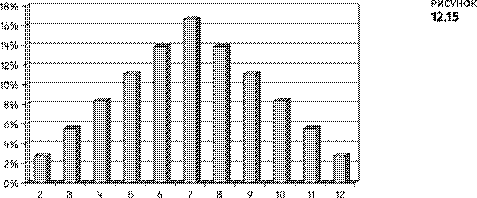
Посмотрите, как много в этой таблице 7 и всего одно 12! Мы можем продемонстрировать это на диаграмме под названием «Кривая распределения вероятности», чтобы увидеть шансы каждого из результатов.

 

 

Правило 8 кажется довольно очевидным, но я часто вижу, как начинающие дизайнеры составляют вместе два случайно выбранных числа, не понимая эффекта этого сложения. А иногда это именно тот эффект, который вам нужен, например, в игре Dungeons and Dragons игрок зарабатывает (виртуальные) очки навыков достоинством от 3 до 18, бросая три обычные (шестигранные) игральные кости. В результате в игре доминируют навыки достоинством 10 или 11, а 3 или 18 встречаются крайне редко, и это именно то, чего хотел дизайнер. А теперь представьте, насколько сильно игра отличалась бы от оригинальной версии, если бы, зарабатывая очки, игроки бросали один двадцатигранный кубик?

Геймдизайнеры, собирающиеся использовать механику шанса как инструмент для создания своих игр, должны понимать, какая кривая распределения вероятности нужна именно им, а также знать, как ее получить. С опытом к вам придет понимание того, насколько ценными инструментами могут быть кривые распределения вероятности.

Правило 9: Бросайте кости

Все вероятности, о которых мы говорили до этого, были теоретическими вероятностями, иными словами, тем, что должно случиться. Существует также практическая вероятность, которая является мерой того, что уже случилось. Например, если бросить кость, теоретическая вероятность выпадения шестерки составит ровно 1/6, или около 16,67 %. Но я мог бы вычислить практическую вероятность, бросив игральную кость 100 раз и записав, сколько раз мне попадались шестерки. Мне могут выпасть 20 шестерок из 100. В этом случае практическая вероятность составит 20 %, что не слишком сильно отличается от теоретической вероятности. Конечно, с увеличением количества попыток практическая вероятность все больше приближается к теоретической. Это правило получило название «метод Монте‑Карло» в честь знаменитого казино.

Положительной чертой использования метода Монте‑Карло для вероятности является то, что он не требует сложных математических подсчетов – вы проделываете одно и то же действие много раз и просто записываете результаты. Иногда результаты подобных тестов могут быть полезнее теоретической вероятности потому, что здесь мы имеем дело с реальными сущностями. Если существуют факторы, которые нельзя учесть при математических подсчетах (возможно, центр тяжести вашего кубика немного смещен к шестерке), или же эти подсчеты настолько сложные, что вы не можете составить теоретическую картину вашей ситуации, метод Монте‑Карло – это то, что вам нужно. Шевалье мог бы легко ответить на свой вопрос, бросая кости снова и снова, считая количество побед и разделяя их на число сделанных попыток.

Сегодня, в компьютерную эру, если вы хоть немного умеете программировать (или знаете того, кто умеет, – смотрите правило 10), вы можете без труда создать симуляцию миллиона попыток всего за несколько минут. На самом деле, это совсем не трудно – написать симуляцию игры и получить ответы на вопросы, касающиеся вероятности. Например, на какую клетку в «Монополии» фишки игроков встают чаще всего? Теоретически это невозможно выяснить – но, используя компьютер и метод Монте‑Карло, вы с легкостью выясните это, написав симуляцию бросания кубика и передвижения фишки по игровому полю несколько миллионов раз.