
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнения геодезической линии эллипсоида
Рассмотрим элементарный полярный треугольник APB' (рис.5.3), образованный дугами меридианов AP и B'P (Р – полюс земного эллипсоида, А и В′ – точки на эллипсоиде) и элементарной дугой геодезической линии
Рис. 5.3. К выводу дифференциального уравнения геодезической линии Пусть направление начального элемента геодезической линии
где: B, L – геодезические широта и долгота. Примечание. В этом разделе для геодезических широты и долготы используются обозначения B и L с целью подчеркнуть отличия этих координат от сферических, обозначаемых через φ и λ. Кроме того, для обозначения приведенной широты вместо символа j ¢¢ используется символ u. Уравнения (5.1) справедливы для участка любой кривой на поверхности, для которой справедливо также выражение для геодезической кривизны γ линии [8]:
где γ1 и γ2 – геодезическая кривизна координатных линий L = const (меридиана) и B = const (параллели). Геодезическая линия поверхности отличается тем, что ее геодезическая кривизна равна нулю: γ = 0. Приравнивая нулю правую часть выражения (5.2), получим дифференциальное уравнение геодезической линии:
Если считать, что DАРВ¢ практически является сферическим. Тогда по теореме косинусов для углов имеем
Применим формулу для косинуса суммы и разложим в ряд, получим
учитывая (5.1) приходим к уравнению
Уравнения (5.1) и (5.4) составляют систему дифференциальных уравнений геодезической линии земного эллипсоида:
Эта система уравнений служит основой для решения прямой и обратной геодезических задач. Геодезическая линия на поверхности эллипсоида вращения обладает важным свойством, описываемым теоремой Клеро: произведение радиуса параллели на синус азимута в каждой точке геодезической линии есть величина постоянная:
r · sinA = const. (5.6) Для доказательства рассмотрим плоскость меридиана, проходящего через точки A, С и Р (рис.5.3 и 5.4).
Рис. 5.4. К доказательству теоремы Клеро Если радиус параллели точки A обозначить через – dr = RN · dB · sinB. (5.7) Из уравнений (5.1) следует
Умножая первое из этих уравнений на rdA, а второе – на dr и складывая результаты, получим:
Преобразуя правую часть этого уравнения с учетом (5.7), получим:
или
В левой части получено выражение для полного дифференциала, которое можно проинтегрировать и найти: Из рис. 1.3 следует, что радиус параллели связан с величиной приведенной широты u и большой полуосью a эллипсоида соотношением:
поэтому уравнение (5.6) может быть переписано в виде
а теорема Клеро сформулирована следующим образом: для геодезической линии на эллипсоиде вращения произведение косинуса приведенной широты точки на синус азимута геодезической линии в той же точке есть величина постоянная. Записав (5.8) для точки пересечения геодезической линии с экватором, для которой u = 0, а азимут геодезической равен А o, найдем значение константы:
Уравнения (5.6), (5.8) и (5.9) используются при выводе формул для решения геодезических задач. Общие принципы решения геодезических задач на эллипсоиде Невозможность аналитического решения системы уравнений (5.5) в общем случае – с одной стороны, простота решения геодезических задач на сфере и малый эксцентриситет земного эллипсоида – с другой стороны, стали причиной того, что практически все разработанные методы решения геодезических задач на эллипсоиде включают следующие этапы [8]:
1. Вершины сфероидического треугольника APB (рис. 5.5), в котором Р – полюс эллипсоида, А и В – точки интереса при решении задач, отображаются на сферу. 2. Полученный на сфере треугольник А1Р1В1 (рис. 5.5) решается относительно неизвестных элементов методами сферической тригонометрии. 5. Осуществляется переход от вычисленных элементов сферического треугольника к соответствующим элементам исходного сфероидического треугольника.
Рис. 5.5 Отображение эллипсоида на сферу Система дифференциальных уравнений геодезической линии (ортодромии) на единичной сфере (ρ º 1), аналогичная системе (5.5), имеет вид:
где: j, l – сферические широта и долгота; a – азимут дуги большого круга; s – угловая длина дуги большого круга. Здесь единичная сфера выбрана для упрощения выкладок. При необходимости в систему (5.10) в виде множителя может быть введен отличный от единицы радиус сферы ρ. Методы решения геодезических задач различаются конкретным видом реализации указанных этапов. В первую очередь это относится к виду отображения уравнений (5.5) на (5.10), которое устанавливает связь между углами широты B, долготы L, азимута A и длиной дуги S на эллипсоиде, с одной стороны, и широтой j, долготой l, азимутом a, длиной дуги ρ·s на сфере, с другой стороны, с помощью функций ¦1 ¸ ¦4:
|
||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 485; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.242.141 (0.009 с.) |
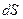 , соединяющей точки А и В′.
, соединяющей точки А и В′.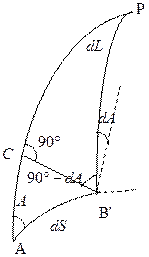
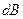 и
и 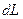 , схождение меридианов в точке B' – через
, схождение меридианов в точке B' – через 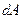 . Из элементарного треугольника AB'С имеем:
. Из элементарного треугольника AB'С имеем: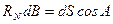 ,
,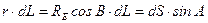 , (5.1)
, (5.1)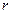 - радиус параллели;
- радиус параллели;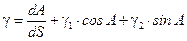 , (5.2)
, (5.2)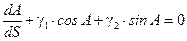 . (5.3)
. (5.3)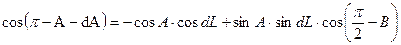 ,
,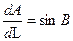 ,
,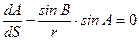 . (5.4)
. (5.4) (5.5)
(5.5)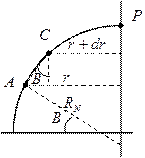
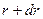 , длина элементарной хорды АС будет равна RN ∙ dB, а дифференциал радиуса параллели:
, длина элементарной хорды АС будет равна RN ∙ dB, а дифференциал радиуса параллели: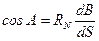 и
и 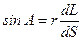 .
.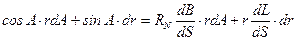 .
.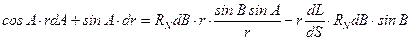 ,
,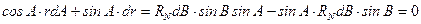 .
.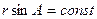 . Теорема доказана.
. Теорема доказана.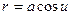 ,
, 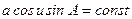 , (5.8)
, (5.8)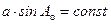 и перепишем теорему Клеро (5.8) в виде
и перепишем теорему Клеро (5.8) в виде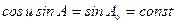 . (5.9)
. (5.9)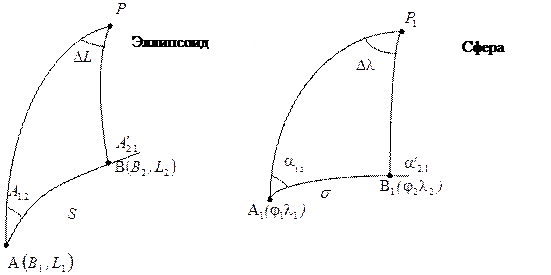
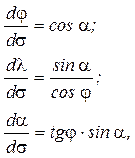 (5.10)
(5.10)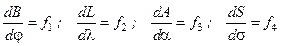 . (5.11)
. (5.11)


