
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы интегрирования определенного интеграла:
Непосредственное интегрирование. Пример:
2. Замена переменных. Пусть задан интеграл 1) j (a) = а, j (b) = b; 2) j (t) и j ¢ (t) непрерывны на отрезке [ a, b ]; 3) f (j (t)) определена на отрезке [ a, b ], то Тогда Пример:
3. Интегрирование по частям. Формула имеет вид: Пример:
Приближенное вычисление определенного интеграла Потребность в приближенном вычислении интеграла возникает тогда, когда не существует или неизвестен метод отыскания точного значения интеграла, и тогда, когда этот метод известен, но неудобен. Формула прямоугольников
Разобьем отрезок [ a, b ] на n равных частей, длины которых равны При таком разбиении имеем прямоугольники, площадь которых равна Тогда сумма площадей всех прямоугольников дает площадь ступенчатой фигуры, представляющую собой приближенное значение определенного интеграла и называемое общей формулой прямоугольников:
Формула трапеций
Подынтегральная функция в этом случае заменяется на вписанную ломаную. Геометрически площадь криволинейной трапеции заменяется суммой площадей вписанных трапеций. Замечание: чем больше взять точек n разбиения интервала, тем с большей точностью будет вычислен интеграл. Площади вписанных трапеций вычисляются по формулам:
После приведения подобных слагаемых получаем формулу трапеций:
Формула парабол (формула Симпсона или квадратурная формула)
Площадь криволинейной трапеции, ограниченной графиком функции f (x) заменим на площадь криволинейной трапеции, ограниченной параболой второй степени с осью симметрии, параллельной оси OY и проходящей через точки кривой, со значениями f (x 0), f (x 1), f (x 2).
Для каждой пары отрезков построим такую параболу.

      Уравнения этих парабол имеют вид Уравнения этих парабол имеют вид
Ax2 + Bx + C, где коэффициенты А, В, С могут быть легко найдены по трем точкам пересечения параболы с исходной кривой. Для определения А, В, С имеется система уравнений:
Выразается S через величины (1): C учетом этого: Отсюда выражение (2) примет вид: Тогда для каждой пары отрезков имеется:
Суммируя эти выражения, получаем формулу называемую формулой Симпсона: Пример: Вычислим приближенное значение определенного интеграла
Точное значение этого интеграла: 91.173. Для сравнения применим к этой же задаче формулу трапеций.
Несобственные интегралы 1.Несобственные интегралы первого рода Если функция
Если этот предел существует и конечен, то несобственный интеграл называется сходящимся; если предел не существует или бесконечен, то несобственный интеграл называется расходящимся. Теоремы о сходимости и расходимости: 1. Если на промежутке 2. Если при 3. Если сходится интеграл Примеры: 1. 2.
2.Несобственные интегралы второго рода (интеграл от разрывной функции) Если функция Если функция Замечание: внутренних точек разрыва II-го рода внутри отрезка может быть несколько. Теоремы о сходимости и расходимости: 1. Если на промежутке 2. Пусть функции 3. Если функция Задания для самопроверки №2 Вычислить: 1. 2. 3. 4. 5. 6. 7. 8. Исследовать на сходимость несобственные интегралы: a) b) c) d)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 113; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.45.92 (0.028 с.) |
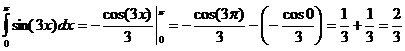 .
.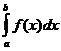 , где f (x) – непрерывная функция на отрезке [ a, b ]. Введем новую переменную в соответствии с формулой x = j (t).
, где f (x) – непрерывная функция на отрезке [ a, b ]. Введем новую переменную в соответствии с формулой x = j (t).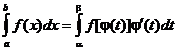 .
.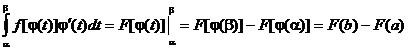
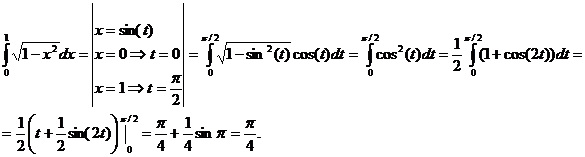
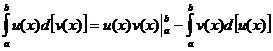 .
.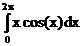 =
= 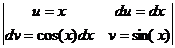 =
= 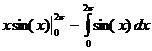 =
=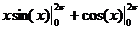 =
= 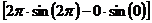 +
+ 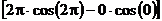 =0.
=0.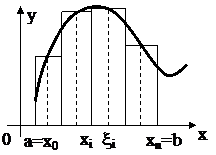 Пусть на отрезке [ a, b ] задана непрерывная функция f (x).
Пусть на отрезке [ a, b ] задана непрерывная функция f (x).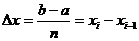 , где x1, x2, … xn – точки разбиения. Тогда можно записать, что
, где x1, x2, … xn – точки разбиения. Тогда можно записать, что 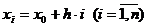 .
.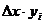 , где
, где 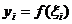 , а
, а 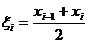 – некоторая точка на отрезке, которая в частности выбирается середина отрезка
– некоторая точка на отрезке, которая в частности выбирается середина отрезка 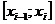 .
.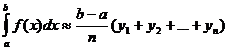 .
.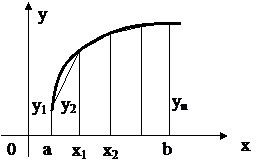 Эта формула является более точной по сравнению с формулой прямоугольников.
Эта формула является более точной по сравнению с формулой прямоугольников. ;
;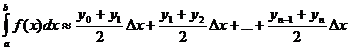 .
.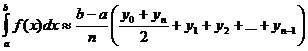
 Данный метод основан на разбиении дуги линии f (x), соответствующую [ a, b ], дугами парабол, что позволяет получить более точную формулу приближенного вычисления. Для этого разделим отрезок интегрирования [ a, b ] на четное число отрезков (2 m).
Данный метод основан на разбиении дуги линии f (x), соответствующую [ a, b ], дугами парабол, что позволяет получить более точную формулу приближенного вычисления. Для этого разделим отрезок интегрирования [ a, b ] на четное число отрезков (2 m).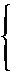
 (1)
(1)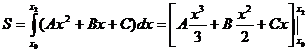 Если обозначим
Если обозначим  и примем х0 = - h, x 1 = 0, x 2 = h, то
и примем х0 = - h, x 1 = 0, x 2 = h, то 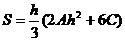 (2)
(2)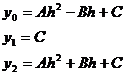
 .
.
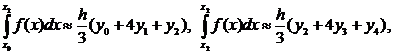 ...
...
 с помощью формулы Симпсона и формулы трапеций, разбив отрезок интегрирования на 10 частей. По формуле Симпсона получим:
с помощью формулы Симпсона и формулы трапеций, разбив отрезок интегрирования на 10 частей. По формуле Симпсона получим:
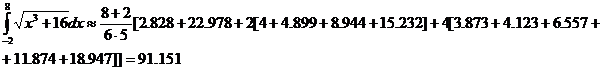
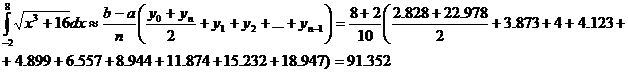
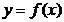 определена и непрерывна на любом отрезке [ a, b ], то несобственным интегралом с бесконечным пределом или несобственным интегралом первого рода называется интеграл:
определена и непрерывна на любом отрезке [ a, b ], то несобственным интегралом с бесконечным пределом или несобственным интегралом первого рода называется интеграл: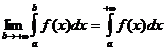 или
или  , или
, или , с – произвольное число.
, с – произвольное число.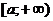 непрерывные функции
непрерывные функции 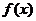 и
и 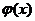 удовлетворяют условию:
удовлетворяют условию:  , то из сходимости интеграла
, то из сходимости интеграла  следует сходимости интеграла
следует сходимости интеграла 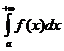 , а из расходимости интеграла
, а из расходимости интеграла 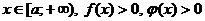 и существует конечные предел
и существует конечные предел 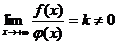 , то интегралы
, то интегралы 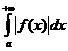 , то сходится и интеграл
, то сходится и интеграл  - не существует
- не существует 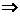 несобственный интеграл расходится.
несобственный интеграл расходится.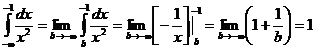 - интеграл сходится.
- интеграл сходится. и имеет разрыв II-го рода при
и имеет разрыв II-го рода при  , то несобственным интегралом неограниченной функции или несобственным интегралом второго родва называется интеграл:
, то несобственным интегралом неограниченной функции или несобственным интегралом второго родва называется интеграл:  или
или  , если функция терпит бесконечный разрыв в точке
, если функция терпит бесконечный разрыв в точке  .
.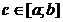 , то несобственным интегралом второго рода называют интеграл:
, то несобственным интегралом второго рода называют интеграл: 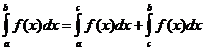 .
.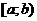 функции
функции 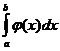 следует сходимости интеграла
следует сходимости интеграла 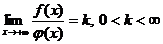 , то интегралы
, то интегралы 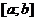 , имеет разрыв в точке
, имеет разрыв в точке  сходится, то сходится и интеграл
сходится, то сходится и интеграл 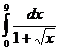 Ответ: 6-2ln4
Ответ: 6-2ln4 Ответ:
Ответ: 
 Ответ: 0
Ответ: 0 Ответ:
Ответ: 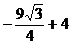
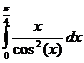 Ответ:
Ответ: 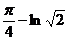
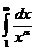 Ответ:
Ответ: 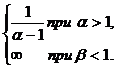
 Ответ: π
Ответ: π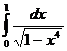 Ответ: сходится
Ответ: сходится Ответ: расходится
Ответ: расходится Ответ: сходится
Ответ: сходится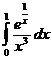 Ответ: расходится
Ответ: расходится


