
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегрирование иррациональных функций
Выделяют четыре основных типа интегралов, содержащих иррациональные функции: · Первый тип включает в себя интегралы, которые вычисляются методом замены переменной. Примеры: a)
b)
с)
Таким образом, к первому типу можно отнести следующие подынтегральные выражения, представленные в таблице 5.
Таблица 5.
· Ко второму типу относят интегралы вида
где Qn -1 (x) – многочлен степени равной п-1 с неопределёнными коэффициентами, λ – некоторый неопределённый коэффициент. Примеры: а) Здесь n = 3, поэтому соответствующее тождество имеет вид:
Продифференцируем полученное выражение:
Умножим на
Итого =
b) Здесь n = 4, поэтому соответствующее тождество имеет вид:
Дифференцируем полученное выражение:
Перегруппировываем:
· К третьему типу относят интегралы вида Интегрируются с помощью тригонометрической подстановки, которая называются подстановкой Эйлера. При необходимости выделяют под радикалом полный квадрат, т.е. Примеры: a) b)
с)
Таким образом, введя новые обозначения имеем следующие подынтегральные выражения, которые будут иметь соответствующие тригонометрические подстановки, представленные в таблице 6.
Таблица 6.
· Четвёртый тип Академиком Чебышевым П.Л.[1] было доказано, что интеграл от дифференциального бинома может быть выражен через элементарные функции только в следующих трех случаях: Таблица 7.
Примеры:
a)
b)
Примеры интегралов, не выражающихся через Элементарные функции 1. Интеграл вида a) Р(х) – многочлен третей или четвёртой степени без кратных корней, такой многочлен называется эллиптическим: · · · (0 < k < 1, h – комплексное число) b) Р(х) – многочлен степени выше четвертой, то интеграл называется ультраэллиптическим. c) Р(х) – многочлен выражаемый через элементарные функции называется псевдоэллиптическим. 2. 3. 4. 5. 6. Задания для самопроверки №1 Вычислить: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. Используя метод интегрирования по частям, доказать, что: а) b) c)
§2. Определенный интеграл Основные понятия и методы решения определенного интеграла
Пусть на отрезке [a, b] задана непрерывная функция f (x) [см. § 1]. Разобьём отрезок [a, b] произвольным образом на п частей точками Определённым интегралом от функции f (x) на отрезке [a, b] называется число равное пределу интегральных сумм при стремлении к нулю
Определённый интеграл обозначается символом Пусть на отрезке [ a, b ] задана непрерывная функция Геометрический смысл определённого интеграла: определённый интеграл равен площади «криволинейной трапеции» ограниченной функцией Теорема. Если функция f (x) непрерывна на отрезке [ a, b ], то определённый интеграл Отметим, что если оставить постоянным нижний предел интегрирования а, а верхний х изменить так, что бы Теорема ( Связь между неопределённым интегралом и определённым интегралами). Всякая непрерывная на отрезке [ a, b ] функция Теорема (Ньютона – Лейбница). Если функция F(x) – какая- либо первообразная от непрерывной функции f (x), то Основные свойства определенного интеграла: 1. 2. 3. 4. Если f (x) £ j (x) на отрезке [ a, b ] a < b, то 5. Если m и M – соответственно наименьшее и наибольшее значения функции f (x) на отрезке [ a, b ], то: 6. Теорема о среднем. Если функция f (x) непрерывна на отрезке [a, b], то на этом отрезке существует точка e такая, что 7. Для произвольных чисел a, b, c справедливо равенство: 8. 9.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 117; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.81.154 (0.051 с.) |
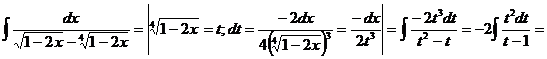


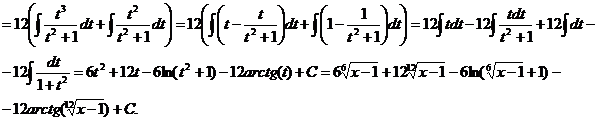

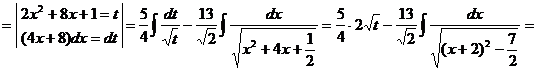

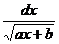




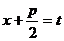
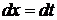
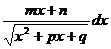
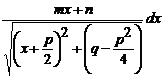
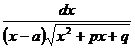
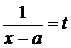 ,
,


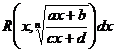 ,
где
,
где 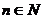
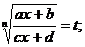


 , где Pn (x) – многочлен п- ой степени. Интеграл находится с помощью тождества, называемое методом неопределённых коэффициентов:
, где Pn (x) – многочлен п- ой степени. Интеграл находится с помощью тождества, называемое методом неопределённых коэффициентов: 
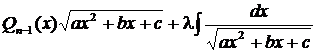 ,
,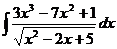
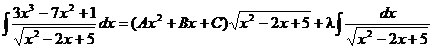 .
.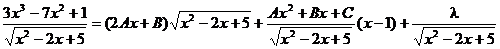
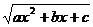 и сгруппируем коэффициенты при одинаковых степенях х:
и сгруппируем коэффициенты при одинаковых степенях х: =
= 
 =
= 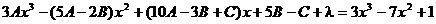

 =
=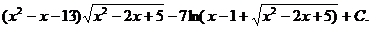
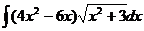
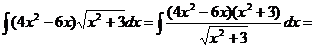


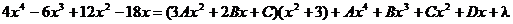
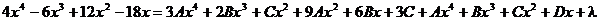
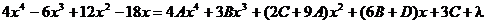

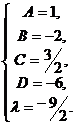

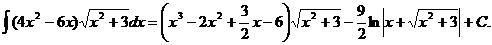
 .
.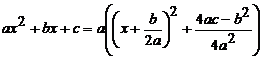 , и вводят обозначение:
, и вводят обозначение:  ,
, 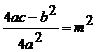 .
.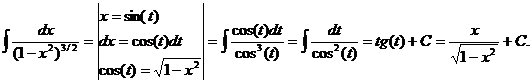
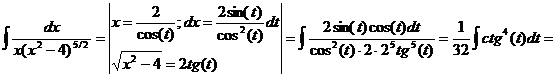


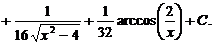
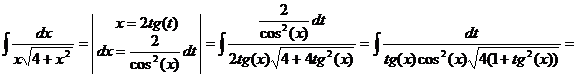
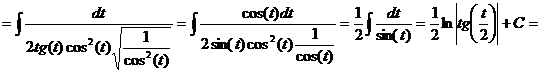
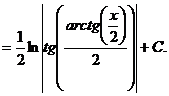
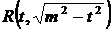
 или
или 


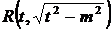
 или
или 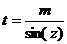
 или
или
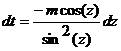
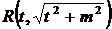
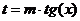 или
или 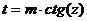
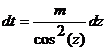 или
или

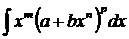 , где m, n, и p – рациональные числа, называют интегралами от дифференциального бинома.
, где m, n, и p – рациональные числа, называют интегралами от дифференциального бинома. или
или  ,
где l-общий знаменатель m и n.
,
где l-общий знаменатель m и n.
 – целое число
– целое число
 ,
где s – знаменатель числа р.
,
где s – знаменатель числа р.
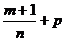 - целое число
- целое число
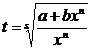 , где s – знаменатель числа р.
, где s – знаменатель числа р.



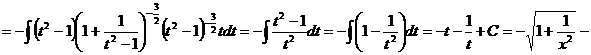
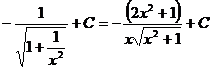
 :
: – эллиптический интеграл 1 рода;
– эллиптический интеграл 1 рода;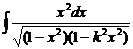 – эллиптический интеграл 2 рода;
– эллиптический интеграл 2 рода;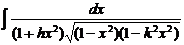 – эллиптический интеграл 3 рода.
– эллиптический интеграл 3 рода.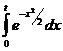 - интеграл Пуассона[2].
- интеграл Пуассона[2]. - интегралы Френеля[3].
- интегралы Френеля[3]. - интегральный логарифм.
- интегральный логарифм. - интегральная показательная функция.
- интегральная показательная функция.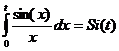 - интегральный синус.
- интегральный синус.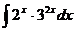 Ответ:
Ответ: 
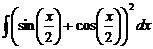 Ответ:
Ответ: 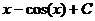
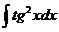 Ответ:
Ответ: 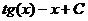
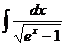 Ответ:
Ответ: 
 Ответ:
Ответ: 
 Ответ:
Ответ: 
 Ответ:
Ответ: 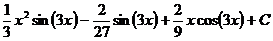
 Ответ:
Ответ: 
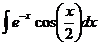 Ответ:
Ответ: 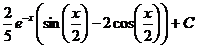
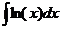 Ответ:
Ответ: 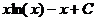
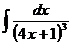 Ответ:
Ответ: 
 Ответ:
Ответ: 
 Ответ:
Ответ: 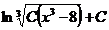
 Ответ:
Ответ: 
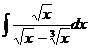 Ответ:
Ответ: 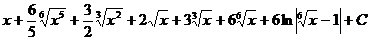
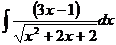 Ответ:
Ответ: 
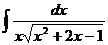 Ответ:
Ответ: 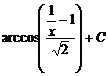
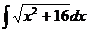 Ответ:
Ответ: 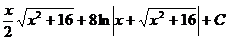
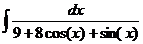 Ответ:
Ответ: 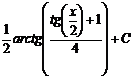
 Ответ:
Ответ: 
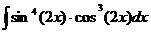 Ответ:
Ответ: 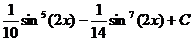
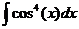 Ответ:
Ответ: 
 Ответ:
Ответ: 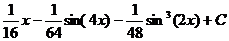
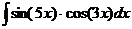 Ответ:
Ответ: 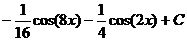
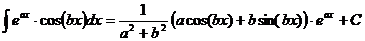 ;
; ;
; .
.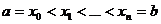 . На каждом отрезке
. На каждом отрезке  длины
длины 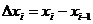 выберем произвольную точку
выберем произвольную точку 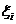 . Составим сумму
. Составим сумму 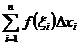 , называемую интегральной суммой для функции f (x) на отрезке [a, b].
, называемую интегральной суммой для функции f (x) на отрезке [a, b].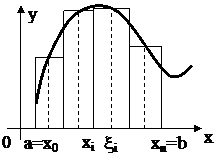 максимальной из длин отрезков разбиения:
максимальной из длин отрезков разбиения:  , этот предел конечен и не зависит от способов разбиения отрезка [a, b] на части и выбора точек
, этот предел конечен и не зависит от способов разбиения отрезка [a, b] на части и выбора точек 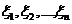 , на отрезках
, на отрезках  .
.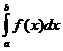 , где а называется нижним пределом, b называется верхним пределом, х называется переменной интегрирования, f (x) называется подынтегральной функцией, f (x) dx называется подынтегральным выражением, [ a, b ] – отрезок интегрирования.
, где а называется нижним пределом, b называется верхним пределом, х называется переменной интегрирования, f (x) называется подынтегральной функцией, f (x) dx называется подынтегральным выражением, [ a, b ] – отрезок интегрирования. . Фигура, ограниченная сверху графиком функции
. Фигура, ограниченная сверху графиком функции 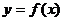 , снизу – осью Ox, сбоку прямыми x = a и x = b, называется криволинейной трапецией.
, снизу – осью Ox, сбоку прямыми x = a и x = b, называется криволинейной трапецией.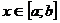 , то величина интеграла будет изменяться. Интеграл:
, то величина интеграла будет изменяться. Интеграл: 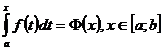 , называется определённым интегралом с переменным верхним пределом и является функцией верхнего предела х.
, называется определённым интегралом с переменным верхним пределом и является функцией верхнего предела х. имеет первообразную, равную интегралу
имеет первообразную, равную интегралу  , и тогда согласно определению неопределённого интеграла имеет место равенство
, и тогда согласно определению неопределённого интеграла имеет место равенство  .
.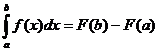 – это выражение известно под названием формулы Ньютона – Лейбница [4].
– это выражение известно под названием формулы Ньютона – Лейбница [4].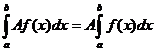 .
.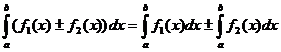 .
. .
.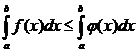 .
.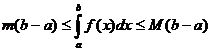 .
.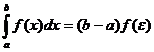 .
.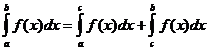 , где равенство выполняется, если существует каждый из входящих в него интегралов.
, где равенство выполняется, если существует каждый из входящих в него интегралов. .
.



