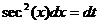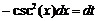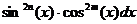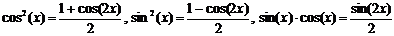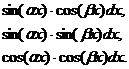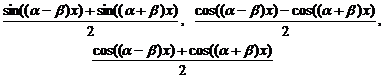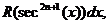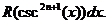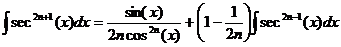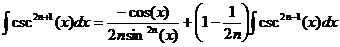Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегрирование рациональных дробей
Дробно-рациональной функцией называется функция вида: Замечание: Если m < n, то рациональную дробь называется правильной. Если m ³ n, то рациональную дробь называется неправильной. Примеры: a) b)
c)
d)
Интеграл · рекуррентной формулы: Она выведена в курсе математического анализа: Следовательно,
· интегрирования по частям:
В таблице 3 приведены общие виды правильных рациональных дробей и способы их интегрирования с помощью замены переменной. Таблица 3.
m, n – натуральные числа (m ³ 2, n ³ 2) и D <0.
Подынтегральные выражения не вошедшие в таблицу 3 интегрируются с помощью метода неопределенных коэффициентов. Теорема (метод неопределенных коэффициентов). Если P (x) = (x - a) a …(x - b) b (x 2 + px + q) l …(x 2 + rx + s) m ) (причем множители типа x 2 + px + q неразложимы на действительные множители первой степени), то эта дробь может быть разложена на сумму простейших дробей:
Примеры: a) Подынтегральное выражение представляется в виде суммы простейших дробей После освобождения от знаменателей, получается:
Сгруппировываются члены с одинаковыми степенями:
В итоге получается:
b) Так как дробь неправильная, то выделяется целая часть:
6x5 – 8x4 – 34x3 + 12x2 2x2 + 3 9x3 + 8x2 – 76x - 7 9x3 – 12x2 – 51x +18 20x2 – 25x – 25 Следовательно,
Получаются: Следовательно, корни этого уравнения: 3; -2; 1/3. Отсюда Получившееся подынтегральное выражение раскладывается на элементарные дроби:
Применяем метод произвольных значений, суть которого состоит в том, что в полученное выражение подставляем поочередно (по числу неопределенных коэффициентов) значения х. Для упрощения вычислений принимают точки, при которых знаменатель дроби равен нулю. В нашем случае: 3, -2, 1/3. Получаем:
В итоге получаем:
1.4. Интегрирование тригонометрических функций · Метод тождественных преобразований. Примеры: a)
b)
· Метод замены переменной. Примеры: c)
d)
e)
· Метод универсальной тригонометрической подстановки (универсальной замены). Примеры: f)
g)
h)
Интеграл вычисляется методом неопределенных коэффициентов:
Получается:
Учитывая выше сказанное, представим основные типы тригонометрических функций в виде таблицы 4. Таблица 4.
Здесь R – обозначение некоторой рациональной функции от переменных sin (x) и cos (x). Функции sec(x)=1/cos(x) и csc(x)=cosec(x)=1/sin(x).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 110; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.203.68 (0.025 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
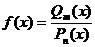 , где
, где 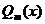 - многочлен степени m,
- многочлен степени m, 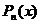 - многочлен степени n.
- многочлен степени n.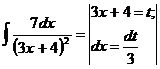 =
= 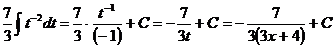 ;
;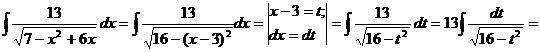
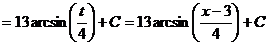 .
.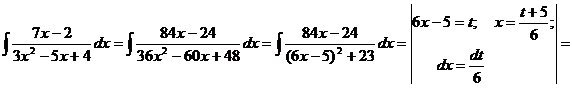
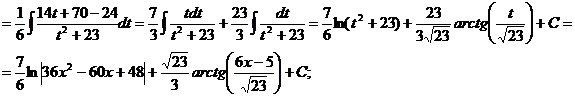
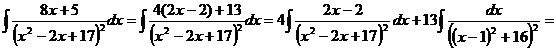
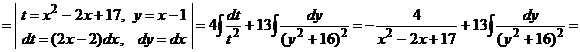
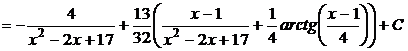 .
.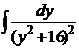 вычисляется с помощью:
вычисляется с помощью: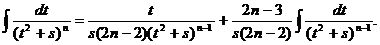
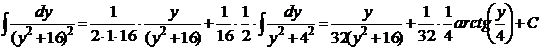 .
.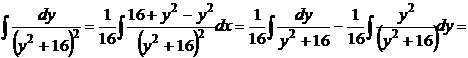
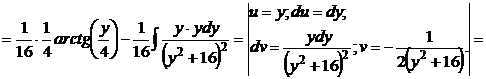
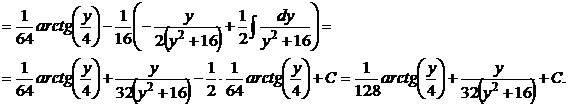
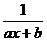
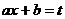
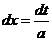
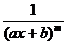
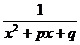
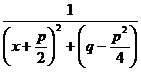
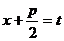
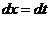
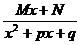
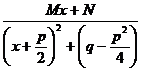
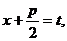
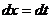 и раскладывается на сумму двух интегралов
и раскладывается на сумму двух интегралов
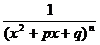
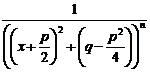
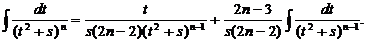
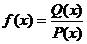 - правильная рациональная дробь, где знаменатель имеет вид:
- правильная рациональная дробь, где знаменатель имеет вид: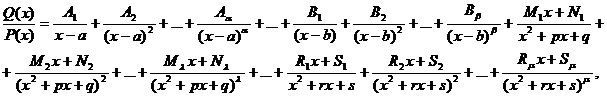 где Ai, Bi, Mi, Ni, Ri, Si – некоторые постоянные величины.
где Ai, Bi, Mi, Ni, Ri, Si – некоторые постоянные величины.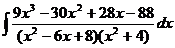 =
= 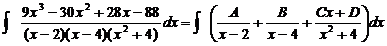
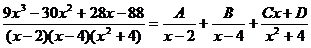 .
.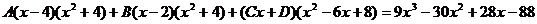 .
.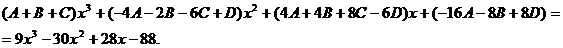
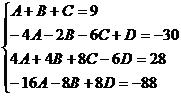
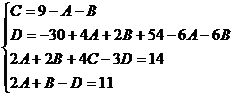
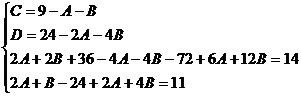
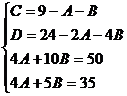
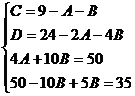
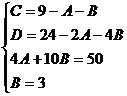
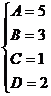
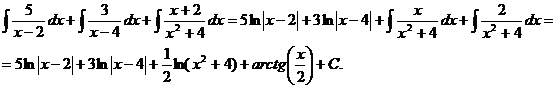
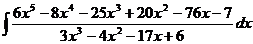 .
. 6x5 – 8x4 – 25x3 + 20x2 – 76x – 7 3x3 – 4x2 – 17x + 6
6x5 – 8x4 – 25x3 + 20x2 – 76x – 7 3x3 – 4x2 – 17x + 6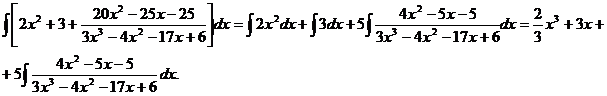 Для нахождения корней уравнения
Для нахождения корней уравнения 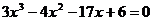 применяем схему Горнера:
применяем схему Горнера: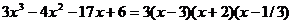 .
.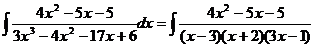 .
.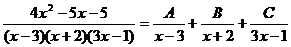
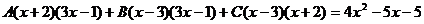
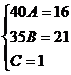
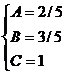
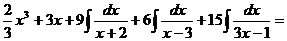
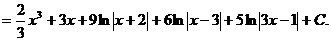
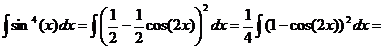
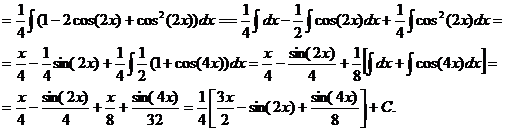
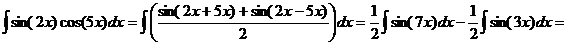
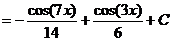
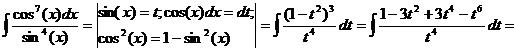
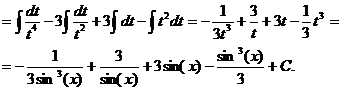
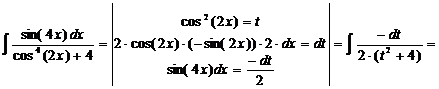
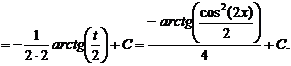
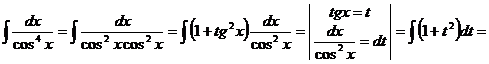
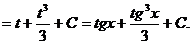
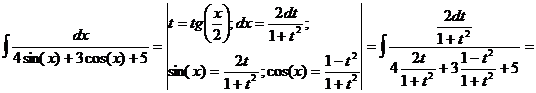
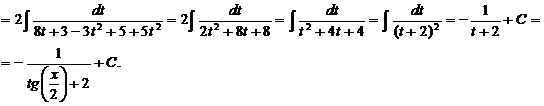
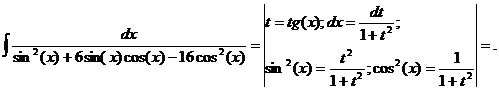
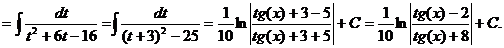

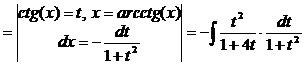
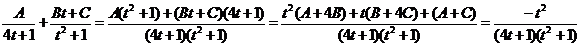
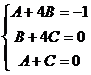
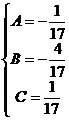
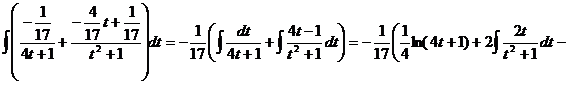
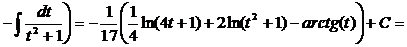
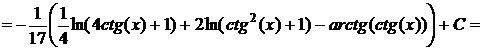
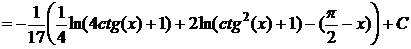 .
.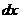
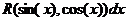
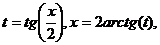
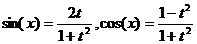
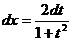
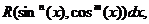
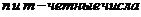
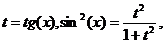
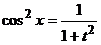
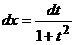
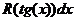
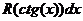
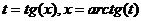
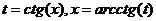
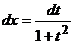
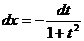
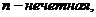
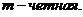
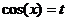
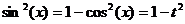
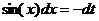
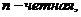
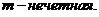
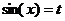
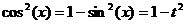
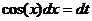
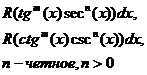
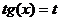 ,
, 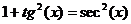
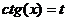 ,
,