
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема 1 (критерий подгруппы).
Непустое подмножество
Доказательство. 1. Необходимость - очевидно, по определению, если 2. Достаточность. Если Тогда для всякого Примечание. Этот критерий - фактически эквивалентное свойство, которое могло бы быть принято в качестве определения подгруппы. Теорема 2. Если
Доказательство. Если Но каждая
Пример. Подгруппы Пример. Группа подстановок 1) Ассоциативность есть.
С другой стороны, 2) Нейтральный элемент 3) Обратный элемент. Если Пример. Подгруппа Пример. Подмножество всех нечётных подстановок - не образует подгруппу, потому что: произведение подстановки и обратной к ней (обе нечётные) это тождественная подстановка, а она содержит 0 инверсий, значит - чётная, но тогда она не принадлежит этому подмножеству.
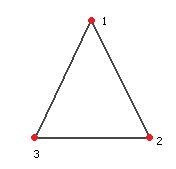
Пример. Группы движений и симметрий правильных n-угольников. Например, для треугольника. Каждый поворот или зеркальное отражение, при котором 3 вершины переходят в какие-то другие, соответствует подстановке.
Но при этом можно заметить, что всякое отражение может быть получено как композиция какого-то одного базового отражения (например, где меняются вершины 1 и 2) и поворота.
Для
ЛЕКЦИЯ 2. 14.11.2020 Кольца Теперь рассмотрим множества не с одной, а с двумя различными операциями. Интуитивно вам уже известны такие примеры: сложение и умножение на множестве чисел, к тому же, для них известен закон дистирибутивности:
Определение. Пусть 1) 2) 3) операции сложения и умножения связаны законами дистрибутивности: Тогда Если существует нейтральный элемент по умножению, то кольцо называется кольцом с единицей. Если операция умножения коммутативна, то называется «коммутативное кольцо». Примеры. 1)Числовые кольца. 2) Кольцо функций. Функции, заданные на
По сложению есть противоположный элемент.
3) Множество векторов в 3-мерном пространстве относительно операции векторного умножения. Это пример некоммутативного кольца, и без единицы. Лемма. 1. При умножении любого элемента на 2. Произведение 1-го элемента на противоположный ко 2-му это то же самое, что произведение противоположного 1-му на 2-й, и равно противоположному к их суммарному произведению, т.е. Доказательство. 1. 2.
Определение. Непустое подмножество Примеры. Все непрерывные на Теорема 1. (критерий подкольца). Непустое множество 1) Доказательство. Необходимость - очевидно. Если подкольцо, то произведение принадлежит, кроме того, Достаточность. Если для любой пары элементов
Операция ассоциативна и на подмножестве, поэтому Дистрибутивность также сохраняется на подмножестве. Вывод:
Обратимые элементы. Определение. Пример. В кольце В кольцах В кольце функций (с поточечным умножением) обратимые элементы это те функции, которые ни в одной точке не обращаются в 0.
Делители нуля Определение. Если Пример в кольце функций. В числовых множествах делителей нуля нет. В кольце матриц есть, например,
Теорема 2. Обратимый элемент кольца не может являться делителем нуля. Доказательство. Пусть
но с другой стороны, Значит,
Замечание. Обратное утверждение к теореме 2 неверно, т.е. из того, что он не делитель нуля, не следует, что обратимый. Пример: в кольце
Теорема 3. О мультипликативной группе кольца. Все обратимые элементы кольца Доказательство. Докажем, что если
Кроме того, Обратный к любому элементу также Идеал кольца. Определение. Подкольцо Пример во множестве функций. Все функции, обращающиеся в 0 в точке
Кольца вычетов. Определение. Два целых числа называются сравнимыми по модулю n, если при делении на n они дают одинаковые остатки, т.е. если их разность делится на n: Обозначается Например, числа 1, 4, 7, 10, 13,... дают при делении на 3 остаток 1. При этом разность любых из них делится на 3. Таким образом, множество
Свойства сравнимости. 1. 2. 3. Из этих 3 свойств следует, что сравнимость является отношением эквивалентности в Свойство 4. Докажем это свойство, оно не очевидно.
Пример. 4 и 7 5 и 8 разность 3 тогда 9 и 15 разность кратна 3 тоже. Свойство 5. Докажем это свойство.
Пример. 4 и 7 5 и 8 разность 3 тогда 20 и 56 разность 36, кратна 3.
Если Классы вычетов попарно не пересекаются: Обозначим Это можно сделать, так как из свойств 4 и 5, ранее доказанных, следует, что произведение не зависит от выбора представителя класса.
Итак, на конечном множестве из n элементов заданы 2 операции, сложение и умножение. Множество классов вычетов тоже образует кольцо Другое обозначение класса вычетов: Например,
- - - Перерыв - - - Очевидно, Составим таблицы сложения. Первый пример - для
Обратите внимание, 3 простое число, и при умножении в каждой строке есть все классы. Составим таблицы сложения и умножения для кольца
Так, к примеру, 2+3=5, но число 5 превосходит 4 на 1, то есть попадает в класс
Далее для доказательства свойств колец вычетов нам понадобятся некоторые факты из теории чисел (доказывали их на практике). Лемма. Если Следствие. Если Теорема 4. Пусть (1) (2) числа Доказательство. (1) (2)
Теорема 5. Пусть
Доказательство. (1)
(2)
Следствие. Пусть Эквивалентны 3 факта: 1) 2) 3)
Следствие. Если n простое число, то подкольцами в (Идея док-ва. Так как, если n простое число, то оно взаимно-просто относительно любого из чисел В кольце
ЛЕКЦИЯ 3. 16.11.2020 Поля Определение. Пусть Отличие от кольца: Примеры.
Каждое такое число обратимо, и обратное имеет тот же вид.
Аналогично существуют Кольцо классов вычетов
Определение. Подмножество Примеры. Теорема 1. (Критерий подполя). Пусть 1) 2) Доказательство.
Определение. Поле Теорема 2. 1) Пусть
Кроме того, любой элемент обратим, т.е. Теперь, для любого 2) Если
| Поделиться:
| |
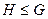 группы
группы 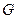 является подгруппой
является подгруппой 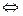
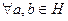 выполняется:
выполняется: 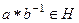 .
. 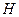 сама является группой, то
сама является группой, то 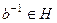 ,
, 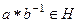 .
. 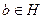 , то
, то 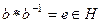 .
. 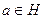 , обратный также принадлежит, ведь
, обратный также принадлежит, ведь 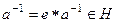 . □
. □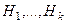 - подгруппы группы
- подгруппы группы 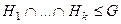 тоже подгруппа.
тоже подгруппа.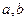
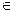
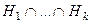 , то
, то 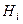 .
. 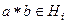 (всем), а значит, их пересечению. Кроме того,
(всем), а значит, их пересечению. Кроме того, 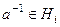 для всех номеров
для всех номеров 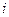 , а значит, тоже
, а значит, тоже 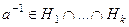 . В итоге,
. В итоге, 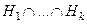 подгруппа. □
подгруппа. □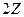 и
и 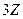 , а их пересечение
, а их пересечение 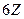 - все числа, кратные 6.
- все числа, кратные 6.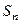 называется симметрической группой степени n. Число элементов
называется симметрической группой степени n. Число элементов 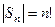
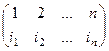 ,
, 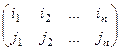 ,
, 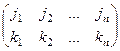 .
.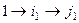 а затем
а затем 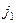 переходит в
переходит в 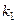 , в итоге
, в итоге 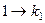 .
.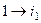 а
а 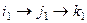 в результате композиции 2-й и 3-й подстановок, в итоге опять
в результате композиции 2-й и 3-й подстановок, в итоге опять 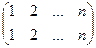 .
.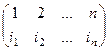 то обратный
то обратный 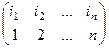 , где в верхней строке все n разных чисел и их можно расставить по порядку.
, где в верхней строке все n разных чисел и их можно расставить по порядку. 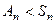 - группа всех чётных подстановок. Кол-во элементов
- группа всех чётных подстановок. Кол-во элементов 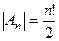 .
.
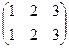
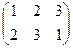
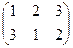 вращения
вращения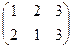
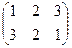
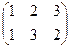 зеркальные отражения
зеркальные отражения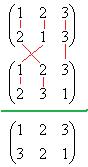
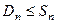 называется группой Диэдра. Для
называется группой Диэдра. Для 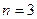 (в случае треугольника) она совпадает с группой всех подстановок,
(в случае треугольника) она совпадает с группой всех подстановок,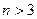 , уже
, уже 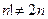 .
. 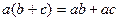 ,
, 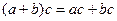 .
.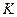 - множество, на котором заданы две бинарные операции (как правило, сложение и умножение), удовлетворяющие условиям:
- множество, на котором заданы две бинарные операции (как правило, сложение и умножение), удовлетворяющие условиям: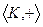 абелева группа
абелева группа 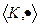 полугруппа (т.е. только ассоциативность)
полугруппа (т.е. только ассоциативность)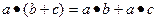 ,
, 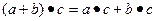 .
.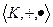 называется кольцом.
называется кольцом.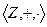 ,
, 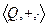 ,
, 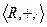 коммутативные кольца с единицей.
коммутативные кольца с единицей.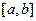 , можно поточечно складывать и умножать.
, можно поточечно складывать и умножать.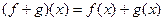 ,
, 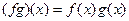 .
.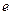 по сложению - тождественно нулевая функция
по сложению - тождественно нулевая функция 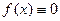 .
. 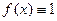 .
.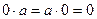 .
. 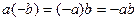 .
.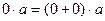 =
= 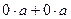 , вычтем
, вычтем 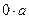 из обеих частей равенства, получим
из обеих частей равенства, получим 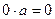 .
. 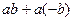 =
= 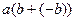 =
= 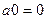
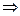
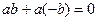
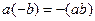 .
.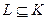 называется подкольцом, если оно само образует кольцо относительно операций, заданных в кольце
называется подкольцом, если оно само образует кольцо относительно операций, заданных в кольце 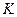 .
.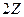 подкольцо в
подкольцо в 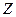 ,
, 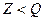 ,
, 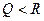 .
.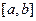 функции - подкольцо в кольце всех (по поточечному умножению, см. пример был выше).
функции - подкольцо в кольце всех (по поточечному умножению, см. пример был выше).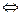
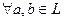 :
: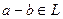 2)
2) 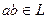 .
. 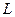 является подгруппой по сложению, тогда для любого
является подгруппой по сложению, тогда для любого 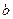 элемент
элемент 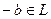 , а значит и
, а значит и 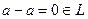 , а тогда и
, а тогда и 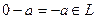 , то есть для каждого элемента противоположный тоже
, то есть для каждого элемента противоположный тоже 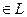 , т.е.
, т.е. 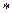 ).
).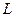 полугруппа.
полугруппа.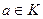 называется обратимым, если
называется обратимым, если 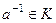 .
. 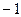 .
.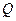 или
или 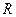 обратимые элементы все, кроме 0.
обратимые элементы все, кроме 0.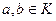 ,
, 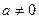 ,
, 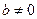 , но при этом
, но при этом 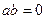 , то
, то 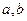 называются делителями нуля.
называются делителями нуля.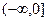
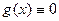 на
на 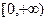 . Тогда
. Тогда 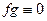 на всей числовой оси.
на всей числовой оси.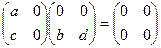 .
.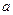 обратим, и пусть всё же он является делителем 0, тогда есть какой-то
обратим, и пусть всё же он является делителем 0, тогда есть какой-то 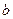 , что
, что 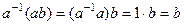 ,
,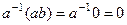 , тогда
, тогда 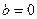 .
.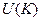 ).
). 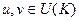 то
то 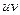 тоже обратим, т.е.
тоже обратим, т.е. 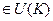 . Докажем, что обратный имеет такой вид:
. Докажем, что обратный имеет такой вид: 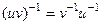 .
.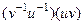 =
= 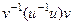 =
= 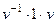 =
= 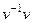 = 1.
= 1.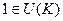 , ведь сам элемент 1 обратим, и обратный к нему тоже 1.
, ведь сам элемент 1 обратим, и обратный к нему тоже 1.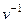 , то он автоматически обратим, обратный к нему это исходный
, то он автоматически обратим, обратный к нему это исходный 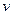 . □
. □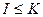 называется идеалом, если
называется идеалом, если 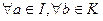
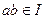 .
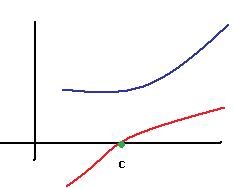
. 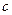 , образуют идеал. Если умножить произвольную функцию на такую, то произведение приобретает свойство
, образуют идеал. Если умножить произвольную функцию на такую, то произведение приобретает свойство 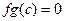 .
. 
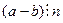 .
. 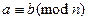 .
. 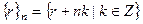 - класс вычетов по модулю n.
- класс вычетов по модулю n. 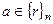 означает, что
означает, что 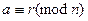 .
. 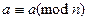 . Рефлексивность
. Рефлексивность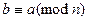 . Симметричность
. Симметричность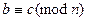
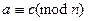 . Транзитивность
. Транзитивность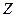 , и
, и 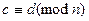
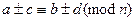
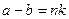 ,
, 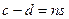 тогда
тогда 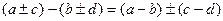 =
=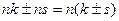 , то есть снова делится на n.
, то есть снова делится на n. 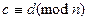
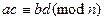
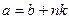 ,
, 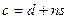
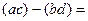
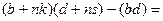
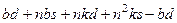 =
=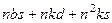 , это делится на n.
, это делится на n.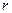 называется представителем класса
называется представителем класса 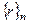 .
. 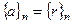 .
.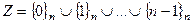
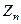 - множество всех классов вычетов по модулю n. Введём на этом конечном множестве из n элементов операции сложения и умножения:
- множество всех классов вычетов по модулю n. Введём на этом конечном множестве из n элементов операции сложения и умножения: 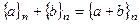 ,
, 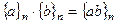 .
.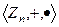 . Это коммутативное кольцо с единицей.
. Это коммутативное кольцо с единицей.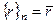 .
. 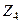 =
= 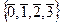 .
. 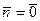 в
в 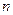 само делится на
само делится на 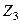
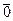
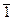
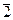
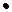
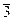
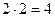 , но 4 эквивалентно 0, поэтому
, но 4 эквивалентно 0, поэтому 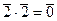 . Как видим, в этой системе могут быть и делители нуля, а в строке, соответствующей
. Как видим, в этой системе могут быть и делители нуля, а в строке, соответствующей 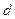 НОД чисел
НОД чисел 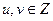 , что
, что 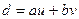 .
. 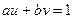 .
.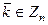 . Эквивалентны следующие условия:
. Эквивалентны следующие условия: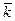 является обратимым элементом в
является обратимым элементом в 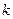 ,
, 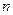 взаимно просты.
взаимно просты. 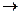 (2). Пусть
(2). Пусть 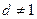 . Тогда
. Тогда 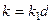 . Обратимость означает, что
. Обратимость означает, что 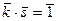 . То есть, остаток от деления
. То есть, остаток от деления 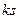 на
на 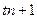 . Докажем, что это невозможно. Пусть
. Докажем, что это невозможно. Пусть 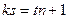 , тогда
, тогда 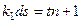 . Левая часть равенства делится на
. Левая часть равенства делится на 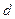 , тогда и правая должна делиться на
, тогда и правая должна делиться на 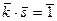 невозможно, и
невозможно, и 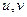 , такие что
, такие что 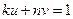 . Тогда
. Тогда 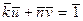 , но ведь
, но ведь 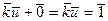 , так что
, так что 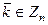 .
. 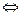
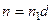 , очевидно
, очевидно 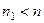 . Рассмотрим
. Рассмотрим 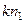 =
= 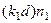 =
= 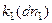 =
= 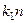 . То есть,
. То есть, 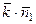 =
= 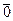 , то есть
, то есть 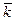 делитель нуля. Итак, если он не делитель нуля, то
делитель нуля. Итак, если он не делитель нуля, то 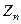 (нетривиальных подколец нет).
(нетривиальных подколец нет).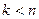 , и в каждой строке в таблице умножения - некая перестановка из всех элементов).
, и в каждой строке в таблице умножения - некая перестановка из всех элементов). 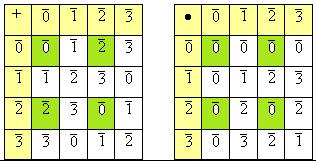
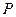 - коммутативное кольцо с единицей, в котором каждый ненулевой элемент обратим. В таком случае
- коммутативное кольцо с единицей, в котором каждый ненулевой элемент обратим. В таком случае 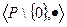 - абелева группа, она называется мультипликативной группой поля.
- абелева группа, она называется мультипликативной группой поля.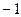 ).
).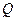 поле рациональных чисел.
поле рациональных чисел.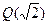 =
= 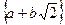 , где
, где 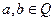 расширение поля
расширение поля 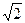 . Произведение пары таких чисел тоже имеет данный вид.
. Произведение пары таких чисел тоже имеет данный вид.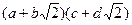 =
= 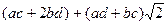 .
. 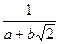 =
= 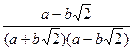 (домножили на «сопряжённое», чтобы использовать формулу разности квадратов). Далее,
(домножили на «сопряжённое», чтобы использовать формулу разности квадратов). Далее,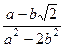 =
= 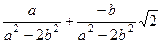 .
. 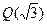 ,
, 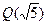 и т.д. Но все эти расширения поля
и т.д. Но все эти расширения поля 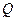 - лишь часть поля
- лишь часть поля 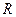 .
. 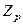 является полем
является полем 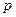 простое число (тогда нет делителей нуля, каждый элемент обратим).
простое число (тогда нет делителей нуля, каждый элемент обратим).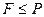 называется подполем, если оно само является полем относительно введённых в
называется подполем, если оно само является полем относительно введённых в 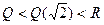 ,
, 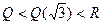 , но при этом сами
, но при этом сами 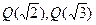 не являются одно подполем другого.
не являются одно подполем другого.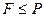 .
. 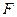 является подполем
является подполем  выполнены условия:
выполнены условия: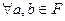 :
: 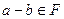 ,
,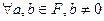 :
: 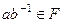
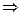 Если
Если 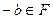 , и тогда
, и тогда 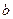 обратим, тогда
обратим, тогда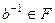 , а тогда
, а тогда 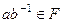 .
.
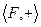 группа по сложению, а
группа по сложению, а 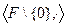 группа по умножению. Тогда
группа по умножению. Тогда 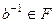 , а значит
, а значит 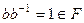 .
.  .
. и
и 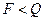 . Тогда
. Тогда 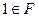 .
. 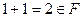 ,
, 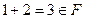 ,...
,... 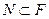 .
.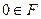 и для всякого
и для всякого 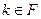 противоположное
противоположное 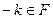
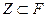 .
.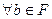 :
: 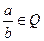 ,
, 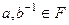
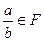 . Итак,
. Итак, 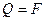 .
.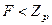 .
. 


