
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Симплекс-метод. Определение оптимальной производственной программы предприятия
Графический метод, рассмотренный выше, обычно используется для решения двумерных задач линейного программирования, но его невозможно применить для решения задач более высокой размерности. В этих случаях используют специальные методы. Одним из них является симплекс-метод. Симплекс-метод представляет процесс последовательного (от итерации к итерации) улучшений плана (решения) задачи по специальному алгоритму. В результате симплексных преобразований получают симплексную таблицу, в которой: 1) если в строке целевой функции 2) если в строке целевой функции 3) если в строке целевой функции Это правило применяется при решении задач на максимум. При решении задач симплекс-методом исходным моментом является определение начального допустимого базисного решения (начального опорного плана). Все задачи, решаемые симплекс-методом, по способу нахождения начального опорного плана можно отнести к трем группам: 1) задачи линейного программирования с явно выраженным начальным опорным планом; 2) задачи линейного программирования, для нахождения начального опорного плана которых необходимо использовать простые алгебраические преобразования; 3) задачи линейного программирования, для нахождения начального опорного плана которым необходимо использовать метод искусственного базиса. Рассмотрим решение задачи из каждой группы. Пример 4.1. Предприятие выпускает продукции трех видов, расходуя при этом четыре вида ресурсов. Норма затрат ресурсов и прибыль от реализации каждого вида продукции, а также объем каждого вида ресурса представлены в табл. 4.1. Таблица 4.1
Требуется найти такую программу производства, при которой достигается максимум прибыли от реализации продукции.
Решение Пусть
Общая прибыль составит
Переменные
Прежде чем решить задачу симплекс-методом, необходимо математическую постановку данной задачи привести к общей постановке задачи линейного программирования (канонической форме), т.е. от ограничений-неравенств перейти к ограничениям-равенствам. Для этого в каждое из неравенств вводится по одной дополнительной переменной:
С экономической точкизрения дополнительные переменные Для построения первой симплекс-таблицы необходимо определить начальное допустимое базисное решение. Данная задача относятся к задачам линейного программирования с явно выраженным начальным опорным планом. В качестве начальной выбирается ситуацию, когда предприятие ничего не выпускает, т.е. Для заполнения первой симплекс-таблицы необходимо представить математическую постановку задачи линейного программирования (ограничения-равенства и целевую функцию
Первая симплекс-таблица имеет вид, представленный в табл. 4.2. Таблица 4.2
Процесс отыскания оптимального решения заключается в переходе от одной симплекс-таблицы к другой, пока не будет достигнуто оптимальное решение (план) задачи.
Для получения новой симплекс-таблицы необходимо воспользоваться следующим алгоритмом: 1. Выбирается генеральный столбец, т.е. столбец с наибольшим по модулю отрицательным коэффициентом в строке 2. В генеральном столбце определяется генеральный коэффициент по минимуму отношения
где
3. На место генерального коэффициента записывается величина, обратная генеральному коэффициенту
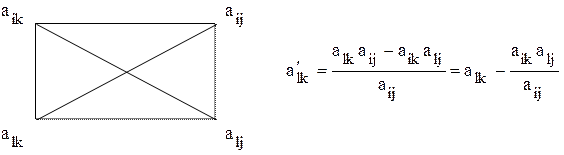
4. Все значения коэффициентов генеральной строки, т.е. строки, где находится генеральный коэффициент, делятся на значение генерального коэффициента и записываются в эту же строку. 5. Все значения коэффициентов генерального столбца делятся на значение генерального коэффициента и записываются в тот же столбец с противоположным знаком. 6. Все остальные коэффициенты находятся по правилу прямоугольника
Используя вышеприведенный алгоритм, устанавливается, что генеральным будет столбец, соответствующий свободной переменной Таблица 4.3
Анализируя полученные значения коэффициентов при свободных переменных в строке целевой функции F, устанавливаем, что данное решение еще не является оптимальным, так как есть отрицательные значения коэффициентов Таблица 4.4
Далее строится четвертая симплекс-таблица (табл. 4.5). Таблица 4.5
Все значения коэффициентов при свободных переменных в строке целевой функции
Таким образом, при выпуске предприятием продукции вида А в объеме 1 ед., вида В − 1 ед., вида С − 3 ед. максимальная прибыль составит 54 тыс.руб. При этом материалы, оборудование I и II групп используется полностью, а рабочая сила на 5 человек недоиспользуется. Пример 4.2. Предприятие располагает тремя группами технологического оборудования, на котором может изготавливаться семь видов изделий. Трудоемкость обработки и прибыль от реализации каждого вида изделия, а также фонд времени работы оборудования представлены в табл. 4.6. Таблица 4.6
Требуется организовать такую программу производства, при которой достигается максимум прибыли от реализации продукции, причем изделий вида А необходимо изготовить не менее 30 шт., вида В − не более 30 шт., вида С − ровно 10 шт., видов Е и F – в комплектности 1:3 и вида G − не менее 10 шт. и не более 50 шт. Решение Решение задачи начинается с математической постановки задачи. Все условия (ограничения) данной задачи можно разделить на две группы: 1) ограничения по ресурсу
где 2) ограничения по ассортименту
Целевая функция для данной задачи имеет вид
Одно из ограничений по ассортименту является жестким. Это позволяет исключить из дальнейшего рассмотрения изделия вида C (т.е. условие выполняется, изделий вида Cвыпущено ровно 10 шт.), что повлечет за собой корректировку фонда времени работы оборудования. Математическая постановка задачи примет следующий вид: - ограничения по ресурсу
- ограничение по ассортименту
- целевая функция
Данная задача не имеет явно выраженного начального допустимого базисного решения. Действительно, если осуществить переход от ограниченийнеравенств к ограничениям-равенствам путем введения дополнительных переменных
Для нахождения начального допустимого базисного решения таких задач можно использовать простые алгебраические преобразования. Метод простых алгебраических преобразований для нахождения начального опорного плана используется в задачах, содержащих неравенства вида «≥», которые связывают только одну переменную Идея метода простых алгебраических преобразований заключается в переходе от старых переменных к новым следующим образом
Математическая постановка в новых переменных имеет следующий вид: - ограничения по ресурсу
- ограничения по ассортименту
- целевая функция
Путем введения дополнительных переменных
Начальное допустимое базисное решение будет иметь вид
Базисные переменные необходимо выразить через свободные и представить ограничения-равенства и целевую функцию в виде удобном для формирования первой симплекс-таблицы
Для получения оптимального решения задачи построим симплекс-таблицы (табл. 4.7 - 4.10). Таблица 4.7
Таблица 4.8
Таблица 4.9
Таблица 4.10
В последней симплекс-таблице (табл. 4.10) содержится оптимальное решение
Затем осуществляется переход к старым переменным
Таким образом, при выпуске изделия вида A в объеме 30 шт., вида В − 30 шт., вида С − 10 шт., изделия вида D не выпускаются, вида Е − 164 шт., вида F − 492 шт., вида G − 50 шт. будет получена максимальная прибыль в размере 2410 тыс.руб. Для планирования объемов производства характерны также задачи на минимум. Они имеют некоторые особенности. Например, при структуре ограничений, изображенной на рис. 4.1, не имеет смысла решать задачу на минимум, поскольку целевая функция всегда будет проходить через начало координат и равняться нулю. Если же среди ограничений будут неравенства вида «≥», получаем иную структуру области допустимых решений и оба типа оптимизации экономически содержательны.
Рис. 4.1. Графическое представление оптимальных планов задач на минимум и максимум:
Смысл ограничения вида “≥” поясним в нижеследующих задачах. Пример 4.3. Месячная производственная программа состоит из трех видов изделий. Изделия проходят обработку на двух операциях. Трудоемкость обработки, себестоимость и оптовая цена каждого вида изделия, а также фонды времени работы оборудования приведены в табл. 4.11. Таблица 4.11
Требуется определить такую программу производства, при которой достигается минимум затрат на производство при условии выполнения директивного уровня плана, который составляет 1800 тыс.руб. Решение Осуществляем математическую постановку задачи. Пусть
Тогда ограничения по ресурсу
и целевая функция
Данная задача так же, как и задача из примера 4.2, не имеет явно выраженного допустимого базисного решения, так как имеется ограничения вида «≥». Однако это ограничение-неравенство связывает более чем одну переменную
Если принять переменные
Также как переменная
Тогда математическая постановка задачи будет следующей
Переменные
Для того чтобы воспользоваться алгоритмом на максимум, умножим обе целевые функции на -1
Затем базисные переменные следует выразить через свободные переменные и представить ограничения-неравенства и целевые функции в виде, удобном для заполнения симплекс-таблицы
В первых двух симплекс-таблицах (табл. 4.12, 4.13) предпоследняя строка отводится для целевой функции -F, а последняя строка – -f. Решение ведётся по последней строке -f. Завершается применение метода искусственного базиса лишь в том случае, если значение целевой функции -f и коэффициентов при свободных переменных в этой функции станут равными нулю, за исключением коэффициента при переменной Таблица 4.12
Таблица 4.13
Из табл. 4.13 следует, что
Поэтому завершается применение метода искусственного базиса, который позволил привести к нулю переменную
Зная начальное допустимое базисное решение, можно найти оптимальное решение данной задачи (табл. 4.14, 4.15). Таблица 4.14
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
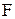 имеется хотя бы один отрицательный коэффициент и в столбце, соответствующем этому коэффициенту, имеется хотя бы один положительный коэффициент, то решение может быть улучшено;
имеется хотя бы один отрицательный коэффициент и в столбце, соответствующем этому коэффициенту, имеется хотя бы один положительный коэффициент, то решение может быть улучшено;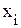 − количество выпускаемой продукции i-гo вида, тогда система неравенства, отражающих ограничения на имеющийся объем ресурсов по каждому виду, будет следующей
− количество выпускаемой продукции i-гo вида, тогда система неравенства, отражающих ограничения на имеющийся объем ресурсов по каждому виду, будет следующей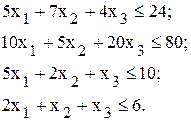
 .
.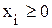
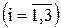 .
.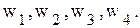 В результате получаем
В результате получаем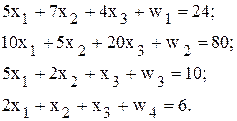
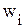 характеризуют объем неиспользуемого в плане ресурса i-го вида.
характеризуют объем неиспользуемого в плане ресурса i-го вида.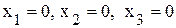 . Эти значения переменных можно принять за начальное допустимое базисное решение. При этом все имеющиеся ресурсы не расходуются, т.e.
. Эти значения переменных можно принять за начальное допустимое базисное решение. При этом все имеющиеся ресурсы не расходуются, т.e. 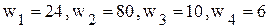 . Переменные
. Переменные 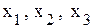 называются свободными, a
называются свободными, a 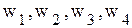 − базисными. При решении задачи линейного программирования симплекс-методом свободные переменные всегда равны нули, а базисные переменные − больше нуля (в некоторых случаях базисная переменная может принимать нулевое значение, тогда такой базис называется вырожденным).
− базисными. При решении задачи линейного программирования симплекс-методом свободные переменные всегда равны нули, а базисные переменные − больше нуля (в некоторых случаях базисная переменная может принимать нулевое значение, тогда такой базис называется вырожденным).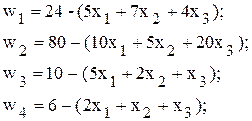
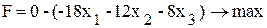 .
.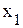 ↑
↑
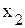
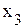
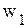
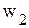

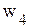
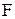 .
. ,
,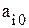 - i-й коэффициент в столбце "Свободный член";
- i-й коэффициент в столбце "Свободный член";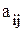 - i-й коэффициент в генеральном столбце.
- i-й коэффициент в генеральном столбце.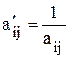 .
.
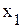 , а генеральный коэффициент находится в строке, соответствующей базисной переменной
, а генеральный коэффициент находится в строке, соответствующей базисной переменной 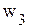 , т.е.
, т.е. 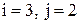 . Поменяв местами переменные
. Поменяв местами переменные 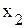 ↑
↑
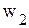
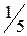
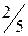
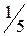
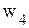
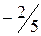
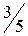
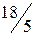
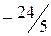
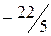
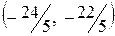 , следовательно, необходимо продолжить решение задачи. Повторив указанные выше действия, выстраивается третья симплекс-таблица (табл. 4.4)
, следовательно, необходимо продолжить решение задачи. Повторив указанные выше действия, выстраивается третья симплекс-таблица (табл. 4.4)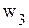
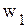
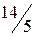
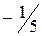
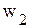
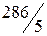
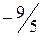
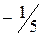
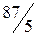
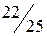
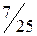
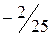
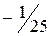
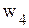
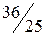
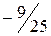
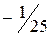
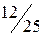
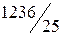
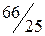

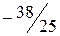
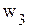
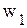
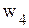



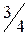
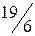
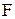 неотрицательны, следовательно, получено оптимальное базисное решение (план)
неотрицательны, следовательно, получено оптимальное базисное решение (план)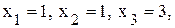
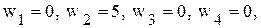
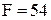 .
.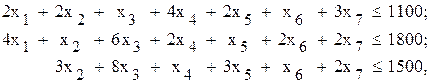
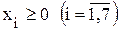 .
.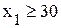 (ограничение снизу);
(ограничение снизу);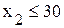 (ограничение сверху);
(ограничение сверху);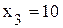 (жесткое ограничение);
(жесткое ограничение);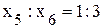 (условие комплектности);
(условие комплектности);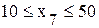 (двустороннее ограничение).
(двустороннее ограничение).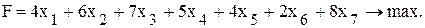
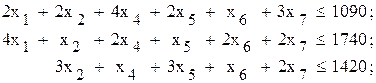
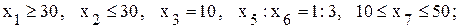
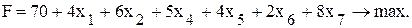
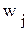 и принять неизвестные
и принять неизвестные 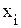 вкачестве свободных переменных, т.е. равными нулю, то некоторые базисные переменные
вкачестве свободных переменных, т.е. равными нулю, то некоторые базисные переменные 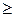 ». В рассматриваемой задаче таких неравенств два
». В рассматриваемой задаче таких неравенств два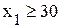 и
и 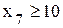 .
. ,
, 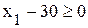 ,
, 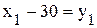 Þ
Þ 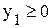 ,
, 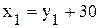 ;
;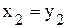 Þ
Þ 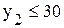 ;
;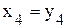 ;
;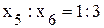 ,
, 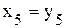 Þ
Þ 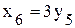 ;
; ,
, 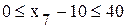 ,
, 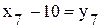 Þ
Þ 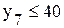 ,
, 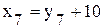 .
.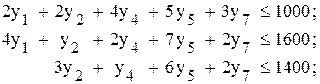
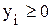
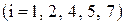 ;
;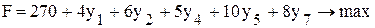 .
.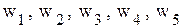 осуществляется переход от ограничений-неравенств к ограничениям-равенствам
осуществляется переход от ограничений-неравенств к ограничениям-равенствам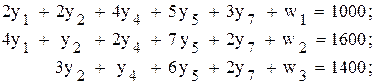
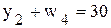 ;
;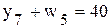 .
.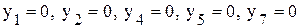 (свободные переменные);
(свободные переменные);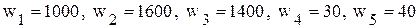 (базисные переменные).
(базисные переменные).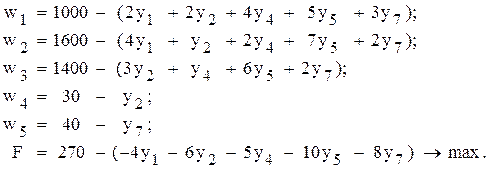
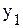
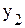
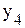
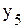 ↑
↑
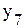
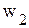
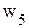
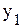
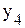
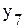
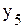
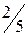
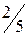
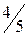
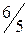
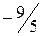
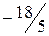
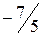
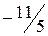
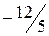
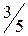
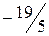
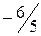

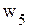
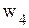
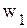
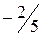
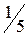
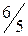
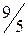
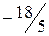
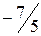
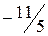
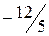

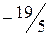
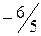
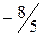
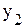
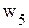
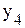
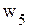
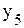
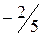
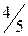
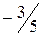
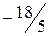
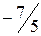
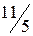
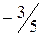
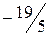
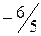
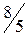

 .
.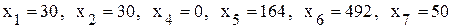 .
.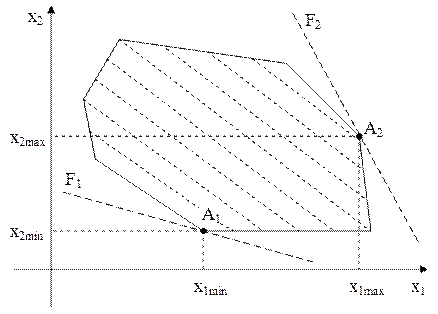
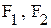 - целевые функции для решения задач на минимум и максимум;
- целевые функции для решения задач на минимум и максимум;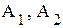 - точки оптимума для задач обоих типов;
- точки оптимума для задач обоих типов;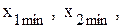
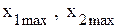 - оптимальные планы задач обоих типов
- оптимальные планы задач обоих типов
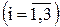 .
.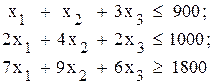
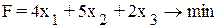 .
. , поэтому простые алгебраические преобразования не приведут к желаемому результату. В таких случаях необходимо воспользоваться методом искусственного базиса. Для этого следует перейти от ограничений-неравенств к ограничениям-равенствам путем введения в неравенства дополнительных переменных
, поэтому простые алгебраические преобразования не приведут к желаемому результату. В таких случаях необходимо воспользоваться методом искусственного базиса. Для этого следует перейти от ограничений-неравенств к ограничениям-равенствам путем введения в неравенства дополнительных переменных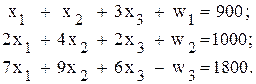
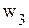 будет отрицательной, что недопустимо. Согласно методу искусственного базиса в ограничение-равенство с переменной
будет отрицательной, что недопустимо. Согласно методу искусственного базиса в ограничение-равенство с переменной 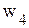
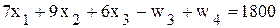 .
.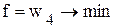 .
.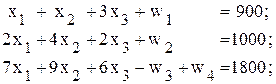
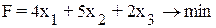 ;
; .
.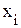 и
и 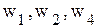 будут базисными. Однако целевая функция не может содержать базисные переменные, поэтому
будут базисными. Однако целевая функция не может содержать базисные переменные, поэтому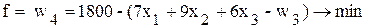 .
. ;
;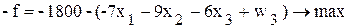 .
.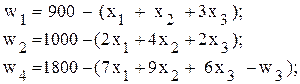
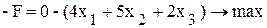 ;
;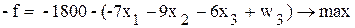 .
.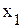
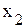 ↑
↑
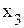
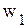
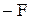

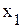
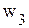
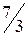
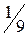
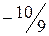
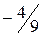
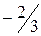
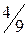
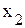
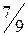
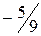
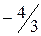
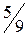
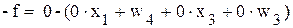 ,
,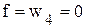 .
.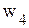 , добавленную в ограничение-равенство, и получить начальное допустимое базисное решение, имеющее вид
, добавленную в ограничение-равенство, и получить начальное допустимое базисное решение, имеющее вид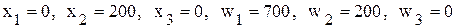 .
.


