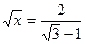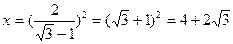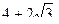Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Иррациональные уравнения и неравенства
Введение Иррациональными уравнениями и неравенствами называются такие уравнения и неравенства, в которых присутствует знак радикала (
Определение 1 Задача Е1 называется эквивалентной (равносильной) задаче Е2, если множества их решений совпадают. В записи это обозначается так: Е1 Е2 В дальнейшем изложении мы будем рассматривать уравнения и неравенства, содержащие знак квадратного корня. Корни более высоких степеней встречаются на экзаменах крайне редко и только в специально подобранных задачах.
Напомним определение квадратного корня:
Определение 2 (1) (2) (
Замечание 1 Наличие буквы a в правой части второго равенства показывает, что подкоренное выражение не может быть отрицательным. Поскольку это знают все старшеклассники, то указывать на это в тех местах, где есть знак радикала, не следует. Вообще, обращать внимание на область определения той или иной функции, входящей в исходную задачу, в процессе преобразований задачи нужно не раньше, чем тогда, когда исчез знак этой функции. Например, наличие знаменателя предполагает, что он не нуль, и указывать на это следует в том месте, где мы от него избавились (в исходной-то задаче он был!).
Часть 1. Иррациональные уравнения.
§1 Основное уравнение
Это уравнение вида:
(1)
Утверждение 1 Имеет место эквивалентность:
(A)
Доказательство: Пусть число x а левая часть неотрицательна по определению, то имеет место неравенство (C).
Таким образом, каждое решение исходного уравнения является также и решением системы. Обратно, пусть x Если x Пусть и равенство (A) опять имеет место.
Замечание 2 Предостерегаем читателя от распространённого заблуждения: “нуль, умноженный на что угодно, даёт нуль”. (Операция “нуль умножить на Ивана Семёновича”, точно так же, как Поэтому в общем случае имеет место эквивалентный переход:
Замечание 3 Поскольку правая часть уравнения (B) представляет полный квадрат, то все его решения x
Замечание 4 Переход к следствию с последующей проверкой равенства (A), часто не оправдан из-за затруднений, возникающих при этой проверке.
§ 2 Примеры записи решений основной задачи
Пример 1. Р ешить уравнение: Решение:
Ответ:
Пример 2 Решить уравнение:
Решение:
Ответ: Пример 3 Решить уравнение:
Решение:
Ответ:
Пример 4 Решить уравнение: Решение:
Ответ: решений нет.
Пример 5 Решить уравнение: Решение:
Ответ: Задачи с двумя радикалами Наиболее распространёнными задачами этого типа являются следующие три:
(I)
(II)
(III)
Утверждение 2 Имеют место эквивалентности:
Замечание 5 Тождественный переход Однако в некоторых случаях этого делать не надо. Например, левая и правая части тождества Здесь слева Возможен другой путь:
и задача сводится к основному типу.
Доказательства мы предоставляем читателю в качестве самостоятельной работы.
§ 4 Примеры записи решений задач с двумя радикалами
Пример 6. Решить уравнение: Решение:
Пример 7. Решить уравнение:
Решение:
Ответ:
Пример 8. Решить уравнение: Решение
Ответ: Пример 9. Решить уравнение:
Решение:
Ответ:
Пример 10. Решить уравнение:
Решение:
Ответ:
(этот пример показывает, что в стандартной задаче решение может быть более простым, если учесть специфику данной конкретной задачи).
|
||||||||
|
Последнее изменение этой страницы: 2020-12-19; просмотров: 190; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.113.197 (0.082 с.) |
 ).Основной проблемой при решении такого рода задач является поиск кратчайшего пути, приводящего к более простой эквивалентной задаче, не содержащей радикалов.
).Основной проблемой при решении такого рода задач является поиск кратчайшего пути, приводящего к более простой эквивалентной задаче, не содержащей радикалов.
 ³ 0 (квадратный корень обозначает неотрицательное число)
³ 0 (квадратный корень обозначает неотрицательное число)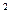 = a (и такое, что его квадрат равен подкоренному выражению)
= a (и такое, что его квадрат равен подкоренному выражению)


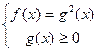
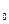 является решением уравнения (A). Тогда, во-первых, из равенства чисел следует равенство их квадратов, т.е. для x
является решением уравнения (A). Тогда, во-первых, из равенства чисел следует равенство их квадратов, т.е. для x 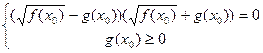
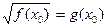 , то всё доказано.
, то всё доказано.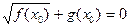 и g(x
и g(x 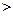 0, тогда очевидно, что
0, тогда очевидно, что 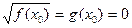 ,
,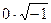 , не определены!).
, не определены!).
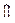
 и D
и D 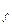 -- области определения соответствующих функций,
а квадратная скобка обозначает совокупность, решением которой
является объединение решений её составляющих
-- области определения соответствующих функций,
а квадратная скобка обозначает совокупность, решением которой
является объединение решений её составляющих
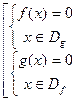
 , и соответствующая проверка – пустая трата времени.
, и соответствующая проверка – пустая трата времени.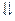
 ,
,
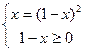
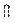

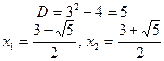
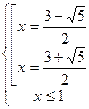
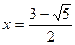
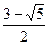 .
.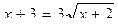

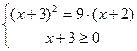
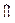


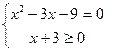
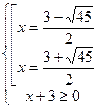
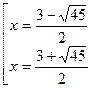
 ,
,  .
. 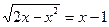
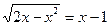
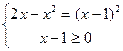

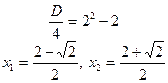

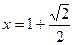
 .
.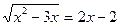
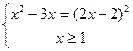
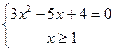
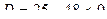


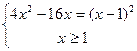 Из теоремы Виета видно, что корни разных знаков.
Из теоремы Виета видно, что корни разных знаков.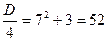

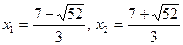
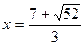
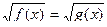
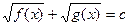
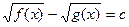 , где
, где  - положительная константа.
- положительная константа.
 (или
(или 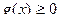 , смотря, что проще) (ИУ 2)
, смотря, что проще) (ИУ 2)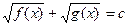
 (ИУ 3.1)
(ИУ 3.1)
 , выполняемый слева направо, может расширить область определения задачи, из-за чего могут возникнуть посторонние корни. После такой замены следует восстановить ограничения
, выполняемый слева направо, может расширить область определения задачи, из-за чего могут возникнуть посторонние корни. После такой замены следует восстановить ограничения  ,
,  , имеют одинаковые области определения.
, имеют одинаковые области определения. , а справа
, а справа 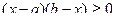 , что то же самое.
, что то же самое.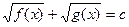

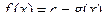
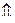 (ИУ 3.2)
(ИУ 3.2)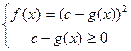 ,
,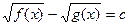
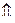 (ИУ 4)
(ИУ 4)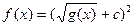
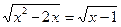
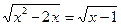
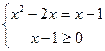

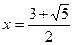 Ответ:
Ответ:  .
.
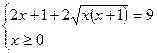


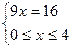
 =
= 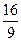
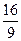 .
.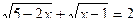
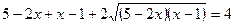

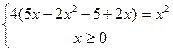
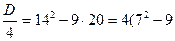
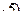
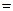


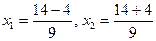
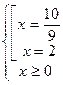
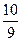 ;
; 
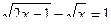
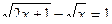

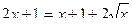

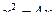
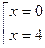
 ;
;