Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение иррациональных уравненийСтр 1 из 7Следующая ⇒
Иррациональные уравнения. · Дурягина Валентина Николаевна, учитель математики Разделы: Преподавание математики Цели и задачи урока: Развивающие: Активизация мыслительной деятельности учащихся. Развитие познавательной активности и интереса к предмета. Воспитательные: Развитие культуры математической речи при ответах на вопросы и при объяснении решения уравнений; зрительной памяти; внимательности и самостоятельности; творческого отношения к выполнению заданий. Тип урока: Комбинированный. Формы методы и педагогические приемы: Фронтальная беседа, комментирование решений, устная проверочная работа, создание проблемных ситуаций, дифференцированная самостоятельная работа, подготовка и защита плакатов с методами решения иррациональных уравнений, работа с учебником. Оборудование: Магнитная доска, откидные доски, тетради, чистые листы, раздаточный материал (карточки с вариантами самостоятельной работ), плакаты с решениями иррациональных уравнений методом возведения в степень и замена переменных. План урока: 1. Организационный момент. Содержание урока. Работа с учебником: Учитель предлагает еще раз вспомнить понятие иррационального уравнения, примеры их решения (образцы в тексте), какими методами решали уравнения, какими понятиями при этом пользовались. Устный опрос в форме фронтальной беседы с целью проверки теоретических знаний: 1. Что такое уравнение? [Уравнение – это равенство двух алгебраических выражений]. 2. Что называется корнем уравнения? [Корнем уравнения называется, то значение переменной, при котором данное уравнение обращается в верное равенство]. 3. Что значит решить уравнение? [Решить уравнение – значит найти все его корни или доказать, что уравнение не имеет корней]. 4. Какие уравнения называются равносильными? [Два уравнения равносильны на множестве, если они имеют одни и те же корни из этого множества или не имеют корней на данном множестве]. 5. Какие уравнения называют иррациональными уравнениями? [Уравнения, содержащие переменную под знаком корня, называют иррациональными уравнениями].
6. Каковы методы решения иррациональных уравнений? [Часто используемый прием решения иррациональных уравнений – это возведение в степень (чаще всего возведение в квадрат). Другой метод – это метод замены переменных]. Защита плакатов.
Плакаты ученики делали дома на ватмане. Прикрепив плакат на магнитной доске учащиеся поочередно защищают свой метод решения иррациональных уравнений. Учащиеся задают вопросы докладчикам. Почему при решении уравнения на плакате №1 в 1 способе поставлен всюду знак
Во втором способе решения областью определения уравнения является множество чисел х 2. Почему при решение уравнения [ Так как все переходы при решении уравнения равносильны, то проверка корня не требуется]. Устная проверочная работа: На откидной доске учителем заранее записаны задания
Решение иррациональных уравнений на доске и в тетрадях.
На доске заранее учителем записаны следующие уравнения: 1. 2. 3. 4. Решение: Обе части уравнения возведем в квадрат и учтем область определения уравнения, при этом будем использовать знак
Ответ: 15 Вопрос учителя: Почему область определения уравнения записана не равенством х>11, а не х 2. Решение: Так как под знаком Пусть
Проверка: х=3, х=-8, Ответ: 3; -8. 3. Решение: Решим уравнение методом замены переменных. Пусть
Возвращаемся к переменной х.
3х+1=16 (3х-6=9 Проверка: 4 + 3 =7 (верно) Ответ: х=5. Комментарий учителя: некоторые учащиеся выбрали другой способ решения – возведения в квадрат, но он приводит к громоздким вычислениям, поэтому метод замены в данном уравнении более удачный. 4. Решение: Уединим
Д=192-4*84=25; х1= Проверка: х=12, х=7, х=12 – посторонний корень Ответ: х=7. 5. Решение: Будем использовать метод возведения обеих частей уравнения в нечетную третью степень, при котором посторонние корни не появляются.
Ответ: 10 6. Решение: Обе части уравнения возведем в квадрат и запишем область определения данного уравнения.
Ответ: -1 На данном этапе урока наблюдалась ошибка при возведении двучлена в квадрат. Например: (х-7)2=х2-49, а надо (х-7)2=х2-14х+49. При выборе метода решения в уравнении №4 многие предпочитают метод возведения в квадрат, что не рационально. Самостоятельная работа. Каждый учащийся получает карточку с одним из трех вариантов. Первый вариант для слабоуспевающих учеников, второй и третий для более успешных учащихся. Вариант 1
Вариант 2
Вариант 3
Иррациональные уравнения СОДЕРЖАНИЕ. Введение. Из истории Равносильные уравнения. Следствия уравнений. Уравнений. Заключение Список используемой литературы ВВЕДЕНИЕ В школьном курсе алгебры рассматриваются различные виды уравнений – линейные, квадратные, биквадратные, кубические, рациональные, с параметрами, иррациональные и другие. Данная курсовая работа посвящена иррациональным уравнениям, методам их решения. Кроме того, в работе введены понятия уравнений следствий и равносильных уравнений, а также приведены примеры задач, математическими моделями которых служат иррациональные уравнения. В данной работе содержится небольшая историческая справка, посвященная введению иррациональных чисел
ИЗ ИСТОРИИ Термин “рациональное” (число) происходит от латиноамериканского слова ratio – отношение, которое является переводом греческого слова “логос”в отличие от рациональных чисел, числа, выражающие отношение несоизмеримых величин, были названы еще в древности иррациональными, т.е. нерациональными (по-гречески “алогос”) правда, первоначально термины “рациональный” и “иррациональный” относились не к числам, а к соизмеримым и соответственно не соизмеримым величинам, которые пифагорейцы называли выразимыми и невыразимыми, Теодор Киренский же симметричными и ассимметричными. В V-VI вв. римские авторы Капелла и Кассиодор переводили эти термины на латынь словами rationalis и irrationalis. Термин “соизмеримый” (commensurabilis) ввел в первой половине VI в. другой римский автор- Боэций. Древнегреческие математики классической эпохи пользовались только рациональными числами (вернее целыми, дробными и положительными). В своих “Началах” Евклид излагает учение об иррациональностях чисто геометрически. Математики Индии, Ближнего и Среднего Востока, развивая алгебру, тригонометрию и астрономию, не могли обойтись без иррациональных величин, которые, однако, длительное время не признавали за числа. Греки называли иррациональную величину, например, корень из квадратного числа, “алогос” – невыразимое словами, а позже европейские переводчики с арабского на латынь перевели это слово латинским словом surdus – глухой. В Европе термин surdus- глухой впервые появился в середине XII в. у Герарда Кремонского, известного переводчика математических прозведений с арабского на латынь, затем у итальянского математика Леонардо Фабоначчи и других европейских математиков, вплоть до XVIII в. Правда уже в XVI в. Отдельные ученые, в первую очередь итальянский математик Рафаэль Бомбелли и нидерландский математик Симон Стевин считали понятие иррационального числа равноправным с понятием рационального числа. Стевин писал: “Мы приходим к выводу, что не существует никаких абсурдных, иррациональных, неправильных, необъяснимых или глухих чисел, но что среди чисел существует такое совершенство и согласие, что нам надо размышлять дни и ночи над их удивительной закономерностью.”
Еще до Бомбелли и Стевина многие ученые стран Среднего Востока в своих трудах употребляли иррациональные числа как полноправные объекты алгебры. Более того, комментируя “Начала” Евклида и исследуя общую теорию отношения Евдокса, Омар Хайям уже в начале XII в. теоретически расширяет понятие числа до положительного действительного числа. В том же направлении много было сделано крупнейшим математиком XIII в. ат-Туси. Математики и астрономы Ближнего и Среднего Востока вслед за астрономами древнего Вавилона и эллинистической эпохи широко пользовались шестидесятеричными дробями, арифметические действия с которыми они называли “арифметикой астрономов”. По аналогии с шестидесятеричными дробями самаркандский ученый XV в. ал-Каши в работе “Ключ арифметики” ввел десятичные дроби которыми он пользовался для повышения точности извлечения корней. Независимо от него по такому же пути шел открывший в 1585 г. десятичные дроби в Европе Симон Стевин, который в своих “приложениях к алгебре” (1594 г.) показал, что десятичные дроби можно использовать для бесконечно близкого приближения к действительному числу. Таким образом, уже в XVI в. зародилась идея о том, что естественным аппаратом для введения и обоснования понятия иррационального числа являются десятичные дроби. Появление “Геометрии” Декарта облегчило понимание связи между измерением любых отрезков (и геометрических величин вообще) и необходимости расширения понятия рационального числа. На числовой оси иррациональные числа, как и рациональные, изображаются точками. Это геометрическое толкование позволило лучше понять природу иррациональных чисел и способствовало их признанию. В современных учебных руководствах основа определения иррационального числа опирается на идеи ал-Каши, Стевина и Декарта об измерении отрезков и о неограниченном приближении к искомому числу с помощью бесконечных десятичных дробей. Однако обоснованием свойств действительных чисел и полная теория их была разработана лишь в XIX в. Что и требовалось доказать. Рассмотрим уравнение
ОДЗ этого уравнения {х ≠ 1, х ≠ -3} Мы знаем, что дробь равна нулю в том случае, когда ее числитель равен нулю, т.е. хІ+х–2=0, а знаменатель не равен 0. Решая уравнение хІ+х–2=0, находим корни х1=1, х2 = –2. Но число 1 не входит в ОДЗ данного уравнения и значит, исходное уравнение имеет один кореньх=-2.
пусть даны два уравнения: f1 (x) = g1 (x) (3) f2 (x) = g2 (x) (4) И потому отброшен.
ОДЗ которого {х № -2},
В тех случаях, когда в результате преобразований произошел переход от исходного уравнения к уравнению, не являющемуся его следствием, возможна потеря корней. Например, уравнение (х+1)(х+3)= х+1 (5) Имеет два корня. Действительно, перенося все члены уравнения в левую часть и вынося х+1 за скобки, получим (х+1)(х+2)=0, откуда находим х1=-1, х2=-2. Если же обе части уравнения (5) разделить (“сократить”) на х+1, то получим уравнение х+3=1, имеющее один корень х=-2. В результате такого преобразования корень х=-1 потерян. Поэтому делить обе части уравнения на выражение, содержащее переменную, можно лишь в том случае, когда это выражение отлично от нуля. Пример №1 Решить уравнение
далее последовательно имеем: 5х – 16 = хІ - 4х + 4 хІ - 4х + 4 – 5х + 16 = 0 хІ - 9х + 20 = 0
Значения – корни уравнения. Ответ: 4; 5. Пример №2 Решить уравнение:
(2) Решение: Преобразуем уравнение к виду:
Ответ: -1 Решить уравнение Решение: Ответ: 1. Сопряжённое выражению
Так как То уравнение (1) примет вид: Или Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, а другой при этом известен. Тогда x1=0.Остаётся решить уравнение: (2) Ответ: 4. ЗАКЛЮЧЕНИЕ Итак, уравнения, которые содержат переменную под знаком корня, называются иррациональными. Иррациональные уравнения решаются в основном возведением обеих частей уравнения в квадрат (или n-ую степень) или введением новой переменной. Кроме того, пользуются и искусственными приемами решения иррациональных уравнений. СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ. 1) А.Г.Мордкович. Алгебра 8 класс. Учебник для общеобразовательных учреждений - Москва: Издательство “Мнемозина”, 1999. Иррациональные уравнения
Иногда математическая модель реальной ситуации представляет собой иррациональное уравнение, мы с этим уже встречались (см. замечание к примеру 3 из § 22). Поэтому нам следует научиться решать хотя бы простейшие иррациональные уравнения. Рассмотрим иррациональное уравнение
Это — и корень уравнения 2х + 1 = 9, и заданного иррационального уравнения. Метод возведения в квадрат технически несложен, но иногда приводит к неприятностям. Рассмотрим, например, иррациональное уравнение
2x-4x = -7 +5; -2x = -2; х = 1. Но значение х - 1, будучи корнем рационального уравнения 2x - 5 = 4x - 7, не является корнем заданного иррационального уравнения. Почему? Подставив 1 вместо х в заданное иррациональное уравнение, получим
Подставив значение 2 вместо х в заданное иррациональное уравнение, получим
Это неверно. Подставив значение - 19 вместо х в заданное иррациональное уравнение, получим
Это также неверно. Каков же вывод? Оба найденные значения — посторонние корни. Иными словами, заданное иррациональное уравнение, как и предыдущее, не имеет корней. Посторонний корень — не новое для вас понятие, посторонние корни уже встречались при решении рациональных уравнений, обнаружить их помогает проверка. Для иррациональных уравнений проверка — обязательный этап решения уравнения, который поможет обнаружить посторонние корни, если они есть, и отбросить их (обычно говорят «отсеять»). Итак, иррациональное уравнение решают методом возведения обеих его частей в квадрат; решив полученное в итоге рациональное уравнение, надо обязательно сделать проверку, отсеяв возможные посторонние корни. Используя этот вывод, рассмотрим несколько примеров. Пример 1. Решить уравнение
Решение. Возведем обе части уравнения (1) в квадрат:
Пример 2. Решить уравнение
2x2 + 8* + 16 = (44 - 2х)2. Далее имеем 2х2 + 8х + 16 = 1936 - 176x + 4x2;
это, очевидно, неверное равенство, поскольку в его правой части содержится отрицательное число, а в левой — положительное число. Значит, х = 80 — посторонний корень для данного уравнения. Подставив х = 12 в заданное иррациональное уравнение, получим
т. е.. Ответ: 12.
Далее находим: Проверка. Подставив значение x = 14 в уравнение (2), получим Подставив значение x = -1 в уравнение (2), получим О т в е т: - 1. Пример 4. Решить уравнение Решение. Конечно, можно решить это уравнение по той же схеме, которую мы применяли в предыдущих примерах: переписать уравнение в виде Ответ: 1. Завершим этот параграф достаточно серьезным теоретическим разговором. Дело в следующем. Вы уже накопили некоторый опыт в решении различных уравнений: линейных, квадратных, рациональных, иррациональных. Вы знаете, что при решении уравнений выполняют различные преобразования, например: член уравнения переносят из одной части уравнения в другую с противоположным знаком; обе части уравнения умножают или делят на одно и то же отличное от нуля число; освобождаются от знаменателя, т. е. заменяют уравнение Конечно, вы обратили внимание на то, что в результате некоторых преобразований могли появиться посторонние корни, а потому приходилось быть бдительными: проверять все найденные корни. Вот мы и попытаемся сейчас осмыслить все это с теоретической точки зрения. Определение. Два уравнения f (x) = g (x) и r(x) = s (х) называют равносильными, если они имеют одинаковые корни (или, в частности, если оба уравнения не имеют корней). Обычно при решении уравнения стараются заменить данное уравнение более простым, но равносильным ему. Такую замену называют равносильным преобразованием уравнения. Равносильными преобразованиями уравнения являются следующие преобразования: 1. Перенос членов уравнения из одной части уравнения в другую с противоположными знаками. Например, замена уравнения 2х + 5 = 7х - 8 уравнением 2х - 7х = - 8 - 5 есть равносильное преобразование уравнения. Это значит, что уравнения 2х + 5 = 7х -8 и 2х - 7х = -8 - 5 равносильны. 2. Умножение или деление обеих частей уравнения на одно и то же отличное от нуля число. Например, замена уравнения 0,5x2 - 0,3x = 2 уравнением 5х2 - Зх = 20 (обе части уравнения умножили почленно на 10) есть равносильное преобразование уравнения. Неравносильными преобразованиями уравнения являются следующие преобразования: 1. Освобождение от знаменателей, содержащих переменные. Примеры приводить не будем, так как их было достаточно много в этом параграфе. Если в процессе решения уравнения применялось одно из указанных неравносильных преобразований, то все найденные корни надо проверить подстановкой в исходное уравнение, поскольку среди них могут оказаться посторонние корни. Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил.
онлайн библиотека с учебниками и книгами, планы конспектов уроков по математике, задания по математике 8 класса скачать
Иррациональные, показательные и логарифмические уравнения Иррациональные уравнения. Иррациональными называются уравнения, содержащие неизвестную величину под знаком корня. Таковы, например, уравнения
Во многих случаях, применяя однократно или многократно возведение в степень обеих частей уравнения, удается свести иррациональное уравнение к алгебраическому уравнению той или иной степени (являющемуся следствием исходного уравнения). Так как при возведении уравнения в степень могут появиться посторонние решения, то, решив алгебраическое уравнение, к которому мы привели данное иррациональное уравнение, следует найденные корни проверить подстановкой в исходное уравнение и сохранить лишь те, которые ему удовлетворяют, а остальные — посторонние — отбросить. При решении иррациональных уравнений мы ограничиваемся только их действительными корнями; все корни четной степени в записи уравнений понимаются в арифметическом смысле. Рассмотрим некоторые типичные примеры иррациональных уравнений. А. У равнения, содержащие неизвестную под знаком квадратного корня. Если данное уравнение содержит только один квадратный корень, под знаком которого имеется неизвестная Пример 1. Решить уравнение Решение. Уединяем корень в левой части уравнения;
Возводим полученное равенство в квадрат:
Находим корни этого уравнения:
Проверка показывает, что лишь Если в уравнение входит два и более корня, содержащих х, то возведение в квадрат приходится повторять несколько раз. Пример 2. Решить следующие уравнения:
Решение, а) Возводим обе части уравнения в квадрат:
Уединяем корень:
Полученное уравнение снова возводим в квадрат:
После преобразований получаем для
решаем его:
Подстановкой в исходное уравнение убеждаемся в том, что б) Пример
Справа стоит произведение суммы на разность, т. е. разность квадратов. Отсюда
или
В левой части данного уравнения стояла сумма квадратных корней; в левой части полученного теперь уравнения стоит разность тех же корней. Запишем данное и полученное уравнения:
Взяв сумму этих уравнений, получаем
или
Возведем в квадрат последнее уравнение и после упрощений получим
Отсюда находим
Здесь уже под знаком радикала мы имеем квадратные трехчлены. Решение. Умножаем уравнение на выражение, сопряженное с его левой частью:
отсюда
Вычтем последнее уравнение из данного:
Отсюда
или
Возводим это уравнение в квадрат:
Отсюда
Из последнего уравнения находим Б. У равнения, содержащие корни третьей степени. Системы иррациональных уравнений. Ограничимся отдельными примерами таких уравнений и систем. Пример 4. Решить уравнение
Решение. Покажем два способа решения уравнения (70.1). Первый способ. Возведем обе части данного уравнения в куб (см. формулу (20.8)):
(здесь мы заменили сумму кубических корней числом 4, пользуясь уравнением Итак, имеем
или
т. е., после упрощений,
|
|||||||||||||||
|
Последнее изменение этой страницы: 2020-12-19; просмотров: 1524; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.66.206 (0.252 с.) |
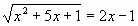 Решение: I способ: Возведем обе части уравнения в квадрат.
Решение: I способ: Возведем обе части уравнения в квадрат.
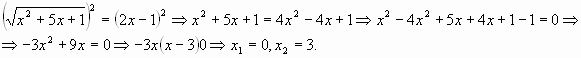 Проверка: 1) х=0, то
Проверка: 1) х=0, то  (неверно);
2) х=3, то
(неверно);
2) х=3, то 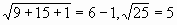 (верно)
II способ:
(верно)
II способ:
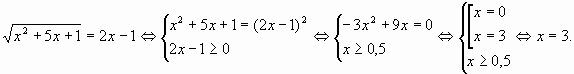 Ответ: 3.
№2 Метод замены переменных.
Решить уравнение
Ответ: 3.
№2 Метод замены переменных.
Решить уравнение 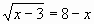 Решение: Пусть t=
Решение: Пусть t= 
 Значит, 2=
Значит, 2= 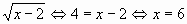 Ответ: 6
Ответ: 6
 (следствия), и в другом способе знак
(следствия), и в другом способе знак  (равносильности)?[ Уравнение х2+5х+1=(2х-1)2 имеет 2 корня – х2=0, х2=3, а уравнение
(равносильности)?[ Уравнение х2+5х+1=(2х-1)2 имеет 2 корня – х2=0, х2=3, а уравнение 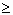 0,5, а число х=3 принадлежит этому множеству, значит все переходы, равносильны.
0,5, а число х=3 принадлежит этому множеству, значит все переходы, равносильны.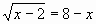 не делали проверку корня?
не делали проверку корня?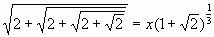 иррациональным?
2. Какие из чисел 5; 0;-3 являются корнями уравнений?
а)
иррациональным?
2. Какие из чисел 5; 0;-3 являются корнями уравнений?
а) 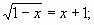 [x=0]
б)
[x=0]
б)  [x=5]
3. Решите уравнения
1)
[x=5]
3. Решите уравнения
1)  [x=83]
2)
[x=83]
2) 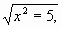 [x=±5]
3)
[x=±5]
3) 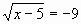 [O]
4)
[O]
4) 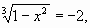 [x=±3]
5) х-6
[x=±3]
5) х-6 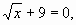 [x=9]
6)
[x=9]
6) 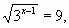 [x=5]
7)
[x=5]
7)  lg([-12)=0, [O]
lg([-12)=0, [O]
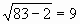 (верно).
х2=25
(верно).
х2=25 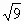 +9=0.
Возведем обе части уравнения в квадрат и решим показательное уравнение
3х-1=34; х=5.
Если
+9=0.
Возведем обе части уравнения в квадрат и решим показательное уравнение
3х-1=34; х=5.
Если 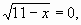 то х=11, тогда lg(-1), чего быть не может, т.к. логарифмы отрицательных чисел не определены.
то х=11, тогда lg(-1), чего быть не может, т.к. логарифмы отрицательных чисел не определены.
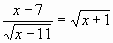 ;
;
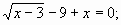
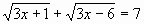 ;
;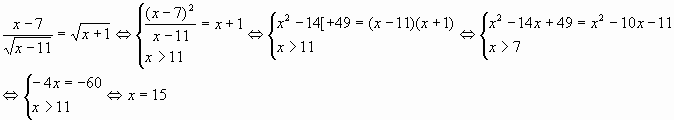
 11? [При х=11 знаменателем дроби равен 0, а на 0 делить нельзя].
11? [При х=11 знаменателем дроби равен 0, а на 0 делить нельзя].
 записаны одинаковые выражения, то удобно применить метод замены.
записаны одинаковые выражения, то удобно применить метод замены. тогда
тогда 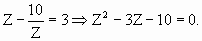 Решая квадратное уравнение относительно переменной Z, получим Z1=5; Z2=-2. Учитывая область определения уравнения х2+5х+1>0, заметим, что при Z=5 25+25+1>0 (да), а при Z=-2 4-10+1>0 (неверно), то Z2=-2 посторонний корень. Вернемся к переменной х,
Решая квадратное уравнение относительно переменной Z, получим Z1=5; Z2=-2. Учитывая область определения уравнения х2+5х+1>0, заметим, что при Z=5 25+25+1>0 (да), а при Z=-2 4-10+1>0 (неверно), то Z2=-2 посторонний корень. Вернемся к переменной х, х1=3; х2=-8.
х1=3; х2=-8.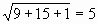 (верно)
(верно)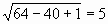 (верно)
(верно)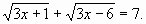
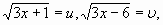 тогда
тогда 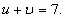 Чтобы составить вопрос уравнения с переменными
Чтобы составить вопрос уравнения с переменными  и
и 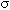 , возведем обе части уравнений
, возведем обе части уравнений 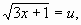
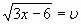 в квадрат 3х+1=u2 и 3х-6=
в квадрат 3х+1=u2 и 3х-6= 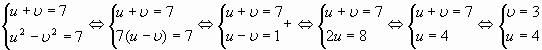
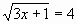 ; (или
; (или 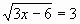 )
)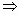 3х=15
3х=15 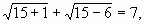

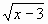 в левой части уравнения и возведем обе части уравнения в квадрат.
в левой части уравнения и возведем обе части уравнения в квадрат.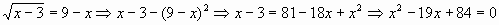
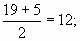 х2= 7.
х2= 7.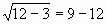 (неверно)
(неверно) (верно)
(верно)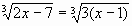

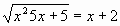

 б)
б) 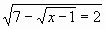 в) х-
в) х- 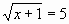
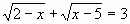 б)
б)  в)
в) 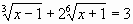


 В этом случае говорят, что уравнение хІ+х–2=0, есть следствие уравнения
В этом случае говорят, что уравнение хІ+х–2=0, есть следствие уравнения Иногда посторонние корни могут появиться и при тождественных преобразованиях, если они приводят к изменению ОДЗ уравнения. Например, после приведения подобных членов в левой части уравнения
Иногда посторонние корни могут появиться и при тождественных преобразованиях, если они приводят к изменению ОДЗ уравнения. Например, после приведения подобных членов в левой части уравнения
 получим уравнение следствие хІ-4=0 имеющее два корня х1 = 2, х2 = -2корень х2 = -2 – посторонний, так как не входит в ОДЗ исходного уравнения.
получим уравнение следствие хІ-4=0 имеющее два корня х1 = 2, х2 = -2корень х2 = -2 – посторонний, так как не входит в ОДЗ исходного уравнения. Возведем обе части уравнения (1) в квадрат:
Возведем обе части уравнения (1) в квадрат: Проверка: Подставивх=5 в уравнение (1), получим – верное равенство. Подставив х= 4 в уравнение (1), получим – верное равенство. Значит оба найденных
Проверка: Подставивх=5 в уравнение (1), получим – верное равенство. Подставив х= 4 в уравнение (1), получим – верное равенство. Значит оба найденных
 и применим метод возведения в квадрат:
и применим метод возведения в квадрат:

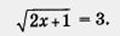
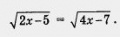

 . Как же можно говорить о выполнении числового равенства, если и в левой и в правой его части содержатся выражения, не имеющие смысла? В подобных случаях говорят: х = 1 — посторонний корень для заданного иррационального уравнения. Получается, что заданное иррациональное уравнение не имеет корней.
. Как же можно говорить о выполнении числового равенства, если и в левой и в правой его части содержатся выражения, не имеющие смысла? В подобных случаях говорят: х = 1 — посторонний корень для заданного иррационального уравнения. Получается, что заданное иррациональное уравнение не имеет корней. 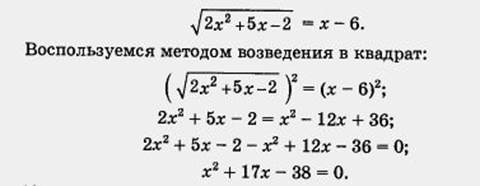




 — верное равенство. Подставив х = 4 в уравнение (1), получим
— верное равенство. Подставив х = 4 в уравнение (1), получим 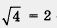 — верное равенство. Значит, оба найденные значения — корни уравнения (1).
— верное равенство. Значит, оба найденные значения — корни уравнения (1).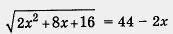
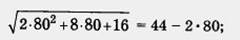
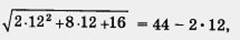
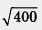 = 20, — верное равенство. Следовательно, х = 12 — корень данного уравнения.
= 20, — верное равенство. Следовательно, х = 12 — корень данного уравнения.
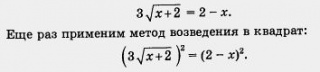
 — неверное равенство, значит, x = 14 — посторонний корень.
— неверное равенство, значит, x = 14 — посторонний корень. — верное равенство. Поэтому x = - 1 — корень уравнения (2).
— верное равенство. Поэтому x = - 1 — корень уравнения (2).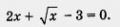
 возвести обе части этого уравнения в квадрат, решить полученное рациональное уравнение и проверить найденные корни подстановкой их в
возвести обе части этого уравнения в квадрат, решить полученное рациональное уравнение и проверить найденные корни подстановкой их в 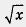 . Тогда получим 2у2 + у - 3 = 0 — квадратное уравнение относительно переменной у. Найдем его корни: у1 = 1, у2 = -
. Тогда получим 2у2 + у - 3 = 0 — квадратное уравнение относительно переменной у. Найдем его корни: у1 = 1, у2 = - 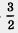 . Таким образом, задача свелась к решению двух
. Таким образом, задача свелась к решению двух 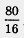
 принимает только неотрицательные значения).
принимает только неотрицательные значения).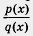 = 0 уравнением р (х) = 0; обе части уравнения возводят в квадрат.
= 0 уравнением р (х) = 0; обе части уравнения возводят в квадрат.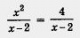 уравнением х2 = 4 есть неравносильное преобразование уравнения. Дело в том, что уравнение х2 = 4 имеет два корня: 2 и - 2, а заданному уравнению значение х = 2 удовлетворять не может (знаменатель обращается в нуль). В подобных случаях мы говорили так: х = 2 — посторонний корень. 2. Возведение обеих частей уравнения в квадрат.
уравнением х2 = 4 есть неравносильное преобразование уравнения. Дело в том, что уравнение х2 = 4 имеет два корня: 2 и - 2, а заданному уравнению значение х = 2 удовлетворять не может (знаменатель обращается в нуль). В подобных случаях мы говорили так: х = 2 — посторонний корень. 2. Возведение обеих частей уравнения в квадрат.
 то следует этот корень уединить, т. е. поместить в одной части уравнения, а все другие члены перенести в другую часть. После возведения в квадрат обеих частей уравнения мы уже освободимся от иррациональности и получим алгебраическое уравнение для
то следует этот корень уединить, т. е. поместить в одной части уравнения, а все другие члены перенести в другую часть. После возведения в квадрат обеих частей уравнения мы уже освободимся от иррациональности и получим алгебраическое уравнение для 
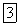 .
.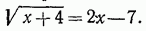

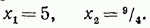
 удовлетворяет исходному уравнению.
удовлетворяет исходному уравнению.

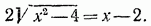

 следующее квадратное уравнение:
следующее квадратное уравнение:

 есть его корень, а
есть его корень, а  является для него посторонним корнем.
является для него посторонним корнем. 
 можно решить тем же методом, каким был решен пример а). Однако, воспользовавшись тем, что правая часть данного уравнения не содержит неизвестной величины, поступим иначе. Умножим уравнение на выражение, сопряженное с его левой частью; получим
можно решить тем же методом, каким был решен пример а). Однако, воспользовавшись тем, что правая часть данного уравнения не содержит неизвестной величины, поступим иначе. Умножим уравнение на выражение, сопряженное с его левой частью; получим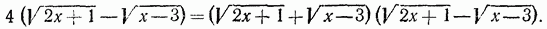
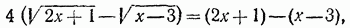
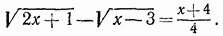
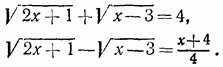
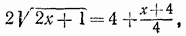
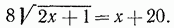
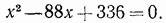
 . Проверкой убеждаемся в том, что корнем данного уравнения служит только число
. Проверкой убеждаемся в том, что корнем данного уравнения служит только число  . Пример 3. Решить уравнение
. Пример 3. Решить уравнение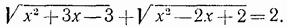
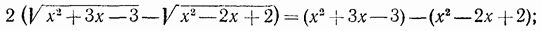
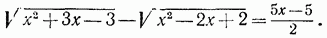

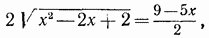


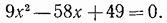
 . Проверкой убеждаемся, что корнем данного уравнения служит только число х = 1.
. Проверкой убеждаемся, что корнем данного уравнения служит только число х = 1.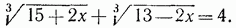

 ).
).