Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
А.П.Савин. Энциклопедический словарь юного математика – Москва: Издательство “Педагогика”, 1989.
Transcript · 1. Иррациональные уравнениялекция 1. · 2. Теоретический материал · 3. Теоретический материал · 4. Теоретический материал · 5. Теоретический материал · 6. Простейшие иррациональные уравнения: · 7. Методы решения иррациональных уравнений
· 8. Методы решения иррациональных уравнений · 9. Методы решения иррациональных уравнений · 10. Методы решения иррациональных уравнений · 11. Методы решения иррациональных уравнений · 12. Методы решения иррациональных уравнений · 13. Методы решения иррациональных уравнений · 14. Методы решения иррациональных уравнений · 15. Методы решения иррациональных уравнений · 16. Методы решения иррациональных уравнений · 17. Источники:
Иррациональные уравнения
Иногда математическая модель реальной ситуации представляет собой иррациональное уравнение, мы с этим уже встречались (см. замечание к примеру 3 из § 22). Поэтому нам следует научиться решать хотя бы простейшие иррациональные уравнения. Рассмотрим иррациональное уравнение
Это — и корень уравнения 2х + 1 = 9, и заданного иррационального уравнения. Метод возведения в квадрат технически несложен, но иногда приводит к неприятностям. Рассмотрим, например, иррациональное уравнение
2x-4x = -7 +5; -2x = -2; х = 1. Но значение х - 1, будучи корнем рационального уравнения 2x - 5 = 4x - 7, не является корнем заданного иррационального уравнения. Почему? Подставив 1 вместо х в заданное иррациональное уравнение, получим
Подставив значение 2 вместо х в заданное иррациональное уравнение, получим
Это неверно. Подставив значение - 19 вместо х в заданное иррациональное уравнение, получим
Это также неверно. Каков же вывод? Оба найденные значения — посторонние корни. Иными словами, заданное иррациональное уравнение, как и предыдущее, не имеет корней. Посторонний корень — не новое для вас понятие, посторонние корни уже встречались при решении рациональных уравнений, обнаружить их помогает проверка. Для иррациональных уравнений проверка — обязательный этап решения уравнения, который поможет обнаружить посторонние корни, если они есть, и отбросить их (обычно говорят «отсеять»). Итак, иррациональное уравнение решают методом возведения обеих его частей в квадрат; решив полученное в итоге рациональное уравнение, надо обязательно сделать проверку, отсеяв возможные посторонние корни. Используя этот вывод, рассмотрим несколько примеров. Пример 1. Решить уравнение
Решение. Возведем обе части уравнения (1) в квадрат:
Пример 2. Решить уравнение
2x2 + 8* + 16 = (44 - 2х)2. Далее имеем 2х2 + 8х + 16 = 1936 - 176x + 4x2;
это, очевидно, неверное равенство, поскольку в его правой части содержится отрицательное число, а в левой — положительное число. Значит, х = 80 — посторонний корень для данного уравнения. Подставив х = 12 в заданное иррациональное уравнение, получим
т. е.. Ответ: 12.
Далее находим: Проверка. Подставив значение x = 14 в уравнение (2), получим Подставив значение x = -1 в уравнение (2), получим О т в е т: - 1. Пример 4. Решить уравнение Решение. Конечно, можно решить это уравнение по той же схеме, которую мы применяли в предыдущих примерах: переписать уравнение в виде Ответ: 1. Завершим этот параграф достаточно серьезным теоретическим разговором. Дело в следующем. Вы уже накопили некоторый опыт в решении различных уравнений: линейных, квадратных, рациональных, иррациональных. Вы знаете, что при решении уравнений выполняют различные преобразования, например: член уравнения переносят из одной части уравнения в другую с противоположным знаком; обе части уравнения умножают или делят на одно и то же отличное от нуля число; освобождаются от знаменателя, т. е. заменяют уравнение Конечно, вы обратили внимание на то, что в результате некоторых преобразований могли появиться посторонние корни, а потому приходилось быть бдительными: проверять все найденные корни. Вот мы и попытаемся сейчас осмыслить все это с теоретической точки зрения. Определение. Два уравнения f (x) = g (x) и r(x) = s (х) называют равносильными, если они имеют одинаковые корни (или, в частности, если оба уравнения не имеют корней). Обычно при решении уравнения стараются заменить данное уравнение более простым, но равносильным ему. Такую замену называют равносильным преобразованием уравнения. Равносильными преобразованиями уравнения являются следующие преобразования: 1. Перенос членов уравнения из одной части уравнения в другую с противоположными знаками.
Например, замена уравнения 2х + 5 = 7х - 8 уравнением 2х - 7х = - 8 - 5 есть равносильное преобразование уравнения. Это значит, что уравнения 2х + 5 = 7х -8 и 2х - 7х = -8 - 5 равносильны. 2. Умножение или деление обеих частей уравнения на одно и то же отличное от нуля число. Например, замена уравнения 0,5x2 - 0,3x = 2 уравнением 5х2 - Зх = 20 (обе части уравнения умножили почленно на 10) есть равносильное преобразование уравнения. Неравносильными преобразованиями уравнения являются следующие преобразования: 1. Освобождение от знаменателей, содержащих переменные. Примеры приводить не будем, так как их было достаточно много в этом параграфе. Если в процессе решения уравнения применялось одно из указанных неравносильных преобразований, то все найденные корни надо проверить подстановкой в исходное уравнение, поскольку среди них могут оказаться посторонние корни. Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил.
онлайн библиотека с учебниками и книгами, планы конспектов уроков по математике, задания по математике 8 класса скачать
Иррациональные, показательные и логарифмические уравнения Иррациональные уравнения. Иррациональными называются уравнения, содержащие неизвестную величину под знаком корня. Таковы, например, уравнения
Во многих случаях, применяя однократно или многократно возведение в степень обеих частей уравнения, удается свести иррациональное уравнение к алгебраическому уравнению той или иной степени (являющемуся следствием исходного уравнения). Так как при возведении уравнения в степень могут появиться посторонние решения, то, решив алгебраическое уравнение, к которому мы привели данное иррациональное уравнение, следует найденные корни проверить подстановкой в исходное уравнение и сохранить лишь те, которые ему удовлетворяют, а остальные — посторонние — отбросить. При решении иррациональных уравнений мы ограничиваемся только их действительными корнями; все корни четной степени в записи уравнений понимаются в арифметическом смысле. Рассмотрим некоторые типичные примеры иррациональных уравнений. А. У равнения, содержащие неизвестную под знаком квадратного корня. Если данное уравнение содержит только один квадратный корень, под знаком которого имеется неизвестная Пример 1. Решить уравнение
Решение. Уединяем корень в левой части уравнения;
Возводим полученное равенство в квадрат:
Находим корни этого уравнения:
Проверка показывает, что лишь Если в уравнение входит два и более корня, содержащих х, то возведение в квадрат приходится повторять несколько раз. Пример 2. Решить следующие уравнения:
Решение, а) Возводим обе части уравнения в квадрат:
Уединяем корень:
Полученное уравнение снова возводим в квадрат:
После преобразований получаем для
решаем его:
Подстановкой в исходное уравнение убеждаемся в том, что б) Пример
Справа стоит произведение суммы на разность, т. е. разность квадратов. Отсюда
или
В левой части данного уравнения стояла сумма квадратных корней; в левой части полученного теперь уравнения стоит разность тех же корней. Запишем данное и полученное уравнения:
Взяв сумму этих уравнений, получаем
или
Возведем в квадрат последнее уравнение и после упрощений получим
Отсюда находим
Здесь уже под знаком радикала мы имеем квадратные трехчлены. Решение. Умножаем уравнение на выражение, сопряженное с его левой частью:
отсюда
Вычтем последнее уравнение из данного:
Отсюда
или
Возводим это уравнение в квадрат:
Отсюда
Из последнего уравнения находим Б. У равнения, содержащие корни третьей степени. Системы иррациональных уравнений. Ограничимся отдельными примерами таких уравнений и систем. Пример 4. Решить уравнение
Решение. Покажем два способа решения уравнения (70.1). Первый способ. Возведем обе части данного уравнения в куб (см. формулу (20.8)):
(здесь мы заменили сумму кубических корней числом 4, пользуясь уравнением Итак, имеем
или
т. е., после упрощений,
откуда Второй способ. Положим
Уравнение (70.1) запишется в виде
Разделив первое уравнение системы почленно на второе, найдем
и уже легко решим систему вида
Ее решения: Из равенства
Рассмотрим теперь примеры решения систем уравнений с двумя неизвестными, из которых по крайней мере одно уравнение иррациональное. Пример 5. Решить систему уравнений
Решение. Обозначим
откуда
Теперь из второго уравнения системы находим Если взять Пример 6. Решить систему уравнений
Решение. Возведя в квадрат первое уравнение, получим
С помощью второго уравнения системы найдем
Последнее уравнение является квадратным относительно Уху. Из него находим только положительное значение
Решив эту систему, найдем, что пара чисел (1, 1) служит единственным решением и ее, и исходной системы.
|
|||||||||
|
Последнее изменение этой страницы: 2020-12-19; просмотров: 118; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.103.8 (0.106 с.) |
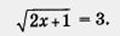
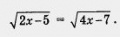

 . Как же можно говорить о выполнении числового равенства, если и в левой и в правой его части содержатся выражения, не имеющие смысла? В подобных случаях говорят: х = 1 — посторонний корень для заданного иррационального уравнения. Получается, что заданное иррациональное уравнение не имеет корней.
. Как же можно говорить о выполнении числового равенства, если и в левой и в правой его части содержатся выражения, не имеющие смысла? В подобных случаях говорят: х = 1 — посторонний корень для заданного иррационального уравнения. Получается, что заданное иррациональное уравнение не имеет корней. 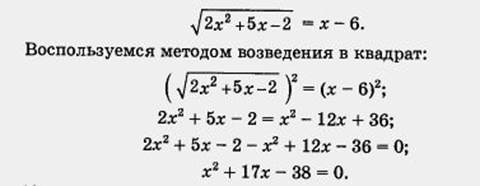




 — верное равенство. Подставив х = 4 в уравнение (1), получим
— верное равенство. Подставив х = 4 в уравнение (1), получим 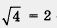 — верное равенство. Значит, оба найденные значения — корни уравнения (1).
— верное равенство. Значит, оба найденные значения — корни уравнения (1).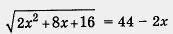
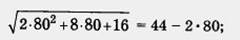
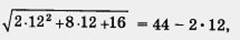
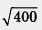 = 20, — верное равенство. Следовательно, х = 12 — корень данного уравнения.
= 20, — верное равенство. Следовательно, х = 12 — корень данного уравнения.
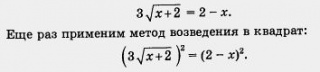
 — неверное равенство, значит, x = 14 — посторонний корень.
— неверное равенство, значит, x = 14 — посторонний корень. — верное равенство. Поэтому x = - 1 — корень уравнения (2).
— верное равенство. Поэтому x = - 1 — корень уравнения (2).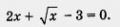
 возвести обе части этого уравнения в квадрат, решить полученное рациональное уравнение и проверить найденные корни подстановкой их в
возвести обе части этого уравнения в квадрат, решить полученное рациональное уравнение и проверить найденные корни подстановкой их в 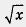 . Тогда получим 2у2 + у - 3 = 0 — квадратное уравнение относительно переменной у. Найдем его корни: у1 = 1, у2 = -
. Тогда получим 2у2 + у - 3 = 0 — квадратное уравнение относительно переменной у. Найдем его корни: у1 = 1, у2 = - 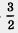 . Таким образом, задача свелась к решению двух
. Таким образом, задача свелась к решению двух 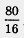
 принимает только неотрицательные значения).
принимает только неотрицательные значения).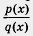 = 0 уравнением р (х) = 0; обе части уравнения возводят в квадрат.
= 0 уравнением р (х) = 0; обе части уравнения возводят в квадрат.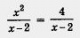 уравнением х2 = 4 есть неравносильное преобразование уравнения. Дело в том, что уравнение х2 = 4 имеет два корня: 2 и - 2, а заданному уравнению значение х = 2 удовлетворять не может (знаменатель обращается в нуль). В подобных случаях мы говорили так: х = 2 — посторонний корень. 2. Возведение обеих частей уравнения в квадрат.
уравнением х2 = 4 есть неравносильное преобразование уравнения. Дело в том, что уравнение х2 = 4 имеет два корня: 2 и - 2, а заданному уравнению значение х = 2 удовлетворять не может (знаменатель обращается в нуль). В подобных случаях мы говорили так: х = 2 — посторонний корень. 2. Возведение обеих частей уравнения в квадрат.
 то следует этот корень уединить, т. е. поместить в одной части уравнения, а все другие члены перенести в другую часть. После возведения в квадрат обеих частей уравнения мы уже освободимся от иррациональности и получим алгебраическое уравнение для
то следует этот корень уединить, т. е. поместить в одной части уравнения, а все другие члены перенести в другую часть. После возведения в квадрат обеих частей уравнения мы уже освободимся от иррациональности и получим алгебраическое уравнение для 
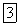 .
.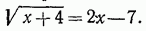

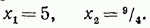
 удовлетворяет исходному уравнению.
удовлетворяет исходному уравнению.

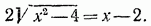

 следующее квадратное уравнение:
следующее квадратное уравнение:

 есть его корень, а
есть его корень, а  является для него посторонним корнем.
является для него посторонним корнем. 
 можно решить тем же методом, каким был решен пример а). Однако, воспользовавшись тем, что правая часть данного уравнения не содержит неизвестной величины, поступим иначе. Умножим уравнение на выражение, сопряженное с его левой частью; получим
можно решить тем же методом, каким был решен пример а). Однако, воспользовавшись тем, что правая часть данного уравнения не содержит неизвестной величины, поступим иначе. Умножим уравнение на выражение, сопряженное с его левой частью; получим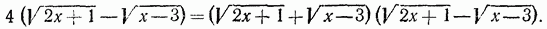
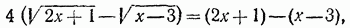
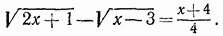
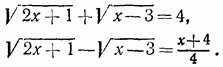
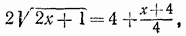
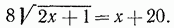
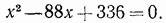
 . Проверкой убеждаемся в том, что корнем данного уравнения служит только число
. Проверкой убеждаемся в том, что корнем данного уравнения служит только число  . Пример 3. Решить уравнение
. Пример 3. Решить уравнение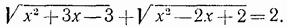
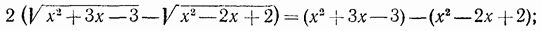
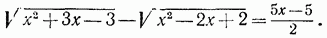

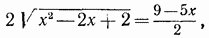


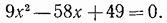
 . Проверкой убеждаемся, что корнем данного уравнения служит только число х = 1.
. Проверкой убеждаемся, что корнем данного уравнения служит только число х = 1.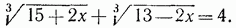

 ).
).
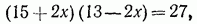
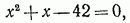
 Оба корня удовлетворяют исходному уравнению.
Оба корня удовлетворяют исходному уравнению.
 . Кроме того, видно что
. Кроме того, видно что  . От уравнения (70.1) мы перешли к системе
. От уравнения (70.1) мы перешли к системе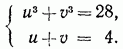
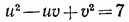
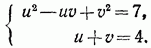
 .
. находим при
находим при  и
и  :
: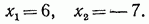
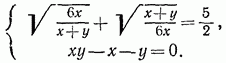
 . Это позволит первое уравнение системы записать в виде
. Это позволит первое уравнение системы записать в виде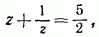
 . Взяв
. Взяв  , найдем
, найдем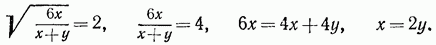
 Из корней этого неполного квадратного уравнения берем только
Из корней этого неполного квадратного уравнения берем только  (корень
(корень  отбрасываем; почему?). Отсюда
отбрасываем; почему?). Отсюда  .
. то получим
то получим  (читатель проведет все необходимые для этого выкладки самостоятельно). Итак, данная система имеет следующие решения:
(читатель проведет все необходимые для этого выкладки самостоятельно). Итак, данная система имеет следующие решения:  .
.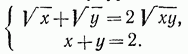
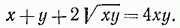
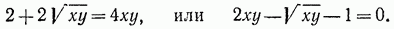
 откуда
откуда  , и данную систему тем самым сводим к системе
, и данную систему тем самым сводим к системе