
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Энтропия как мера неопределенности выбора
Ранее отмечалось, что факт получения информации всегда связан с уменьшением разнообразия или неопределенности. Рассмотрим источник информации, который может в каждый момент времени случайным образом принять из конечного множества возможных состояний. Такой источник называют дискретным источником информации. При этом принято говорить, что различные состояния реализуются вследствие выбора их источником. Каждому состоянию источника Для получения результата выбора источником
или
причём или Обе формы записи используются в дальнейшем на равных основаниях. Опираясь на эти сведения, введём сначала меру неопределенности выбора состояния источника. Её можно рассматривать и как меру количества информации, получаемой при полном устранении неопределенности относительно состояния источника. Мера должна удовлетворять ряду естественных условий. Одним из них является необходимость монотонного состояния возрастания с увеличением возможных состояний источника Ограничиваясь только этим условиям, за меру неопределенности можно было бы взять число состояний, предположив, что они равновероятны. Однако такая мера противоречит некоторым интуитивным представлениям. Например, при Если два независимых источника с числом равновероятных состояний
Это соотношение выполняется, если в качестве меры неопределенности источника с равновероятными состояниями и характеризующего его ансамбля
Тогда при Указанная мера была предложена американским ученым Р. Хартли в 1928 г. Основание логарифма не имеет принципиального значения и определяет только масштаб или единицу неопределенности. Так как современная информационная техника базируется на элементах, имеющих два устойчивых состояния, то обычно выбирают основание логарифма равным двум. При этом единица неопределенности называется двоичной единицей или битом и представляет собой неопределенность выбора из двух равновероятных событий (bit – сокращение от англ. binary digit – двоичная единица). Если основание логарифма выбрать равным десяти, то неопределенность получим в десятичных единицах на одно состояние (дитах). Предложенная мера позволяет решать определенные практические задачи. Однако она не получила широкого применения, поскольку была рассчитана на слишком грубую модель источника информации, которая приписывает всем его возможным состояниям одинаковую вероятность. Таким образом, степень неопределенности реализации состояния источника информации зависит не только от числа состояний, но и от вероятности этих состояний. При неравновероятных состояниях свобода выбора источника ограничивается, что должно приводить к уменьшению неопределенности. Если источник информации имеет, например, два возможных состояния с вероятностями 0,99 и 0,01, то неопределенность выбора у него значительно меньше, чем у источника, имеющего два равновероятных состояния. Действительно, в первом случае результат практически предрешён (реализация состояния, вероятность которого равна 0,99), а во втором случае неопределенность максимальная, поскольку никакого обоснованного предположения о результате выбора сделать нельзя. Отметим, что весьма малое изменение вероятностей состояний вызывает соответственно изменение неопределенности выбора.
Это позволяет сформулировать следующее требование к искомой мере неопределенности Наибольшее её значение должно достигаться при равенстве вероятностей всех её состояний. Кроме того, так как мера неопределенности связывается только с фактом выбора, а не с множеством конкретных значений наблюдаемых явлений, то Ещё одно условие состоит в том, что мера неопределенности не должна зависеть от пути выбора состояния в ансамбле. Выбор может быть как непосредственным, так и многоступенчатым. В последнем случае неопределенность выбора состояния складывается из неопределенности выбора группы состояний и неопределенностей выбора состояния в каждой группе, рассчитанных с учётом вероятности выбора данной группы:
где Мера неопределенности выбора дискретным источником состояния из ансамбля
где К. Шенноном высказано утверждение, а советским ученым Л. Я. Хинчиным математически строго доказано, что это единственный функционал, удовлетворяющий сформулированным условиям. Если вновь ориентироваться на измерение неопределенности в двоичных единицах, то основание логарифма следует принять равным двум. Примем также
Предложенная мера была названа энтропией не случайно. Дело в том, что формальная структура выражения (36.5) совпадает с энтропией физической системы, определенной ранее Больцманом. Согласно второму закону термодинамики энтропия
где Так как
Совпадение имеет глубокий физический смысл, так как в обоих случаях величина Рассмотрим взаимосвязь меры К. Шеннона с мерой Хартли. Если в источнике может быть реализовано
Будем теперь считать вероятности событий различными, а неопределенность, которая приходится на одно конкретное состояние источника, характеризовать по аналогии величиной
Это частная неопределенность представляет собой случайную величину, которая зависит от того, какое состояние источника в действительности реализуется. Усреднив по всему ансамблю
Следовательно, мера К. Шеннона является естественным обобщением меры Хартли на случай ансамбля с неравновероятными состояниями. Она позволяет учесть статистические свойства источника информации.
СВОЙСТВА ЭНТРОПИИ Рассмотрим основные свойства энтропии, обратив внимание на то, что сформулированные условия для меры неопределенности выполняются. 1.Энтропия является вещественной и неотрицательной величиной, так как для любого 2.Энтропия – величина ограниченная. Для слагаемых
Обозначив
3.Энтропия обращается в нуль лишь в том случае, если вероятность одного из состояний равна единице; тогда вероятности всех остальных состояний, естественно равны нулю. Это положение соответствует случаю, когда состояние источника полностью определенно. 4.Энтропия максимальна, когда все состояния равновероятны, что можно доказать методом неопределенных множителей Лагранжа:
5.Энтропия источника
График зависимости
Отметим, что энтропия непрерывно зависит от вероятностей отдельных состояний, что непосредственно вытекает из непрерывности функции 6.Энтропия объединения нескольких статистически независимых источников информации равна сумме энтропий исходных источников. Не теряя общности, ограничимся рассмотрением объединения, которое включает два источника информации В соответствии с определением энтропия объединения
Здесь В случае статистической независимости источников информации Тогда
Учитывая, что
получим
Соответственно для энтропии объединения нескольких независимых источников
В дальнейшем для придания общности получаемым результатам о неопределенности выбора будем говорить в основном применительно к математическим моделям источников информации в виде ансамблей. 7.Энтропия характеризует среднюю неопределенность выбора одного состояния из ансамбля. При её определении используют только вероятности состояний, полностью игнорируя их содержательную сторону. Поэтому энтропия не может служить средством решения любых задач, связанных с неопределенностью. Например, при использовании этой меры для оценки неопределенности действия лекарства, приводящего к полному выздоровлению больных в 90% и улучшению самочувствия в остальных 10% случаев, она получится такой же, как и у лекарства, вызывающего в 90% случаев смерть, а в 10% - ухудшение состояния больных. 8.Энтропия как мера неопределенности согласуется с экспериментальными данными, полученными при изучении психологических реакций человека, в частности реакции выбора. Установлено, что время безошибочной реакции на последовательность беспорядочно чередующихся равновероятных раздражителей (например, загорающихся лампочек) растёт с увеличением их числа так же, как энтропия. Это время характеризует неопределенность выбора одного раздражителя. Замена равновероятных раздражителей неравновероятными приводит к снижению среднего времени реакции настолько, насколько уменьшается энтропия.
|
||||||||
|
Последнее изменение этой страницы: 2020-12-19; просмотров: 240; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.121.214 (0.09 с.) |
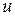 ставится в соответствие условное обозначение в виде знака (в частности, буквы) из алфавита данного источника:
ставится в соответствие условное обозначение в виде знака (в частности, буквы) из алфавита данного источника:  .
.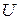 , т.е. полной совокупности состояний с вероятностями их появления, составляющими в сумме единицу:
, т.е. полной совокупности состояний с вероятностями их появления, составляющими в сумме единицу: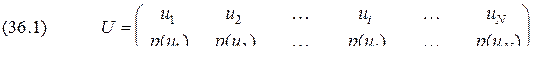
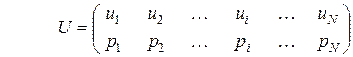
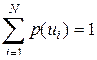
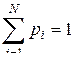 .
. , причём недопустимые состояния (состояния с вероятностями, равными нулю) не должны учитываться, так как они не меняют неопределенности.
, причём недопустимые состояния (состояния с вероятностями, равными нулю) не должны учитываться, так как они не меняют неопределенности. , когда неопределенность отсутствует, она давала бы значение, равное единице, кроме того, такая мера не отвечает требованию аддитивности, которое заключается в следующем.
, когда неопределенность отсутствует, она давала бы значение, равное единице, кроме того, такая мера не отвечает требованию аддитивности, которое заключается в следующем.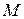 рассматривать как один источник, который одновременно реализует пары состояний
рассматривать как один источник, который одновременно реализует пары состояний  , то естественно предположить, что неопределенность объединенного источника должна равняться сумме неопределенностей исходных источников. Поскольку общее число состояний объединенного источника равно
, то естественно предположить, что неопределенность объединенного источника должна равняться сумме неопределенностей исходных источников. Поскольку общее число состояний объединенного источника равно  , то искомая функция должна удовлетворять условию
, то искомая функция должна удовлетворять условию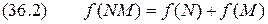 .
.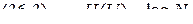
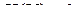 и требование аддитивности выполняется.
и требование аддитивности выполняется. : она должна быть непрерывной функцией вероятностей состояний источника
: она должна быть непрерывной функцией вероятностей состояний источника 
 с соблюдением условием
с соблюдением условием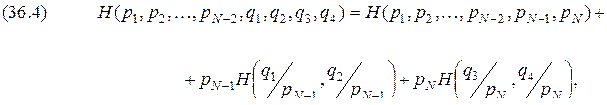
 и
и  вероятности состояний, которые образуют соответственно группы
вероятности состояний, которые образуют соответственно группы 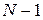 и
и 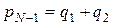 и
и 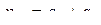 .
. ,
,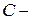 произвольное положительное число.
произвольное положительное число.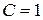 . Из (36.5)
. Из (36.5)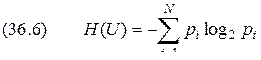 .
.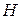 замкнутого пространства определяется выражением
замкнутого пространства определяется выражением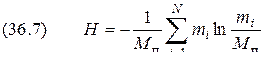 ,
,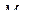 число молекул в данном пространстве;
число молекул в данном пространстве;  число молекул, обладающих скоростью
число молекул, обладающих скоростью 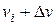 .
.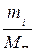 есть вероятность того, что молекула имеет скорость
есть вероятность того, что молекула имеет скорость 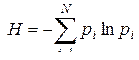 .
.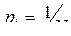 ,
, 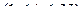 и неопределенность по Хартли, которая приходится на каждое состояние, выражается числом
и неопределенность по Хартли, которая приходится на каждое состояние, выражается числом .
.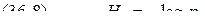 .
.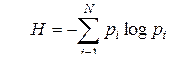 .
.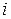
 изменяется в интервале от 0 до 1,
изменяется в интервале от 0 до 1, 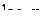 отрицателен и, следовательно,
отрицателен и, следовательно,  положительна.
положительна. ограниченность очевидна. Остаётся определить предел, к которому стремится слагаемое
ограниченность очевидна. Остаётся определить предел, к которому стремится слагаемое 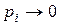 . Так как
. Так как 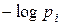 при этом неограниченно возрастает:
при этом неограниченно возрастает: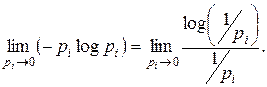
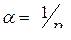 и воспользовавшись правилом Лопиталя, получим
и воспользовавшись правилом Лопиталя, получим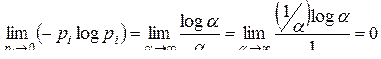 .
.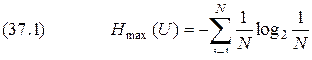 .
. и
и 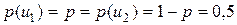 .
. в функции
в функции 
 приведен на рис.... При
приведен на рис.... При 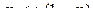 частная неопределенность, которая приходится на состояние
частная неопределенность, которая приходится на состояние  .
. . Под объединением двух источников
. Под объединением двух источников  , который характеризуется вероятностями
, который характеризуется вероятностями 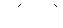 всех возможных состояний
всех возможных состояний 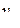 источника
источника 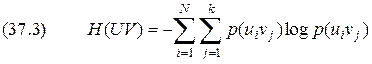 .
.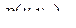 вероятность совместной реализации состояний
вероятность совместной реализации состояний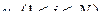 и
и  .
.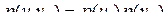 .
.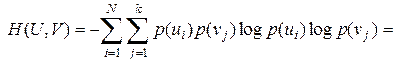
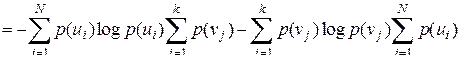 .
.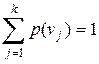 ,
, .
. имеем
имеем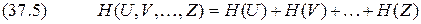 .
.


