
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Равномерная дискретизация. Теорема котельникова
Правило выбора предельного шага при равномерной дискретизации с использованием модели сигнала с ограниченным спектром в наиболее чёткой форме сформулировано и доказана академиком В.А. Котельниковым в виде теоремы, получившей в отечественной литературе его имя. Теорема Котельникова устанавливает принципиальную возможность полного восстановления детерминированной функции с ограниченным спектром по её отсчётам и указывает предельное значение интервала времени между отсчётами, при которой такое восстановление ещё возможно. Теорема. Функции
Физическая основа теоремы выявляется при рассмотрении связи между формой функции и шириной спектра. Только в том случае, когда спектр функции безграничен, её значений в сколь угодно близкие моменты времени могут изменяться произвольно (корреляционная связь между ними отсутствуют). Сокращение высокочастотной части спектра до граничной частоты При меньших граничных частотах
Рис.
Рис.
Рис.
Рис.
Рис. Поскольку значений этих функций в моменты времени Доказательство. Пусть функции
при Используя обратное преобразование Фурье с учётом соотношения (29.2), запишем
Для моментов времени
где функция
Функцию
где
Рис. Сравнивая (29.4) и (29.5), найдем
Выразим теперь
Поскольку суммирование ведётся как по положительным, так и по отрицательным числам
Подставив это значение в (29.3), определим значения исходной функции в любой момент времени
Учитывая сходимость ряда Фурье, изменим порядок суммирования и интегрирования
В полученном выражении вычислим интеграл
Подставив результат в формулу (29.7), окончательно получим
Итак, функция Так как при любых целых
то
Благодаря этому свойству значения функции Представление функции
Роль коэффициентов
Они называются функциями отсчётов. Графики этих функций при Каждая функция
относительно этого момента времени она симметрична.
где
Каждую функцию отсчёта можно рассматривать как реакцию (отклик) идеального фильтра нижних частот с ограниченной частотой Теорема Котельникова распространяется на непрерывный в среднеквадратическом смысле стационарный случайный процесс с ограниченным энергетическим спектром, т.е. Такой представляется суммой квазидетерминированных процессов, где роль ортогональных детерминированных функций выполняют функции отсчёта, а случайных коэффициентов - величины выборок:
где Таким образом, при указанных ограничениях случайный процесс полностью определяется счётным множеством случайных величин – координат процесса.
|
||||||
|
Последнее изменение этой страницы: 2020-12-19; просмотров: 142; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.66.206 (0.008 с.) |
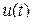 , допускающая преобразование Фурье и имеющая непрерывный спектр, ограниченный полосой частот от
, допускающая преобразование Фурье и имеющая непрерывный спектр, ограниченный полосой частот от 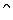 до
до 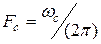 , полностью определяется дискретным рядом своих мгновенных значений, отсчитанных через интервал времени
, полностью определяется дискретным рядом своих мгновенных значений, отсчитанных через интервал времени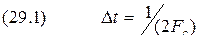 .
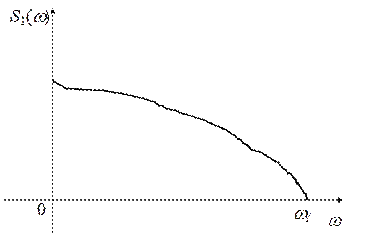
.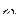 равнозначно устранению из временной функции выбросов, которые могли быть сформированы этими высокочастотными составляющими. Сокращение высокочастотной части спектра до граничной частоты
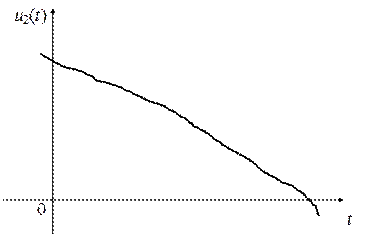
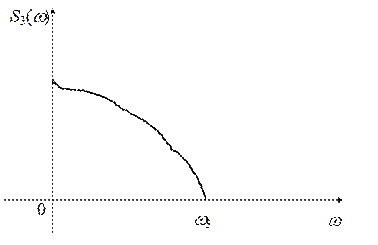
равнозначно устранению из временной функции выбросов, которые могли быть сформированы этими высокочастотными составляющими. Сокращение высокочастотной части спектра до граничной частоты 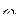 равнозначно устранению из временнóй функции выбросов, которые могли быть сформированы этими высокочастотными составляющими (рис.).
равнозначно устранению из временнóй функции выбросов, которые могли быть сформированы этими высокочастотными составляющими (рис.).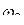 и
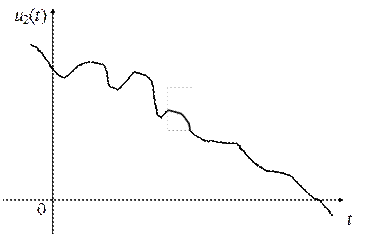
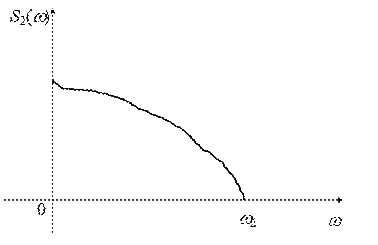
и 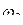 имеем более сглаженные функции времени.
имеем более сглаженные функции времени.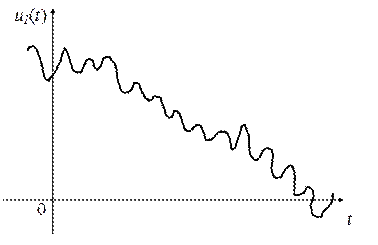
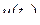 и
и 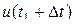 в пределах некоторого интервала
в пределах некоторого интервала 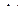 не могут изменяться существенно, можно ограничится значениями функции, взятыми через интервалы
не могут изменяться существенно, можно ограничится значениями функции, взятыми через интервалы 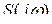 , причём
, причём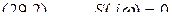
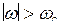 , где
, где 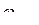 наибольшая частота спектра
наибольшая частота спектра 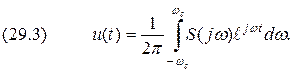
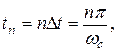
 -любое целое число,
-любое целое число,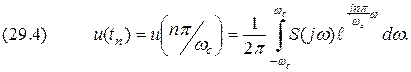
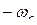 до
до 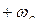 можно разложить в ряд Фурье по частотам, периодически продолжая её с периодом
можно разложить в ряд Фурье по частотам, периодически продолжая её с периодом 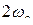 (рис.)
(рис.)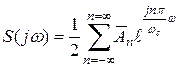
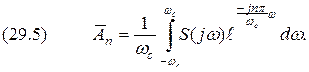

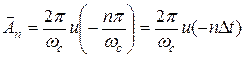 .
.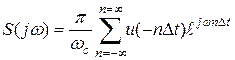 .
.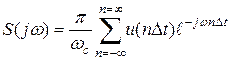 .
.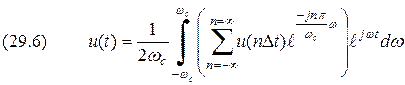 .
.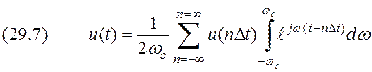 .
.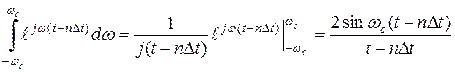 .
.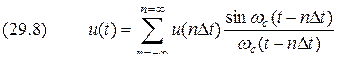 .
.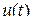 выражена через её дискретные значения, взятые в моменты времени
выражена через её дискретные значения, взятые в моменты времени 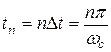 .
.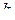 и
и  ,
,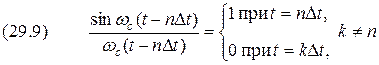 .
.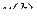 в моменты времени
в моменты времени 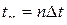 представляют собой нечто иное, как её отсчёты.
представляют собой нечто иное, как её отсчёты.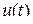 в виде ряда (29.8) (ряда Котельникова) является частным случаем разложения
в виде ряда (29.8) (ряда Котельникова) является частным случаем разложения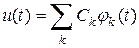 ,
, 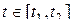 .
.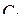 выполняют отсчёты
выполняют отсчёты 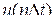 функции
функции 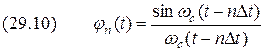 .
. и
и  приведены на рис.
приведены на рис.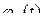 имеет неограниченную протяженность во времени и достигает своего наибольшего значения, равного единице, в момент времени
имеет неограниченную протяженность во времени и достигает своего наибольшего значения, равного единице, в момент времени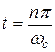
 ,
,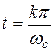 ,
, , функция обращается в нуль. Все функции ортогональны между собой на бесконечно большом промежутке времени, что легко проверятся путем вычисления интеграла
, функция обращается в нуль. Все функции ортогональны между собой на бесконечно большом промежутке времени, что легко проверятся путем вычисления интеграла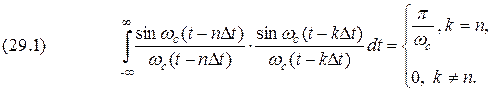
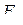 на дельта-функцию, которая приходит в момент времени
на дельта-функцию, которая приходит в момент времени 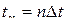 и которая имеет площадь равной
и которая имеет площадь равной 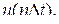
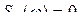 , при
, при 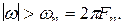
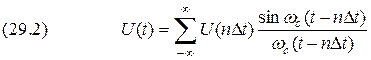 ,
,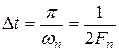 .
.


