
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
П. 53. Гиперкомплексные числовые системы. Кватернионы.
Если по аналогии перехода от действительных чисел к комплексным, удвоить размерность и образовать числа вида
При этом Получается антикоммутативная система с умножением:
Таблица умножения базисных элементов системы кватернионов.
Обратите внимание, что законы умножения в системе кватернионов
При умножении каждой пары получается следующий, если двигаться строго по часовой стрелке. Ещё обратите внимание, что мнимые единицы системы кватернионов подчиняются таким же законам, как векторное умножение в 3-мерном пространстве. Там тоже
Как и для комплексных чисел, здесь есть понятие «сопряжённый кватернион». Если Подробнее о том, почему получается
«Тело кватернионов». Кватернионы не образуют поле, так как умножение не коммутативно.
В конце пары: сам. работа 20 минут по алг. операциям
Дополнительно: 1. Установите изоморфизм групп: всех комплексных корней степени n из единицы и вычетов по модулю n. 2. Сколько существует различных матриц порядка n над полем вычетов 3. Привести пример обратимой матрицы порядка 2 над полем вычетов 4. Доказать, что многочлен 5. Решить систему уравнений 3 порядка в поле
6. Доказать, что алгебра матриц вида
изоморфна алгебре кватернионов. 7 Zn (n не простое) построить систему, не имеющую решений.
Практика 5 Линейные пространства. Задача 54. Являются ли линейно зависимыми функций: а) Решение. Если система функций ЛЗС, то очевидно, что система функций, состоящая из их производных, тоже ЛЗС.
Значит, мы можем проверить линейную зависимость системы функций с помощью определителя (если он тождественно равен 0, то ЛЗС). а) б)
Можно было рассуждать иначе, без определителя: Пусть в)
г) Задача 55. Являются ли линейно зависимыми функции:
Решение. Мы тоже могли бы решать с помощью определителя Вронского, однако рассмотрим и другой метод. Покажем, что линейная комбинация синуса и косинуса разных амплитуд равна косинусу с другой фазой (это будет впоследствии нужно и при изучении рядов Фурье).
Итак, третья функция линейно выражается через первые две, значит, система ЛЗС. Решить с помощью W(x) - дом задание.
Задача 56. Доказать, что пересечение подпространств является подпространством. Решение. Пусть Если элементы принадлежат пересечению, Тогда Задача 57. Доказать, что множество квадратных матриц 2 порядка образует 4-мерное пространство, найти какой-либо его базис.
Решение. Абелева группа (проверяли ранее) по сложению. Свойства умножения на константы: 1) 2) 3а) Базис: A= Всякая матрица может быть представлена в виде
Замечание. Пространство квадратных матриц порядка
Задача 58. 1) Множество многочленов степени не выше n образует линейное пространство (доказано в лекциях). Каковы его размерность, базис? 2) Доказать, что множество многочленов Решение. Базис
2)
Каждый многочлен можно разложить не только по основному, но и по другому базису. Так, например, Приближённое выражение произвольной функции с помощью степенных выражает формула Тейлора: - обобщение понятия касательной. Если рассмотреть только до 1-й степени, это уравнение касательной.
Если продолжить этот процесс до бесконечности, получили бы ряд Тейлора:
Задача 59. а) разложить многочлен б) разложить многочлен Решение. а)
Подставляем в формулу Тейлора.
Проверка: б)
Проверка:
Замечание. Множество всех многочленов степени ровно n не образует линейное пространство: если старший коэффициент одинаковый, то разность имеет степень меньше n.
- - - Перерыв - - -
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-17; просмотров: 144; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.105.239 (0.041 с.) |
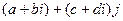 из пары комплексных чисел, где второе умножено ещё на какой-то объект
из пары комплексных чисел, где второе умножено ещё на какой-то объект  , то получается 4-мерная система с тремя мнимыми единицами и числами вида
, то получается 4-мерная система с тремя мнимыми единицами и числами вида  , которые называются кватернионами.
, которые называются кватернионами. это мы изначально называем произведение 1-й и 2-й мнимых единиц некоторой третьей мнимой единицей.
это мы изначально называем произведение 1-й и 2-й мнимых единиц некоторой третьей мнимой единицей. ,
,  ,
, 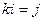 ,
,  ,
, 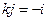 ,
, 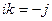 .
. . Умножение на 1 сохраняет любой объект неизменным.
. Умножение на 1 сохраняет любой объект неизменным.
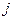
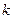
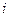







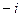
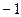
 ,
,  ,
,  легко запомнить, если представить с помощью цикла:
легко запомнить, если представить с помощью цикла:
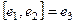 ,
,  ,
,  . Векторное произведение пары векторов есть общий перпендикуляр к ним, причём так чтобы получалась правоориентированная тройка. Векторное умножение было придумано Гамильтоном в 1843 году одновременно с системой кватернионов.
. Векторное произведение пары векторов есть общий перпендикуляр к ним, причём так чтобы получалась правоориентированная тройка. Векторное умножение было придумано Гамильтоном в 1843 году одновременно с системой кватернионов.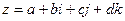 то
то 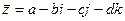 . При этом
. При этом 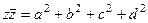 , то есть можно также ввести понятие модуля кватерниона:
, то есть можно также ввести понятие модуля кватерниона: 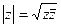 =
=  .
.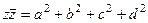 .
. =
= =
= но система антикоммутативна, т.е.
но система антикоммутативна, т.е. 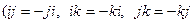 , поэтому все эти суммы в скобках равны 0, вот и остаётся
, поэтому все эти суммы в скобках равны 0, вот и остаётся 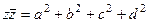 .
. ?
? 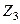 , найти обратную.
, найти обратную.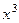 может иметь больше, чем 3 корня, в кольце вычетов. Найти пример кольца вычетов, в котором он имеет 4 различных корня.
может иметь больше, чем 3 корня, в кольце вычетов. Найти пример кольца вычетов, в котором он имеет 4 различных корня.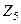 :
: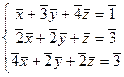

 . б)
. б) 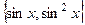 . в)
. в)  г)
г) 


 . Аналогичное верно для производных любого порядка. Далее, проведём решение с помощью определителя Вронского. На лекции мы уже ввели понятие определителя и изучили его свойства. В частности, определитель равен 0
. Аналогичное верно для производных любого порядка. Далее, проведём решение с помощью определителя Вронского. На лекции мы уже ввели понятие определителя и изучили его свойства. В частности, определитель равен 0  его строки (столбцы) образуют линейно зависимую систему векторов (см. свойство 9). Если мы достроим до квадратной матрицы, добавляя во 2-й строке производные, в 3-й вторые производные и т.д., то столбцы будут образовывать ЛЗС
его строки (столбцы) образуют линейно зависимую систему векторов (см. свойство 9). Если мы достроим до квадратной матрицы, добавляя во 2-й строке производные, в 3-й вторые производные и т.д., то столбцы будут образовывать ЛЗС  система функций ЛЗС. Такой определитель называется определителем Вронского:
система функций ЛЗС. Такой определитель называется определителем Вронского: .
.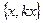 .
.  .
. .
.  =
= 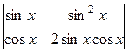 =
=  =
= 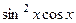 , не равно тождественно нулевой функции, система линейно-независима, ЛНС.
, не равно тождественно нулевой функции, система линейно-независима, ЛНС. , тогда было бы тождественно
, тогда было бы тождественно 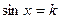 , что невозможно, поэтому система ЛНС.
, что невозможно, поэтому система ЛНС.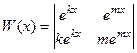 =
= 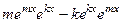 =
=  , при
, при 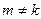 эта функция не равна тождественно 0. Система ЛНС.
эта функция не равна тождественно 0. Система ЛНС.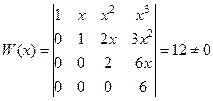 . Система ЛНС.
. Система ЛНС. .
. =
= 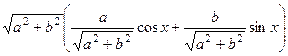 =
=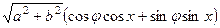 =
= 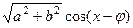 .
.  являются подпространствами
являются подпространствами  .
.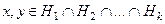 , то они принадлежат любому из
, то они принадлежат любому из 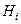 . Но каждое
. Но каждое  ,
, 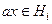
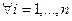 .
.  ,
, 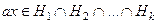 .
. .
.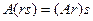
 3б)
3б)  .
. , B=
, B=  , C=
, C=  , D=
, D= 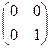 .
.  .
.  имеет размерность
имеет размерность  , пространство прямоугольных матриц размера
, пространство прямоугольных матриц размера 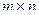 - размерность
- размерность  .
.  также является базисом.
также является базисом. .
. 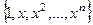 . Размерность n+1. Линейную независимость этой системы можно проверить с помощью определителя:
. Размерность n+1. Линейную независимость этой системы можно проверить с помощью определителя: 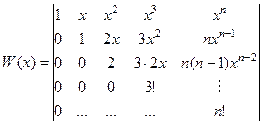 =
=  .
.  =
=
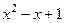 =
=  =
=  .
. 
 Для многочлена, начиная с некоторого порядка, производные станут 0, поэтому ряд конечный, и формула Тейлора задаёт не приближённо, а точно. В то же время, это способ задать многочлен по другому основанию.
Для многочлена, начиная с некоторого порядка, производные станут 0, поэтому ряд конечный, и формула Тейлора задаёт не приближённо, а точно. В то же время, это способ задать многочлен по другому основанию. по степеням
по степеням  .
.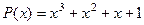 по степеням
по степеням 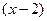 .
.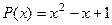
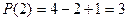




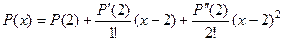 =
= 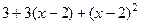 .
. =
=  =
= 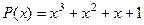

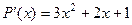
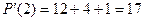
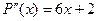
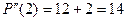

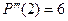
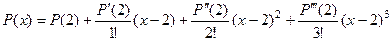 =
=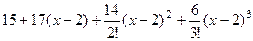 =
= 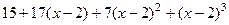 .
. 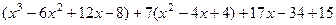 =
= =
= 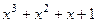 .
. 


