Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дискретная случайная величина.
Закон распределения случайной дискретной величины - связывает между собой значения случайной величины и вероятности принятия случайной величиной ее значений. Он может быть записан в форме таблицы:
Соответствие между отдельными возможными значениями и их вероятностями называется законом распределения дискретной случайной величины. Как и в случае функциональной зависимости, этот закон можно задать таблицей, аналитически (формулой) и графически. В случае табличного задания закона распределения дискретной случайной величины соответствующая таблица состоит из двух строк — первая указывает возможные значения, а вторая — их вероятности:
Поскольку в одном испытании случайная величина принимает только одно возможное значение, то события Х=х1, Х=х2 -..., Х=хп образуют полную группу, т.е. сумма их вероятностей равна единице: p 1 + p 2 + …+ pn = 1. Если множество возможных значений X дискретной случайной величины бесконечно, то соответствующий ряд вероятностей сходится и его сумма равна единице: p 1 +p2 +…+ p n +…= 1. Пример 1. В денежной лотерее на 100 билетов разыгрывается один выигрыш в 20 р., два выигрыша по 10 р. и 10 выигрышей по 1 р. Найти закон распределения случайной величины X возможного выигрыша на один билет. Решение. Возможные значения X: x 1 =20, х2 =10, х3=1, х4 =0. Соответственно их вероятности равны: X 20 10 1 0 Р 0,01 0,02 0,1 0,87. Пример 2. Партия из 8 изделий содержит 5 стандартных. Наудачу отбираются 3 изделия. Составить таблицу закона распределения числа стандартных изделий среди отобранных. Решение. Случайная величина X — число стандартных деталей среди отобранных — может принимать 4 возможных значения: 0, 1, 2 и 3. Вероятность нахождения к стандартных изделий среди трех отобранных определяется формулой
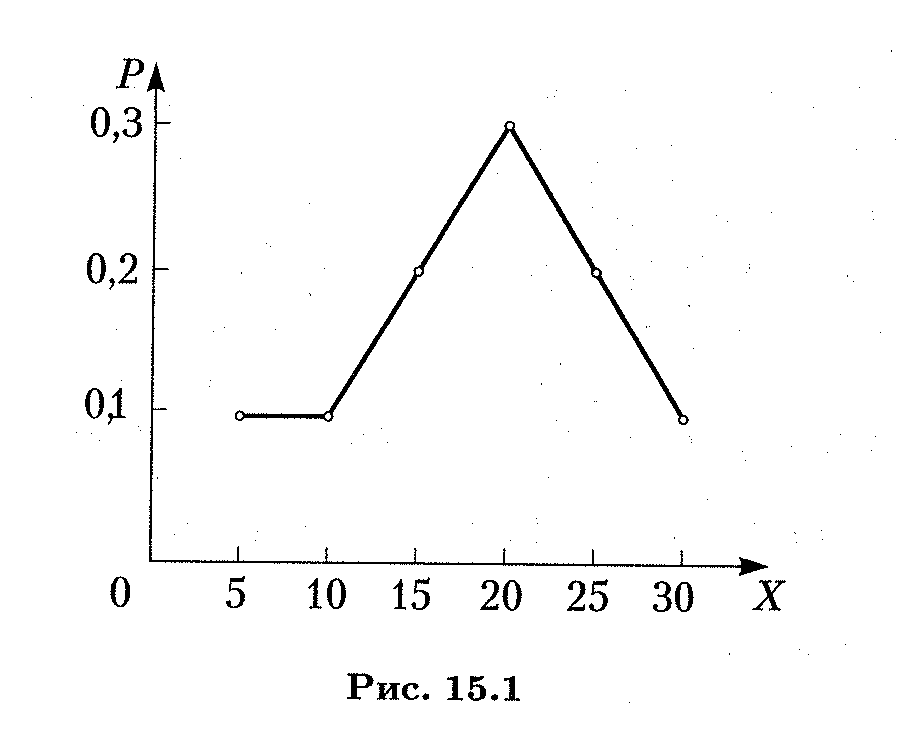
Варьируя значения к от 0 до 3, получаем искомое распределение: X 0 1 2 3 Р 0,0179 0,2679 0,5357 0,1785. Пример 3. Вероятностный прогноз для величины X — процентного изменения стоимости акций по отношению к их текущему курсу в течение шести месяцев — дан в виде закона распределения: X 5 10 15 20 25 30 Р 0,1 0,1 0,2 0,3 0,2 0,1.
Закон распределения дискретной случайной величины можно изобразить графически, соединив в прямоугольной системе координат ХО P точки (х i,р i) отрезками прямых. Так, на рис. 15.1 показан закон распределения из примера 3. Такая фигура называет ся многоугольником распределения.
Основные законы распределения случайных величин Биномиальное распределение Пусть производится п независимых испытаний и в каждом из них событие А может либо появиться, либо не появиться. Пусть также вероятность р появления события А в каждом испытании постоянна (см. раздел 14.5). В качестве дискретной случайной величины X рассмотрим число появления события А в этих п испытаниях. Очевидно, что х1 =0, х2=1, х3 =2,..., хп+1=п. Вероятности этих возможных значений к даются формулой Бернулли (см. формулу (14.16)):
где q = 1 - р — вероятность противоположного события (не появление события А в одном испытании). Формула (15.2) представляет собой аналитическую форму закона распределения случайной величины (числа появления события А в п независимых испытаниях), который называется биномиальным. Этот закон получил свое название потому, что правая часть в (15.2) представляет собой общий член разложения бинома Ньютона (14.2). Таким образом, табличная форма биномиального закона с учетом формулы (15.2) имеет вид
Можно показать, что сумма всех вероятностей второй отроки этой таблицы равна единице, т.е.
Пример 4 Банк выдает 5 кредитов. Вероятность невозврата, кредита равна 0,2 для каждого из заемщиков. Составить таблицу закона распределения количества заемщиков, не вернувших кредит по окончании срока кредитования. Решение. Примем за А событие невозврата кредита. Так как заемщики действуют независимо, то выдачу 5 кредитов можно считать за 5 независимых событий. Вероятность невозврата к кредитов из 5 описывается биномиальным распределением (15.2), где р = 0,2, q = 0,8, к принимает значения от нуля до 5. Искомая таблица закона распределения составляется, согласно (15.3), при n = 5: X 5 4 3 2 1 0 Р (0,2)5 5(0,2)40,8 10 (0,2)3(0,8)2 10(0,2)2(0,8)3 5(0,2)(0,8)4 (0,8)5,
или окончательно: X 5 4 3 2 1 0 Р 0,00032 0,0064 0,0512 0,2048 0,4096 0,32768.
Распределение Пуассона Пусть в каждом из п производимых испытаний вероятность появления события А равна р. Как мы знаем, для определения вероятности к появлений события А используется формула Бернулли (15.2); при больших п пользуются асимптотической формулой Лапласа (14.17). Однако эта формула плохо подходит для случая, когда р мало. Для случая малых значений р и больших значений п используется асимптотическая формула Пуассона, эта формула выведена при важном допущении, что произведение пр является постоянной величиной, т.е. пр = λ. Тогда вероятность того, что событие А наступит ровно к раз, дается формулой, которая представляет собой закон распределения Пуассона вероятностей массовых и редких (маловероятных) событий.
Пример 5. На базу отправлено 10 000 изделий. Вероятность того, что изделие в пути получит повреждение, равна 0,0003. Найти вероятность того, что на базу прибудут 4 поврежденных изделия. Решение. По условию задачи п = 10 000, р = 0,0003, к = 4. Находим λ, а затем по формуле (15.4) и искомую вероятность:
λ = пр= 10000•0,0003 = 3,
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 149; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.35.81 (0.006 с.) |
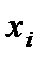
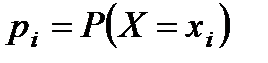
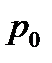
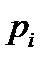
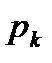
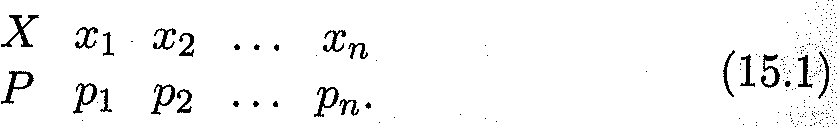 '
'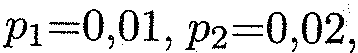
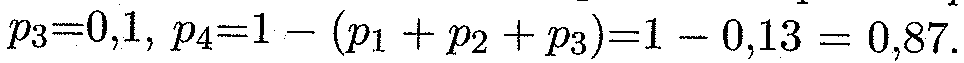 Таким образом искомый закон распределения имеет вид
Таким образом искомый закон распределения имеет вид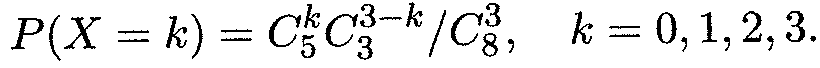
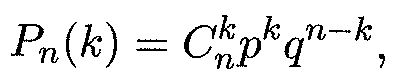 (15.2)
(15.2)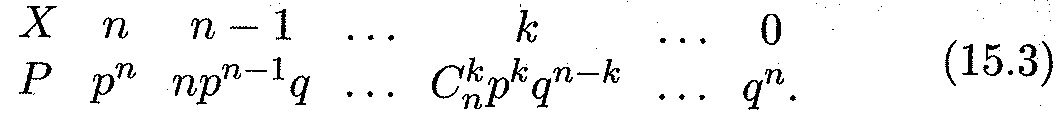
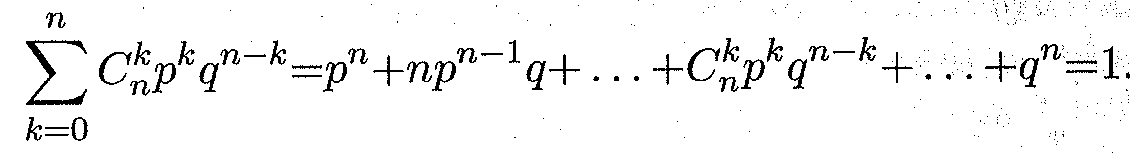
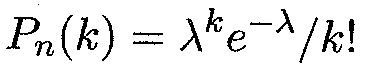 (15.4)
(15.4)