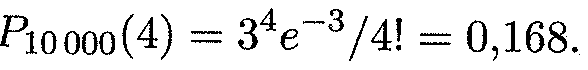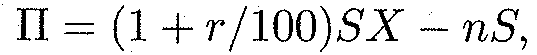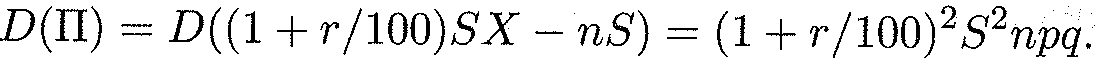Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Случайные события и их классификация.Стр 1 из 6Следующая ⇒
Тема 1.1. Случайные события 1. Случайные события и их классификация. 2. Алгебраические действия над событиями. 3. Элементы комбинаторики. 4. Классическое и статистическое определения вероятности. 5. Формула полной вероятности. Формула Байеса. 6. Повторные независимые испытания. Формула Бернулли. 7. Предельные теоремы в схеме Бернулли (локальная и интегральная теоремы Муавра-Лапласа).
Случайные события и их классификация. Испытание – это комплекс условий появления какого-либо случайного явления. Случайным событием называется такой исход испытания (опыта, эксперимента), который может произойти или не произойти. События обозначаются, как правило, заглавными буквами латинского алфавита A, B, C, D,…. Частота события – отношение числа наступлений события к числу испытаний. Вероятность события – мера объективной возможности появления события.
Классификация событий. Событие называется достоверным, если оно обязательно наступит в результате испытания; достоверное событие обозначается через Событие называется невозможным, если оно заведомо не произойдет в результате испытания; невозможное событие обозначается через Два события называются несовместными, если появление одного из них исключает появление другого события в одном и том же испытании; в противном случае события называются совместными. События A1 , A2, …. An Два события называются независимыми, если вероятности их наступления не зависят от наступления других событий в данном испытании. Несколько событий в данном опыте называются равновозможными, если ни одно из них не является объективно более возможным, чем другие (то есть все события имеют равные «шансы»). События A 1, A 2, …, An образуют полную группу, если они попарно несовместны и в результате каждого опыта происходит одно и только одно из них. Противоположным событию
Элементы комбинаторики. Пусть дано множество, состоящее из n различных элементов. Размещением из n элементов по k
Два размещения различны, если они отличаются друг от друга либо составом элементов, либо порядком их расположения. Число размещений из n элементов по k обозначают символом
где Пример 1. Составить различные размещения по два элемента из элементов множества А={3, 4, 5} и подсчитать их число. Решение. Из трех элементов можно образовать следующие размещения по два элемента:
Пример 2. Сколькими способами 3 награды (за 1-е, 2-е и 3-е места) могут быть распределены между 10 участниками соревнований? Решение. Будем считать, что каждый участник соревнований может получить не более одной награды. Выбрать 3-х участников из 10 можно следующим образом Перестановкой из n элементов называется размещение из n элементов по n элементов. Число перестановок обозначается символом Pn и вычисляется по формуле: Таким образом, указать ту или иную перестановку из n элементов значит выбрать определенный порядок этих элементов. Поэтому любые две перестановки отличаются друг от друга только порядком следования элементов. Пример 3. Сколькими способами можно расставить на книжной полке десятитомник Д. Лондона, располагая их: 1) в произвольном порядке; 2) так, чтобы 1, 5 и 9 тома стояли рядом. Решение. 1) Число способов расстановки 10 книг равно числу перестановок из 10 элементов, то есть 2) Мысленно связав 1, 5 и 9 тома в одну связку, получим 8 «книг», то есть 7 книг и одну связку книг. Их можно расставить на полке Сочетанием из n элементов по k Любые два сочетания отличаются друг от друга хотя бы одним элементом (то есть отличаются только составом элементов). Число сочетаний из n элементов по k обозначается символом
Для чисел
Пример 4. В вазе стоят 9 красных и 7 розовых гвоздик. Сколькими способами можно выбрать из нее: 1) 3 гвоздики; 2) 6 гвоздик одного цвета; 3) 4 красных и 3 розовых гвоздики. Решение. 1) Так как порядок выбора цветов не имеет значения, то выбрать 3 гвоздики из вазы, в которой стоят 16 гвоздик, можно 2) Выбрать 6 гвоздик красного цвета можно 3) Выбрать 4 красных гвоздик из 9 имеющихся можно
.4. Классическое и статистическое определение вероятности. Пусть производится опыт с n равновозможными исходами, образующими полную группу несовместных событий. Такие исходы называются элементарными событиями. Случай, который приводит к наступлению события А, называется благоприятным этому событию. Вероятностью события А называется отношение числа m исходов, благоприятствующих этому событию, к общему числу n исходов:
Из классического определения вероятности следуют следующие свойства: 1) вероятность достоверного события равна единице, то есть все исходы являются благоприятными (m = n): 2) вероятность невозможного события равна нулю (m =0): 3) вероятность случайного события есть положительное число, заключенное между нулем и единицей:
Статистическое определение вероятности связывает понятие вероятности с эмпирическим (опытным) понятием относительной частоты случайного события W (A), которая находится по результатам серии опытов. Относительной частотой случайного события А называется отношение числа опытов, в которых появилось данное событие na, к общему числу фактически произведенных опытов n: Статистической вероятностью события А называется постоянное число, к которому приближаются значения частоты этого события по мере увеличения числа опытов: Пример 5. В городе имеется одиннадцать различных коммерческих банков. Господин «N» открыл по одному счету в пяти различных банках. Позднее четыре банка из одиннадцати изменили ставки процентов по вкладам. Найти вероятность того, что по двум вкладам господина ставки остались неизменными. Решение. Господин выбирал банки случайным образом. Испытание – выбор пяти банков из имеющихся одиннадцати. A – событие, состоящее в том, что по двум вкладам господина, из имеющихся пяти, ставки остались неизменными, и, следовательно, по трем другим изменились.
Таким образом, X 0 1 2 3 Р 0,0179 0,2679 0,5357 0,1785. Пример 3. Вероятностный прогноз для величины X — процентного изменения стоимости акций по отношению к их текущему курсу в течение шести месяцев — дан в виде закона распределения:
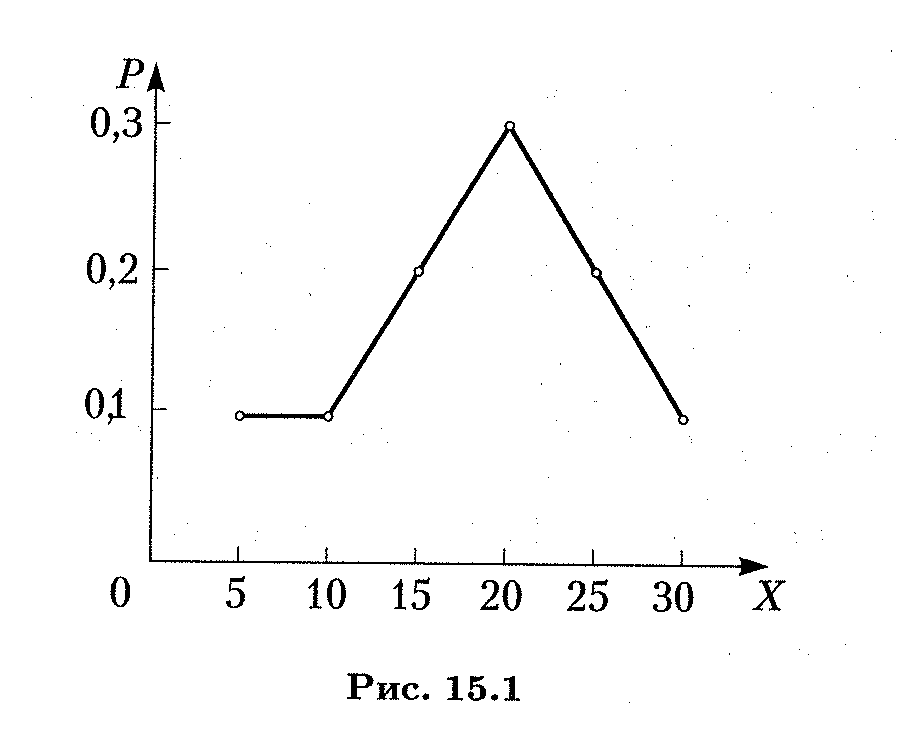
X 5 10 15 20 25 30 Р 0,1 0,1 0,2 0,3 0,2 0,1. Закон распределения дискретной случайной величины можно изобразить графически, соединив в прямоугольной системе координат ХО P точки (х i,р i) отрезками прямых. Так, на рис. 15.1 показан закон распределения из примера 3. Такая фигура называет ся многоугольником распределения.
Биномиальное распределение Пусть производится п независимых испытаний и в каждом из них событие А может либо появиться, либо не появиться. Пусть также вероятность р появления события А в каждом испытании постоянна (см. раздел 14.5). В качестве дискретной случайной величины X рассмотрим число появления события А в этих п испытаниях. Очевидно, что х1 =0, х2=1, х3 =2,..., хп+1=п. Вероятности этих возможных значений к даются формулой Бернулли (см. формулу (14.16)):
где q = 1 - р — вероятность противоположного события (не появление события А в одном испытании). Формула (15.2) представляет собой аналитическую форму закона распределения случайной величины (числа появления события А в п независимых испытаниях), который называется биномиальным. Этот закон получил свое название потому, что правая часть в (15.2) представляет собой общий член разложения бинома Ньютона (14.2). Таким образом, табличная форма биномиального закона с учетом формулы (15.2) имеет вид
Можно показать, что сумма всех вероятностей второй отроки этой таблицы равна единице, т.е.
Пример 4 Банк выдает 5 кредитов. Вероятность невозврата, кредита равна 0,2 для каждого из заемщиков. Составить таблицу закона распределения количества заемщиков, не вернувших кредит по окончании срока кредитования. Решение. Примем за А событие невозврата кредита. Так как заемщики действуют независимо, то выдачу 5 кредитов можно считать за 5 независимых событий. Вероятность невозврата к кредитов из 5 описывается биномиальным распределением (15.2), где р = 0,2, q = 0,8, к принимает значения от нуля до 5. Искомая таблица закона распределения составляется, согласно (15.3), при n = 5: X 5 4 3 2 1 0 Р (0,2)5 5(0,2)40,8 10 (0,2)3(0,8)2 10(0,2)2(0,8)3 5(0,2)(0,8)4 (0,8)5, или окончательно: X 5 4 3 2 1 0 Р 0,00032 0,0064 0,0512 0,2048 0,4096 0,32768.
Распределение Пуассона Пусть в каждом из п производимых испытаний вероятность появления события А равна р. Как мы знаем, для определения вероятности к появлений события А используется формула Бернулли (15.2); при больших п пользуются асимптотической формулой Лапласа (14.17). Однако эта формула плохо подходит для случая, когда р мало. Для случая малых значений р и больших значений п используется асимптотическая формула Пуассона, эта формула выведена при важном допущении, что произведение пр является постоянной величиной, т.е. пр = λ. Тогда вероятность того, что событие А наступит ровно к раз, дается формулой, которая представляет собой закон распределения Пуассона вероятностей массовых и редких (маловероятных) событий.
Пример 5. На базу отправлено 10 000 изделий. Вероятность того, что изделие в пути получит повреждение, равна 0,0003. Найти вероятность того, что на базу прибудут 4 поврежденных изделия. Решение. По условию задачи п = 10 000, р = 0,0003, к = 4. Находим λ, а затем по формуле (15.4) и искомую вероятность:
λ = пр= 10000•0,0003 = 3, Свойства дисперсии Приведем здесь основные свойства дисперсии. Свойство 1. Дисперсия постоянной величины С равна, нулю: D (C) = 0. Свойство 2. Постоянный множитель можно выносить на знак дисперсии, возводя его в квадрат: D (CX) = C 2 D (X). (15.12) Свойство 3. Дисперсия алгебраической суммы независимых случайных величин равна сумме их дисперсий: D (X 1 + X 2 +... + Xn)= D (X 1)+ D (X 2)+... + D (Xn). Перечисленные свойства дисперсии используются при вычислениях, когда мы имеем дело с несколькими случайными величинами. Из свойств 1 и 3 следует важный вывод: D (X + С) = D (X), где С — постоянная величина. Кроме того, справедлива следующая теорема. ТЕОРЕМА 15.2. Дисперсия числа появления события А в п независимых испытаниях с вероятностью появления р в каждом из них этого события вычисляется по формуле D (X) = пр(1 - р) = npq. (15.14) Приведем здесь еще два важных результата: для случайной величины, распределенной по закону Пуассона ( Пример 7. Найти дисперсию числа выигрышных лотерейных билетов, если вероятность выигрыша по одному билету равна 0,015, причем куплено 200 билетов. Поскольку приобретение каждого билета является независимым испытанием относительно появления события А — выпадения выигрыша, то здесь применимы теорема 15.1 и формула (М(Х) = пр. 15.7). В нашем случае п = 200, р = 0,015, откуда мы получаем М (200) = 200 • 0,015 = 3. Решение. Имеем 200 независимых испытаний с вероятностью появления выигрышного билета р = 0,015. Стало быть, q = 1 — 0,015 = 0,985, откуда и получаем искомую дисперсию: D { X) = npq = 200 • 0,015 • 0,985 = 2,955. Пример 8. Банк выдал ссуды п разным заемщикам в размере S р. каждому под ставку ссудного процента r. Найти математическое ожидание и дисперсию прибыли банка, а также условие на ставку ссудного процента, если вероятность возврата ссуды заемщиком равна р. Решение. Поскольку заемщики между собой не связаны, то можно полагать, что мы имеем п независимых испытаний. Вероятность утери ссуды для банка в каждом испытании равна q = 1 —р. Пусть X — число заемщиков, возвративших ссуду с ссудным процентом, тогда прибыль банка определяется формуле
где X является случайной величиной с биномиальным законом распределения. Тогда, согласно теореме 15.1, математическое ожидание прибыли определяется с использованием фор мулы (15.7): М(П) = (1+г/100) SM (X) — nS = (1 + r /100) Snp — Sn = Sn (rp /100 - q). Поскольку выдача ссуды имеет смысл лишь при положительном математическом ожидании прибыли (положительная средняя величина прибыли), то из условия М( П) > 0 вытекает условие на ставку ссудного процента: г > 100 q / p, или г > 100(1 - р)/р. Дисперсия прибыли банка находится, согласно теореме 15.2, с использованием формулы (15.14) и свойств 1-3:
Тема 1.1. Случайные события 1. Случайные события и их классификация. 2. Алгебраические действия над событиями. 3. Элементы комбинаторики. 4. Классическое и статистическое определения вероятности. 5. Формула полной вероятности. Формула Байеса. 6. Повторные независимые испытания. Формула Бернулли. 7. Предельные теоремы в схеме Бернулли (локальная и интегральная теоремы Муавра-Лапласа).
Случайные события и их классификация. Испытание – это комплекс условий появления какого-либо случайного явления. Случайным событием называется такой исход испытания (опыта, эксперимента), который может произойти или не произойти. События обозначаются, как правило, заглавными буквами латинского алфавита A, B, C, D,…. Частота события – отношение числа наступлений события к числу испытаний. Вероятность события – мера объективной возможности появления события.
Классификация событий. Событие называется достоверным, если оно обязательно наступит в результате испытания; достоверное событие обозначается через Событие называется невозможным, если оно заведомо не произойдет в результате испытания; невозможное событие обозначается через Два события называются несовместными, если появление одного из них исключает появление другого события в одном и том же испытании; в противном случае события называются совместными. События A1 , A2, …. An Два события называются независимыми, если вероятности их наступления не зависят от наступления других событий в данном испытании. Несколько событий в данном опыте называются равновозможными, если ни одно из них не является объективно более возможным, чем другие (то есть все события имеют равные «шансы»). События A 1, A 2, …, An образуют полную группу, если они попарно несовместны и в результате каждого опыта происходит одно и только одно из них. Противоположным событию
|
|||||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 439; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.5.68 (0.065 с.) |
 .
. .
. называются попарно-несовместными, если любые два из них несовместны.
называются попарно-несовместными, если любые два из них несовместны.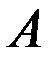 называется событие
называется событие 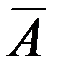 , которое происходит тогда и только тогда, когда не происходит событие
, которое происходит тогда и только тогда, когда не происходит событие 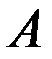 .
.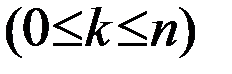 называется любое упорядоченное подмножество данного множества, содержащее k элементов.
называется любое упорядоченное подмножество данного множества, содержащее k элементов.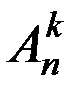 и вычисляют по формуле:
и вычисляют по формуле: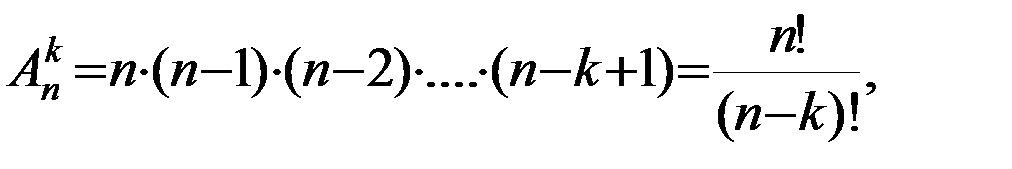
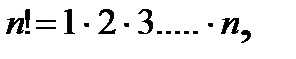 причем
причем 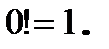
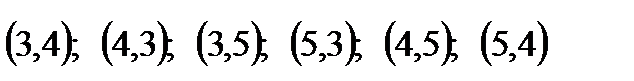 . Таким образом, всего их шесть. Однако число размещений можно посчитать и по формуле (1.1):
. Таким образом, всего их шесть. Однако число размещений можно посчитать и по формуле (1.1):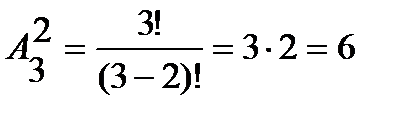 .
.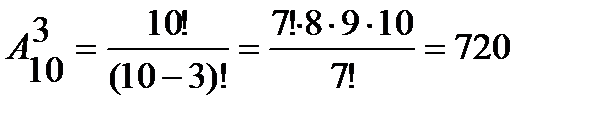 , так как «призовые тройки» отличаются друг от друга либо составом участников, либо порядком их следования.
, так как «призовые тройки» отличаются друг от друга либо составом участников, либо порядком их следования.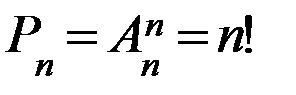
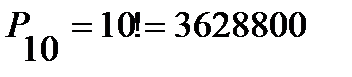 ;
; . Каждому из этих способов расстановки соответствуют
. Каждому из этих способов расстановки соответствуют 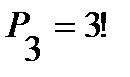 способов расстановки книг, находящихся в связке. Таким образом, число возможных расстановок 10 книг, чтобы три определенные книги стояли рядом (1, 5 и 9) равно:
способов расстановки книг, находящихся в связке. Таким образом, число возможных расстановок 10 книг, чтобы три определенные книги стояли рядом (1, 5 и 9) равно: 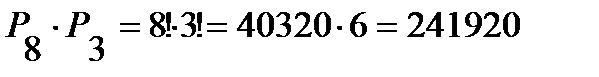 .
.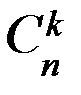 и вычисляется по формуле:
и вычисляется по формуле: 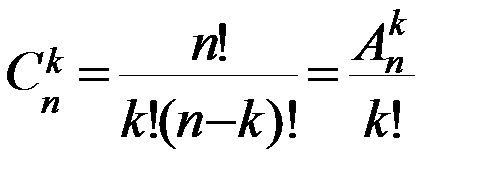
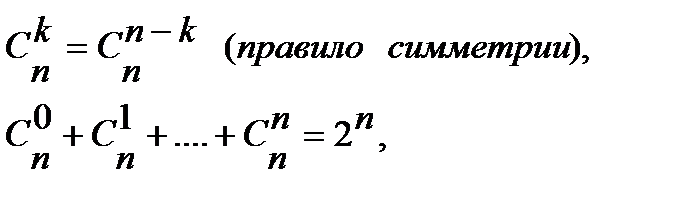
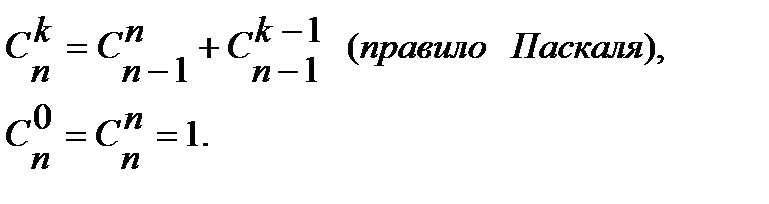
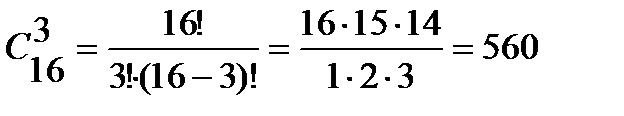 способами;
способами;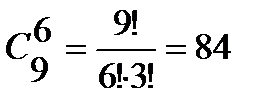 способами, а выбрать 6 гвоздик розового цвета можно
способами, а выбрать 6 гвоздик розового цвета можно  способами. По правилу сложения выбрать 6 гвоздик одного цвета (красных или розовых) можно
способами. По правилу сложения выбрать 6 гвоздик одного цвета (красных или розовых) можно 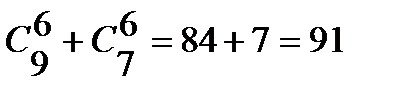 способом;
способом;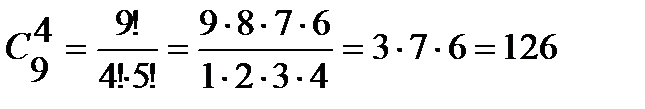 способами, а 3 розовых из имеющихся 7 можно
способами, а 3 розовых из имеющихся 7 можно 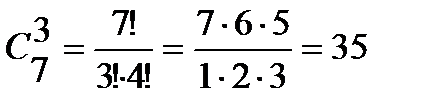 способами. Поэтому букет из 4 красных и 3 розовых гвоздик можно составить по правилу умножения
способами. Поэтому букет из 4 красных и 3 розовых гвоздик можно составить по правилу умножения 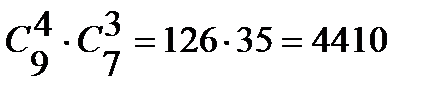 способами.
способами.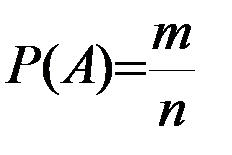
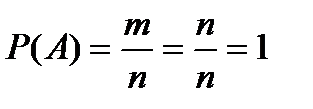 ;
;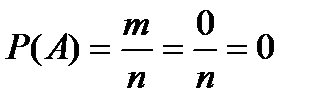 ;
;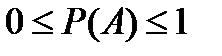 .
.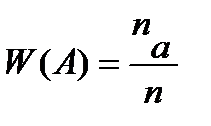 .
.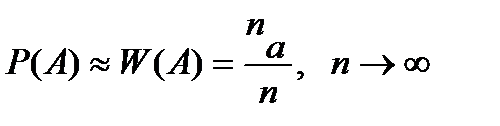
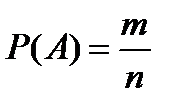 , где
, где 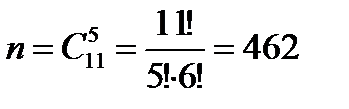 - число всех исходов испытания (несовместимых, единственно возможных и равновозможных);
- число всех исходов испытания (несовместимых, единственно возможных и равновозможных); 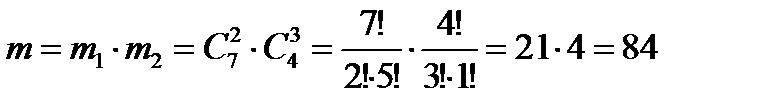 - число исходов, связанных с наступлением события А (
- число исходов, связанных с наступлением события А (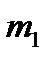 - число вариантов выбора двух банков, из имеющихся семи, не изменивших ставки процентов,
- число вариантов выбора двух банков, из имеющихся семи, не изменивших ставки процентов, 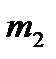 - число вариантов выбора трех банков, из имеющихся четырех, изменивших ставки процентов).
- число вариантов выбора трех банков, из имеющихся четырех, изменивших ставки процентов).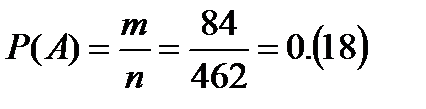 .
.
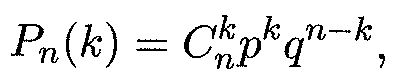 (15.2)
(15.2)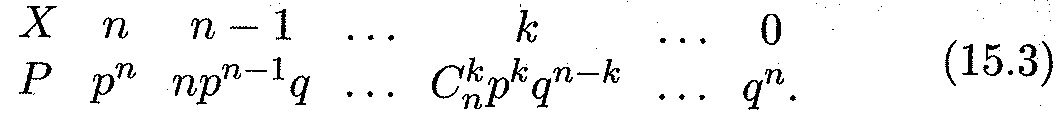
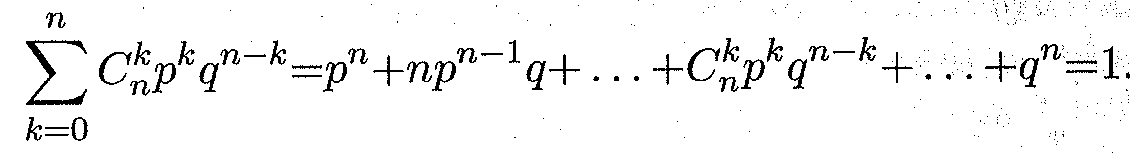
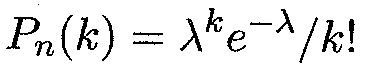 (15.4)
(15.4)