
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Координаты вектора в новом базисе.
Любой вектор можно выразить не только как комбинацию базисных векторов, расположенных на осях, например (1,0) и (0,1), но и как комбинацию какой-то другой линейно-независимой системы.
Задача 72. Доказать, что векторы (1,1) и (1,0) образут базис, и найти координаты вектора (3,2) относительно этого базиса. Решение.
Определитель матрицы перехода, составленной из этих векторов, отличен от 0: Найти новые координаты можно так. Запишем их сначала как неизвестные в векторном равенстве:
Геометрический смысл: вместо того, чтобы 3 раза вправо и 2 раза вверх, можно добраться до точки (3,2) так: 2 раза по диагонали и 1 раз вправо. Ответ. Новые координаты (2,1).
Задача 73. Доказать, что векторы (1,3) и (2,4) образут базис, и найти координаты вектора (1,5) относительно этого базиса. Решение. Вычислим определитель матрицы перехода. Если он не равен 0, то векторы образуют базис.
Составим векторное равенство:
Проверка. 2 способ. Ранее мы находили обратную матрицу для
Решить систему уравнений можно и матричным методом:
Ответ. Новые координаты Задача 74. Даны 3 вектора: Решение. Вычисляя определитель, получим, что он отличен от 0.
Затем ищем новые координаты вектора.
Здесь удобнее сразу же вычесть 2-е уравнение из 3-го, и тогда из последнего определится
Тогда из 1-го уравнения: Ответ. Координаты в новом базисе
Домашняя задача. Доказать, что векторы (2,3) и Ответ. Задача 75. Доказать, что матрица Решение. Сумма квадратов элементов каждого столбца равняется
Зелёным отмечены векторы старого базиса, красным - нового. При их суммировании мы как раз и попадаем в точку Ответ. (1,1). Задача 76. Доказать, что матрица Решение. Сумма квадратов элементов каждого столбца равна Скалярное произведение разных столбцов равно
Практика 9 Элементы векторной алгебры. Таблица свойств скалярного и векторного произведений.
Задача 77. Найти скалярное и векторное произведение векторов (1,1,1) и (1,2,3). Решение. Скалярное Векторное Ответ. Скалярное 6, векторное (1,-2,1). Замечание. Можно проверить, что (1,-2,1) перпендикулярен исходным векторам (скалярно умножить на 1-й или на 2-й вектор, получим 0). Задача 78. Найти скалярное и векторное произведение векторов:
Решение. Для поиска векторого произведения запишем определитель.
Ответ. Скалярное: 16, векторное: (-13, -1, -8).
Задача 79. Найти косинус угла между векторами Решение. учитывая что Заметим, что Ответ. Задача 80. Найти косинус угла между векторами Решение. учитывая что Оценим приблизительно, какой это угол. Заметим, что если было бы В данном случае косинус чуть меньше, а значит угол чуть больше 600. Ответ.
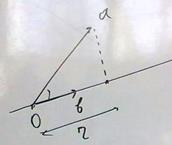
Задача 81. Вывести формулу проекции вектора на ось Решение. 1) известно, что 2) длина проекции
Сопоставим эти 2 факта.
Задача 82. Найти проекцию вектора Решение. По формуле Ответ.
Задача 83. Доказать неравенство Коши-Буняковского: Решение. Рассмотрим скалярное произведение
А теперь рассмотрим это выражение как неравенство с квадратичным трёхчленом относительно переменной
Извлечём корень и получим
Задачи 84 и 85. Векторы a,b выражены через p,r: № 84. Найти Решение № 84. Так как
Ответ. 12. Решение № 85. | [a,b] | =
Ответ. Задача 86. Дано: Решение. Примечание. Как видим, можно вычислять скалярное произведение, даже не зная координат векторов. Здесь фактически
Пункт Б.
Ответ.
Задачи 87,88,89. Векторы a,b выражены через p,r: Задача 87. Найти Задача 88. Найти | [a,b] |. Задача 89. Найти Решение задачи 87.
Мы раскрыли скобки, используя свойства скалярного произведения. Далее, так как Это можно выразить так:
Ответ. 29. Решение задачи 88.
Несмотря на то, что скобки мы раскрыли похожим образом, дальше будет существенное отличие, т.к. свойства векторного произведения совсем другие, чем скалярного. Так,
Решение задачи 89.
Практика № 10. Задача 90. Вычислить площадь параллелограмма, образованного векторами Решение. Площадь параллелограмма - значит, надо вычислить модуль векторного произведения
Ответ 92.
Задачи 91 и 92. Векторы a,b выражены через p,q: Задача 91. Найти Решение.
Ответ. 1227. Задача 92. Найти | [a,b] |. Решение. | [a,b] | = |
Ответ.
Задача 93. Найти смешанное произведение трёх векторов:
Решение. Вычислим определитель:
Задача 94. Доказать, что 4 точки: A(1,1,1), B(2,3,1), C(2,4,2), D(3,6,2) лежат в одной плоскости. Решение. Составим 3 вектора AB, AC, AD и докажем, что они лежат в одной плоскости. AB = (1,2,0), AC = (1,3,1), AD = (2,5,1). Определитель Ответ. 4 точки в одной плоскости. Задача 95. Найти объём тетраэдра, вершины которого
A(1,1,1), B(2,1,3), C(2,2,4), D(1,2,4). Решение. Объём тетраэдра ровно в 6 раз меньше объёма параллелепипеда с рёбрами AB, AC, AD. Найдём эти векторы, и сначала вычислим объём параллелепипеда с помощью определителя, затем поделим на 6. AB = (1,0,2), AC = (0,1,3), AD = (1,1,3).
Ответ. Объём тетраэдра равен
Линейные операторы Задача 96. Построить матрицу линейного оператора в 2-мерном пространстве, если действие оператора задано таким образом: Решение. Находим, в какие векторы отображаются два базисных вектора: Эти результаты запишем по столбцам: Ответ. Матрица линейного оператора Проверка: Так,
Задача 97. Построить матрицу линейного оператора в 3-мерном пространстве Решение. Отобразим базис 3-мерного пространства.
Ответ. Матрица линейного оператора
Задача 98. Построить матрицу оператора поворота на произвольный угол Решение. Найдём матрицу оператора поворота на угол
Расстояния r1 и r2 здесь равны Ответ. При При
Задача 99. С помощью линейного оператора поворота плоскости доказать, что скалярное произведение не изменяется при повороте. Решение. Рассмотрим векторы
А теперь скалярно перемножим 2 получившихся вектора:
Учитывая, что 3,4,7,8 слагаемые взаимоуничтожаются, получим:
Ответ: Что и требовалось доказать.
Практика 11 (21.10.2020).
|
|||||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 1282; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.189.177 (0.095 с.) |

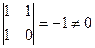 .
. 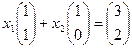 это очевидно, преобразуется к системе:
это очевидно, преобразуется к системе: 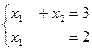 . , её решение:
. , её решение: 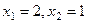 .
. 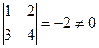 .
.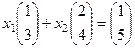 , оно сводится к системе уравнений.
, оно сводится к системе уравнений.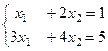 . Можно решить её как методом Гаусса, так и матричным методом.
. Можно решить её как методом Гаусса, так и матричным методом.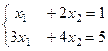


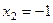
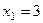 . Новые координаты
. Новые координаты  .
. 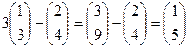
 .,
., 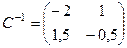 .
.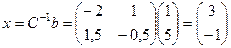 .
. 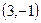 .
. 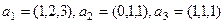 . Доказать, что они образуют базис в пространстве, и найти новые координаты вектора
. Доказать, что они образуют базис в пространстве, и найти новые координаты вектора 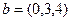 .
.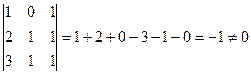 .
. 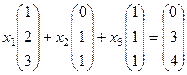 система:
система: 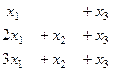

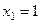 .
.
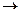
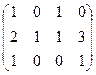 .
. , а тогда из 2-го
, а тогда из 2-го 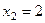 .
.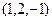 .
. образут базис, и найти координаты вектора (1,0) относительно этого базиса.
образут базис, и найти координаты вектора (1,0) относительно этого базиса.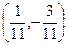 .
.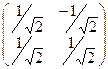 является ортогональной матрицей, и найти кооринаты вектора
является ортогональной матрицей, и найти кооринаты вектора 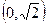 в базисе, соответствующем этой матрице перехода.
в базисе, соответствующем этой матрице перехода. , скалярное произведение различных столбцов 0. Поэтому матрица является матрицей перехода от одного ортонормированного базиса к другому ортонормированному базису. Такие матрицы отличаются важным свойством: обратная матрица совпадает с транспонированной. Поэтому для поиска новых координат умножим транспонированную матрицу на
, скалярное произведение различных столбцов 0. Поэтому матрица является матрицей перехода от одного ортонормированного базиса к другому ортонормированному базису. Такие матрицы отличаются важным свойством: обратная матрица совпадает с транспонированной. Поэтому для поиска новых координат умножим транспонированную матрицу на 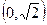 .
. 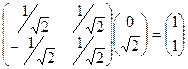

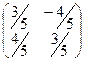 является ортогональной.
является ортогональной. 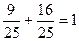 .
.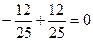 .
.
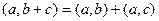
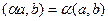
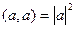

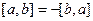
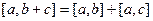

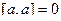
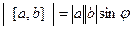
 .
. 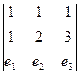 =
= 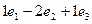 =
= 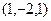 .
.  и
и 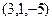 .
.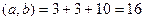 .
.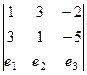 =
= 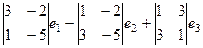 =
= 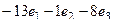 .
.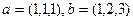 .
. 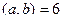 ,
, 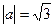 ,
, 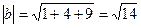 ,
,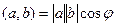 , то
, то 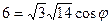
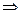
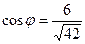 .
.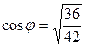 , т.е. чуть меньше 1, угол близок к 0.
, т.е. чуть меньше 1, угол близок к 0.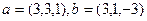 .
. 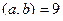 ,
,  ,
, 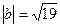 ,
,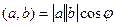 , то
, то 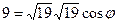
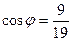 .
. то было бы
то было бы 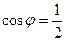 и угол 600.
и угол 600.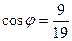 .
.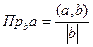 .
.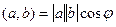 .
.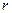 это катет,
это катет, 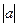 гипотенуза треугольника, тогда получается, что
гипотенуза треугольника, тогда получается, что 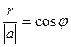 .
.
 , тогда
, тогда 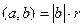 , откуда и следует
, откуда и следует 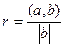 .
. 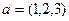 на линию, порождаемую вектором
на линию, порождаемую вектором 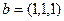 .
.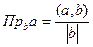 =
= 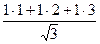 =
= 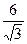 =
=  =
= 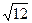 . Кстати, длина самого вектора
. Кстати, длина самого вектора 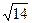 , соотв-но длина проекции чуть меньше.
, соотв-но длина проекции чуть меньше.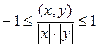 .
.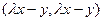 . Так как здесь умножается один и тот же вектор на себя, то оно неотрицательно:
. Так как здесь умножается один и тот же вектор на себя, то оно неотрицательно: 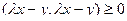 . По свойствам скалярного произведения, раскроем скобки:
. По свойствам скалярного произведения, раскроем скобки: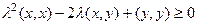
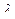 . Для каждых конкретных векторов
. Для каждых конкретных векторов 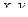 то это неравенство приобретает вид:
то это неравенство приобретает вид:  , где
, где 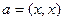 ,
, 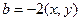
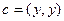 . Если выражение больше ири равно 0, то значит, для самого квадратичного уравнения нет корней или всего 1 корень, но не 2 корня. То есть, дискриминант меньше или равен 0. Тогда
. Если выражение больше ири равно 0, то значит, для самого квадратичного уравнения нет корней или всего 1 корень, но не 2 корня. То есть, дискриминант меньше или равен 0. Тогда  =
= 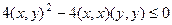 , тогда
, тогда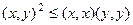

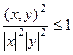 .
.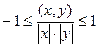 .
.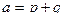 ,
, 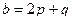 .
. 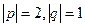 , угол между ними 60 градусов.
, угол между ними 60 градусов.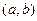 . № 85. Найти | [a,b] |.
. № 85. Найти | [a,b] |.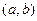 =
=  =
= 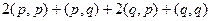
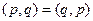 для скалярного произведения, то получаем
для скалярного произведения, то получаем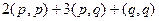 =
= 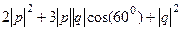 =
= = 8+3+1 = 12.
= 8+3+1 = 12.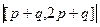 раскрытие скобок идёт так же, как и для скалярного произведения, но затем будут применяться другие свойества. Так, при смене мест надо будет поменять знак, а векторное произведение двух одинаковых векторов равно 0, а не квадрату модуля.
раскрытие скобок идёт так же, как и для скалярного произведения, но затем будут применяться другие свойества. Так, при смене мест надо будет поменять знак, а векторное произведение двух одинаковых векторов равно 0, а не квадрату модуля. =
= 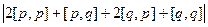 =
= 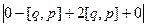 =
= 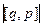 =
= 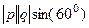 =
=  =
= 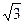 .
.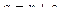 ,
,  ,
, 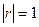 ,
,  , угол между векторами
, угол между векторами 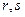 45 градусов. Найти
45 градусов. Найти 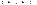 и
и 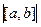 .
. =
= 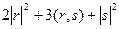 =
= 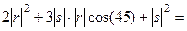
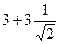 .
.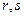 служат в качестве базисных векторов, и через них выражены
служат в качестве базисных векторов, и через них выражены 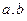 , то есть (1,1) и (2,1) координаты
, то есть (1,1) и (2,1) координаты  относительно базиса
относительно базиса 
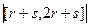 =
= 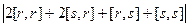 =
= =
= 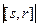 =
= 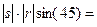
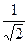 .
.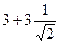 и
и 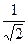 .
.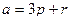 ,
, 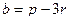 .
. 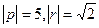 , угол между ними 45 град.
, угол между ними 45 град.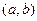 .
. 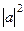 .
.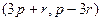 =
= 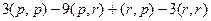 .
.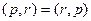 то объединим их, и получим
то объединим их, и получим 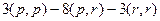 .
.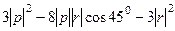 и получаем
и получаем 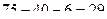 .
. =
= 
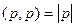 , но
, но 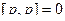 . Кроме того, чтобы объединить
. Кроме того, чтобы объединить 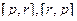 в одно слагаемое, здесь надо сначала у одной из них сменить знак.
в одно слагаемое, здесь надо сначала у одной из них сменить знак.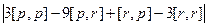 =
= 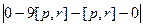 =
=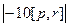 =
= 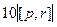 . Модуль векторного произведения
. Модуль векторного произведения  и
и 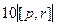 =
= 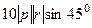 =
= 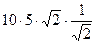 = 50. Ответ. 50.
= 50. Ответ. 50.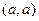 =
=  =
=  =
= =
= 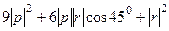 =
=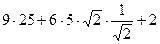 =
=  = 257. Ответ. 257.
= 257. Ответ. 257.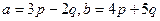 ,
,  , угол между p,q равен
, угол между p,q равен 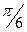 .
. 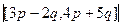 =
=  =
=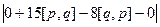 =
= 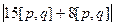 =
= 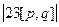 =
= 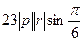 =
=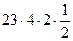 = 92.
= 92.  ,
, 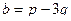 .
. 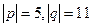 , угол между ними 600.
, угол между ними 600.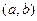 .
. 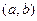 =
= 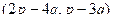 =
= 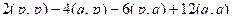 =
= 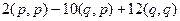 =
=  =
= =
= 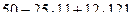 = 1227.
= 1227.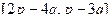 |= |
|= |  | = |
| = | 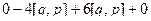 | = |
| = | 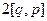 | =
| =  =
=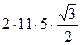 =
= 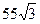 .
.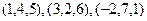 .
. =
=  = 25. Ответ.
= 25. Ответ. 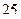 .
. = 0 так как 3 строка есть сумма 1-й и 2-й.
= 0 так как 3 строка есть сумма 1-й и 2-й. =
=  ,
, 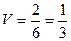 .
.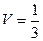 .
. .
.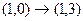 ,
, 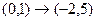 .
. .
. . То есть действительно, вычисление координат образа вектора по данным формулам даёт точно такой же результат, как и с помощью умножения на матрицу.
. То есть действительно, вычисление координат образа вектора по данным формулам даёт точно такой же результат, как и с помощью умножения на матрицу.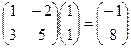 но ведь и по исходным формулам
но ведь и по исходным формулам  получилось бы то же самое:
получилось бы то же самое: 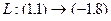 .
.
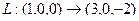
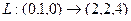
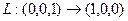
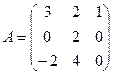 .
. .
.
 и
и  . Красным показаны образы базисных векторов. Получаем матрицу
. Красным показаны образы базисных векторов. Получаем матрицу 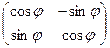 .
. получится
получится  Действие оператора на любой вектор задаётся матрицей так:
Действие оператора на любой вектор задаётся матрицей так: 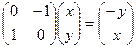 - любой вектор поворачивается на 90 градусов.
- любой вектор поворачивается на 90 градусов.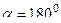 матрица
матрица 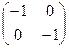 , и действительно, умножение на такую матрицу переводит любой вектор
, и действительно, умножение на такую матрицу переводит любой вектор 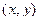 в
в  .
.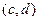 . Их скалярное произведение равно
. Их скалярное произведение равно 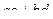 . теперь отобразим каждый из этих векторов с помощью линейного оператора поворота на угол
. теперь отобразим каждый из этих векторов с помощью линейного оператора поворота на угол 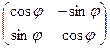
 =
= 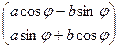
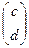 =
= 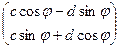
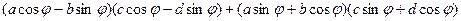 =
=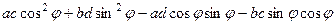 +
+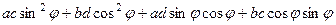
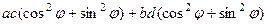 =
= 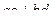 .
.


