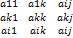Ранг матрицы, теоремы о ранге.

Выберем в матрице А =aij размерности m n произвольные к строк и к столбцов, где 1 ≤ к ≤ min {m, n}. Определитель к-го порядка, составленный из элементов этой матрицы, расположенных на пересечении выделенных к строк и к столбцов, называется минором Мк к-го порядка матрицы А.

Минорами первого порядка являются сами элементы матрицы А, а их число равно mn. Если матрица нулевая, то все ее возможные миноры равны нулю.

Если все миноры некоторого порядка данной матрицы А равны нулю, то равны нулю и все миноры более высоких порядков.

Рангом матрицы называется наивысший порядок отличных от нуля миноров, то данное определение не позволяет говорить о ее ранге. По определению полагают, что ранг нулевой матрицы равен нулю. Если матрица имеет хотя бы один отличный от нуля элемент, то r ≥ 1. Тогда ясно, что только нулевая матрица имеет ранг, равный нулю.

Пусть Мк – главный (угловой) минор матрицы А порядка к. Любой минор (к + 1)-го порядка вида

М (k+1)=

получающийся из Мк добавлением элементов i-й строки и j-го столбца, называется окаймляющим для минора Мк.

Справедлива теорема: если какой-нибудь угловой минор r-го порядка матрицы А отличен от нуля, а все миноры (r + 1)-го порядка, его окаймляющие, равны нулю, то ранг матрицы равен r. Из этой теоремы получаем следующий способ вычисления ранга матрицы: при вычислении ранга следует переходить от миноров меньших порядков к минорам высших порядков; если при этом окажется, что какой-то минор Мr отличен от нуля, а все окаймляющие миноры Мк+1 равны нулю, то ранг матрицы равен r.

Элементарными преобразованиями матрицы называются следующие преобразования:

1) перестановка местами любых двух строк;

2) умножение любой строки на произвольное отличное от нуля число;

3) прибавление к любой строке всякой другой строки, умноженное на не- которое число;

4) аналогичные преобразования столбцов матрицы.

Справедлива теорема: при элементарных преобразованиях матрицы ее ранг не изменяется. Тогда при вычислении ранга матрицы можно исключить из рассмотрения (вычеркнуть, отбросить):

1) нулевые строки;

2) одну из двух равных строк;

3) одну из двух пропорциональных строк;

4) строку, являющуюся линейной комбинацией остальных строк.

Обычно, отбрасывая нулевые строки и столбцы, матрицу А = (аij) приводят к трапецоидальной форме или треугольной форме, если все элементы b11, b22, …, brr этих двух матриц отличны от нуля, то их ранги равны числу r.

 

Критерий совместности системы(теорема Кронекера-Капелли).

Под расширенной матрицей системы будем понимать матрицу, включающую в себя столбец свободных членов (после черты). В результате элементарных преобразований строк расширенная матрица приводится к одному из трех случаев:

В первом случае система имеет единственное решение.

Во втором случае система уравнений имеет бесконечное множество решений и в третьем она несовместна.

Установить, совместна ли система

или несовместна (без нахождения ее решений) позволяет теорема Кронекера-Капелли: необходимым и достаточным условием совместности системы (1) является условие равенства рангов матрицы А системы и расширенной матрицы А(с черт): 

r(A) = r(Ас черт).

Так как теорема дает необходимое и достаточное условие совместности системы, то ее называют критерием совместности системы линейных уравнений.

Заметим, что либо r(А с черт) = r(A), либо r(А счерт) = r(A) + 1. Если r(А с черт) > r(A), то система (1) противоречива.

1) если ранг матрицы системы равен рангу расширенной матрицы и равен числу неизвестных, то система имеет единственное решение;

2) если ранг матрицы системы равен рангу расширенной матрицы, но меньше числа неизвестных, то система имеет бесконечное множество решений.

Если ранг матрицы системы меньше ранга расширенной матрицы, то система несовместна и решения не существует.