Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование систем методом Гаусса.
-метод последовательного исключения неизвестных. Предположим, что в системе
какой-нибудь коэффициент при х1 отличен от нуля. Без ограничения общности можно считать, что а11≠ 0. В этом случае коэффициент а11 называется разрешающим или ведущим элементом. Первое уравнение называется разрешающим, а первый столбец – разрешающим столбцом. При первой шаге из всех последующих уравнений исключается неизвестной х1. Далее, если во втором уравнении а22*≠ 0, то этот элемент объявляем разрешающим. Выполняем действия второго этапа. Первое и второе уравнения преобразованной системы оставляем неизменными. У всех остальных уравнений исключаем неизвестное х2. И так далее.
Здесь а11, а22*, …, аrr* не равны нулю. При этом r ≤ m и r ≤ n. Переход от системы (1) к системе (2) называют прямым ходом метода Гаусса. Систему линейных уравнений вида (2) называют ступенчатой системой. Если r<n, то она имеет трапецоидальный вид. Если r = n, то получим следующую треугольную систему:
Матрица системы (3) имеет треугольный вид (при этом а11 ≠ 0, а22* ≠ 0, …, аrr* ≠ 0). Пусть r = n, т.е. преобразованная система имеет треугольную форму (3). Тогда система (1) совместна и определенна. Единственное решение этой системы находится следующим образом. Из последнего уравнения находим вполне определенное значение хn: xn = Подставляя это хn в предпоследнее уравнение системы (3), найдем конкретное значение хn – 1. Пусть теперь r < n, т.е. система имеет трапецоидальный вид. Тогда она имеет бесконечное множество решений В общем случае разрешающим может быть любой элемент ask ≠ 0. Тогда к системам вида (2) или (3) можно перейти лишь после надлежащего изменения нумерации неизвестных и уравнений. Для нахождения же самого решения исходной системы эта нумерация не нужна. Однородная система треугольного вида всегда совместна. Если в посл системе m < n, то помимо очевидного (тривиального) решения, она имеет бесчисленное множество ненулевых решений. Если m = n, то решение либо единственно (это нулевое решение), либо их бесчисленное множество.
Метод Крамера Система линейных алгебраических уравнений называется крамеровской, если число m уравнений совпадает с числом n неизвестных и определитель ∆(А) квадратной матрицы А данной системы отличен от нуля. Определитель ∆(А), называемый определителем системы, имеет вид
Каждая крамеровская система линейных уравнений совместна и определенна, т.е. имеет единственное решение, которое определяется формулами Крамера
x1 =
Здесь Δj (j = 1, …, n) есть определитель, получающийся из определителя (1) системы путем замены его j – го столбца столбцом из свободных членов система. Если Δ = 0 и хотя бы один из определителей Δj не равен нулю, то система не совместна. Если Δ = 0 и все определители Δj равны нулю, то система может быть совместной (тогда она имеет бесконечно много различных решений) или несовместной. Для решения системы трех линейных уравнений с тремя неизвестными методом Крамера нужно вычислить определители Δ,Δ x1, Δ x2, Δ x3, где Δ – определитель, составленный из коэффициентов при неизвестных, Δ x1, Δ x2, Δ x3 получены из Δ заменой столбцов коэффициентов при x1, x2, x3 соответственно на столбец свободных членов. При этом, если 1) Δ не= 0, система имеет единственное решение 2) Δ = Δ x1= Δ x2= Δ x3=0, система несовместна или имеет бесконечное множество решений; 3) Δ =0 и хотя бы один из Δ x1, Δ x2, Δ x3 отличен от нуля, система несовместна.
|
|||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 58; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.218.184 (0.004 с.) |
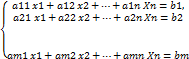
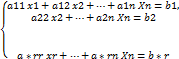
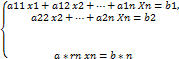
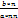 (a*nn≠0)
(a*nn≠0)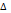 =
=  (1)
(1)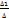 ,…,xj=
,…,xj= 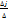 ,…,xn=
,…,xn=