
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение вектора, его длины. Равные и противоположные векторы. Сложение и вычитание векторов. Умножение вектора на число.
Рассмотрим произвольный отрезок. На нем можно указать два направления: от одного конца к другому и наоборот. Чтобы выбрать одно из направлений, один конец отрезка назовем началом, а другой – концом и будем считать, что отрезок направлен от начала к концу. ® В Конец вектора А Вектором, или направленным отрезком, Начало вектора называется отрезок вместе с его направлением.
На рисунках вектор изображается отрезком со стрелкой, показывающей направление вектора. Векторы обозначают двумя заглавными латинскими буквами со стрелкой над ними, например Любая точка плоскости также является вектором. В этом случае вектор называется нулевым. Начало нулевого вектора совпадает с его концом, а на рисунке такой вектор изображается одной точкой. Если, например, точка, изображающая нулевой вектор, обозначена буквой М, то данный нулевой вектор можно обозначить Длиной или модулем ненулевого вектора Ненулевые векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых; нулевой вектор считается коллинеарным любому вектору.
· М A · D E C
Векторы Если два ненулевых вектора
Два ненулевых вектора, лежащие на параллельных прямых, называются сонаправленными (противоположно направленными) если их концы лежат по одну сторону (по разные стороны) от прямой, проходящей через начала. Если векторы Начало нулевого вектора совпадает с его концом, поэтому нулевой вектор не имеет какого-либо определенного направления. Иначе говоря, любое направление можно считать направлением нулевого вектора. Условимся считать, что нулевой вектор сонаправлен с любым вектором. Ненулевые коллинеарные векторы обладают следующими свойствами:
Векторы называются равными, если они сонаправлены и их длины равны.
Пусть равный A C Вектор Суммой векторов Это правило сложения векторов называется правилом треугольника. Cправедливо равенство Правило треугольника можно сформулировать также следующим образом: если А, В и С – произвольные точки, то Рассмотрим свойства сложения векторов. Теорема. Для любых векторов
1. 2. ( Доказательство. 1. Рассмотрим случай, когда векторы B 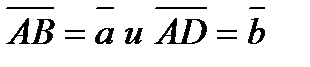 и на этих векторах построим и на этих векторах построим
параллелограмм ABCD. По правилу треугольника А
B вектор Применяя правило треугольника, получим: A D
( Þ ( При доказательстве свойства 1 мы обосновали так называемое правилопараллелограмма сложения неколлинеарных векторов: чтобы сложить неколлинеарные векторы Сложение нескольких векторов производится следующим образом: первый вектор складывается со вторым, затем их сумма складывается с третьим вектором и т.д. Из закона сложения векторов следует, что сумма нескольких векторов не зависит от того, в каком порядке они складываются. угольника.
образом: если А1, А2, …, Аn -
Это равенство справедливо для любых точек А1, А2, …, Аn, в частности, в том случае, когда некоторые из них совпадают. Например, если начало первого совпадает с концом последнего вектора, то сумма данных векторов равна нулевому вектору. Разностью векторов Разность векторов Рассмотрим задачу о построении разности двух векторов. Задача. Даны векторы Решение. А Отметим на плоскости произвольную точку О и
отложим от этой точки векторы О По определению разности векторов это означает, что Введем понятие вектора, противоположного данному. В Пусть
Вектор Вектор, противоположный вектору Очевидно, Теорема. Для любых векторов Доказательство. По определению разности векторов ( ( Отметим на плоскости произвольную точку О и отложим от этой точки вектор
- разности векторов Произведение вектора
- 2
Из определения произведения вектора на число следует, что: 1) произведение любого вектора на число нуль есть нулевой вектор; 2) для любого числа k и любого вектора
 , , 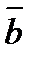 справедливы равенства: справедливы равенства:
Доказательство. Если k ¹ 0, l ¹ 0, 2)
О k Если сумма k + l > 0, то векторы (k + l)
Если (k + l) < 0, то (-k – l) > 0 и, по доказанному, (-k - l) Откуда умножением на (-1) получаем (k + l) А 3) А1
О
D ОАВ ~ D ОА1В1 с коэффициентом подобия k, поэтому
|
|||||||||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 142; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.243.184 (0.067 с.) |
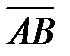 . Первая буква обозначает начало вектора, вторая – конец. Векторы часто обозначают и одной латинской буквой со стрелкой над ней:
. Первая буква обозначает начало вектора, вторая – конец. Векторы часто обозначают и одной латинской буквой со стрелкой над ней: 
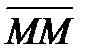 . Нулевой вектор обозначается символом
. Нулевой вектор обозначается символом 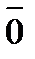 .
. . Длина нулевого вектора считается равной нулю:
. Длина нулевого вектора считается равной нулю: 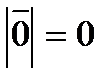 .
.
 (вектор
(вектор  нулевой) коллинеарные, а векторы
нулевой) коллинеарные, а векторы 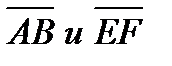 , а также
, а также  не коллинеарны.
не коллинеарны.
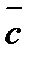





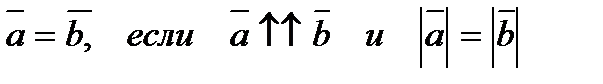
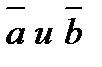 - два вектора. Отметим произвольную
- два вектора. Отметим произвольную , равный
, равный  .
. называется суммой векторов
называется суммой векторов 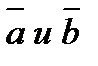 . Сумма векторов
. Сумма векторов 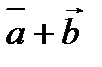
 .
.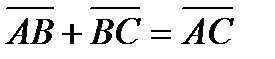 . Это равенство справедливо для произвольных точек А, В и С, в частности, в том случаае, когда две из них или все три совпадают.
. Это равенство справедливо для произвольных точек А, В и С, в частности, в том случаае, когда две из них или все три совпадают. ,
, 
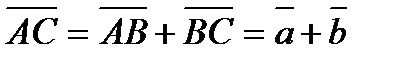 . Аналогично
. Аналогично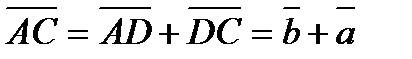 . Отсюда следует, что
. Отсюда следует, что 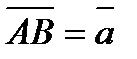 , от точки В – вектор
, от точки В – вектор  ,
,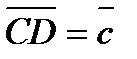 .
.
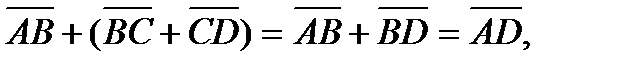
 и
и  и построить параллелограмм ABCD. Тогда вектор
и построить параллелограмм ABCD. Тогда вектор  равен
равен 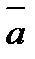 +
+  Правило построения суммы нескольких
Правило построения суммы нескольких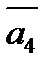
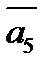 векторов называется правилом много -
векторов называется правилом много -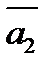 Правило многоугольника можно
Правило многоугольника можно 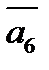 сформулировать также следующим
сформулировать также следующим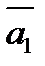
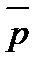 произвольные точки плоскости, то
произвольные точки плоскости, то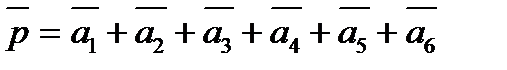
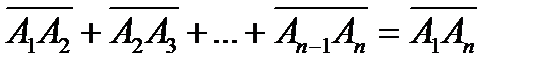 .
.
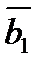 +
+ 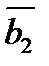 +
+  +
+  =
= 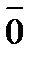
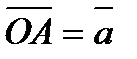 и
и 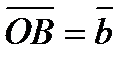 .
. -
- 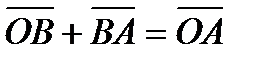 , или
, или . Таким образом, сумма векторов
. Таким образом, сумма векторов  и
и  , т.е. вектор
, т.е. вектор  Вектор
Вектор  .
.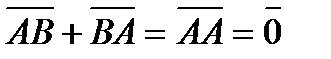
 -
- 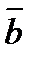 =
= 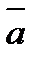 -
-  . Прибавив к обеим частям этого равенства вектор (-
. Прибавив к обеим частям этого равенства вектор (-  -
-  -
- 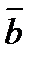 =
= 
 По теореме о
По теореме о -
-  =
= 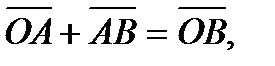 т.е. вектор
т.е. вектор 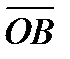 искомый.
искомый. , причем векторы
, причем векторы  на число k обозначается так: k
на число k обозначается так: k 
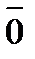 , то оба вектора (k l)
, то оба вектора (k l)  , и одно и то же направление. Это направление такое же, как и у
, и одно и то же направление. Это направление такое же, как и у 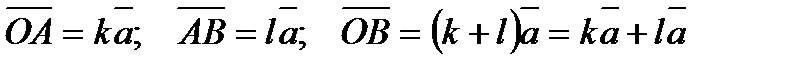
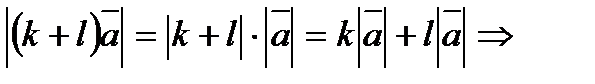 (k + l)
(k + l) 

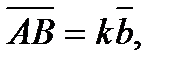
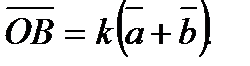 . С другой стороны,
. С другой стороны, 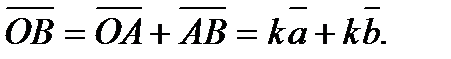 Таким образом, k(
Таким образом, k(


